Với giải Câu hỏi trang 73 Toán 10 Tập 2 Chân trời sáng tạo trong Bài tập cuối chương 9 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Chân trời sáng tạo trang 73 Bài tập cuối chương 9

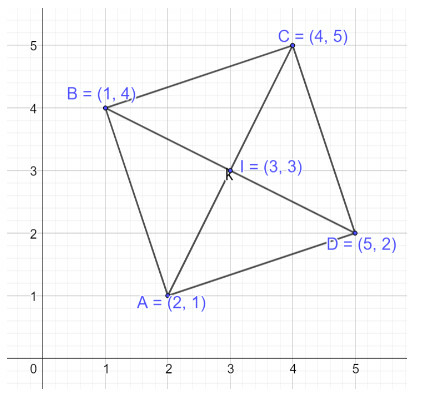
Bài 1 trang 73 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho bốn điểm $A(2;1),B(1;4),C(4;5),D(5;2)$

a) Chứng minh ABCD là một hình vuông

b) Tìm tọa độ tâm I của hình vuông ABCD

Phương pháp giải

a)       Bước 1: Tính AB, BC, CD, DA (Chứng minh AB=BC=CD=DA)

          Bước 2: Chứng minh $AB\mathrm{\perp }BC$ thông qua tích vô hướng

b) Sử dụng tính chất trung điểm $M\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)$ với M là trung điểm của AB

Lời giải 

a) Ta có: $\overrightarrow{AB}=(-1;3),\overrightarrow{BC}=(3;1),\overrightarrow{CD}=(1;-3),\overrightarrow{DA}=(-3;-1)$

Suy ra $AB=BC=CD=DA=\sqrt{10}$

Mặt khác $\overrightarrow{AB}.\overrightarrow{BC}=(-1).3+3.1=0\Rightarrow AB\mathrm{\perp }BC$

Vậy ABCD là hình vuông

b) Ta có ABCD là hình vuông, nên tâm I là trung điểm của đoạn thẳng AC

Vậy tọa độ điểm I là $I(3;3)$

Bài 2 trang 73 Toán 10 Tập 2: Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB

Phương pháp giải

Bước 1: Xét với đường tròn bất kì, cho tọa độ các điểm A, B, C, D

Bước 2: Xác định tọa độ điểm E, F

Bước 3: Tính $\overrightarrow{EF}.\overrightarrow{DB}$, suy ra vuông góc

Lời giải 

Xét với đường tròn (O) có phương trình $(O):{\left(x-3\right)}^2+{\left(y-4\right)}^2=25$

Cho các điểm $A(0;0),B(0;8),C(8;4),D(-2;4)$ nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD

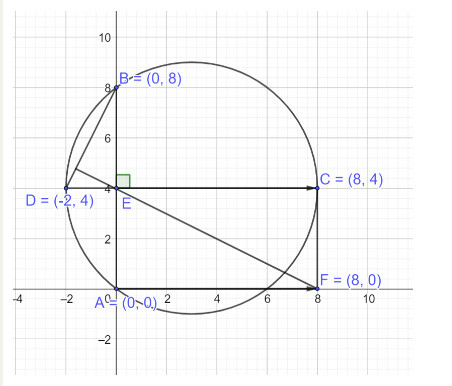
Phương trình đường thẳng đi qua hai điểm A, B có dạng $x=0$

Phương trình đường thẳng đi qua hai điểm C, D có dạng $y=4$

Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau:

$\{\begin{array}{l}x=0\\ y=4\end{array}\iff E(0;4)$

Gọi tọa độ của điểm F là: $F(x;y)$

ACEF là hình chữ nhật nên $\overrightarrow{AF}=\overrightarrow{EC}$, mặt khác ta có: $\overrightarrow{AF}=(x;y),\overrightarrow{EC}=\left(8;0\right)$

Suy ra tọa độ điểm F là: $F\left(8;0\right)$

$\overrightarrow{EF}=\left(8;-4\right),\overrightarrow{DB}=\left(2;4\right)\Rightarrow \overrightarrow{EF}.\overrightarrow{BD}=8.2+\left(-4\right).4=0\Rightarrow \overrightarrow{EF}\mathrm{\perp }\overrightarrow{BD}$

Vậy ta chứng minh được EF vuông góc với DB

Bài 3 trang 73 Toán 10 Tập 2: Tìm tọa độ giao điểm và góc giữa hai đường thẳng $d_1$ và $d_2$ trong mỗi trường hợp sau:

a) $d_1:x-y+2=0$ và $d_2:x+y+4=0$

b) $d_1:\{\begin{array}{l}x=1+t\\ y=3+2t\end{array}$ và $d_2:x-3y+2=0$

c)  $d_1:\{\begin{array}{l}x=2-t\\ y=5+3t\end{array}$ và $d_2:\{\begin{array}{l}x=1+3t^{\prime }\\ y=3+t^{\prime }\end{array}$

Phương pháp giải 

+) Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ phương trình tạo bởi hai phương trình đường thẳng

+) Góc giữa hai đường thẳng được tính bằng công thức $\cos \left(d_1,d_2\right)=\frac{\left|a_1{a}_2+b_1{b}_2\right|}{\sqrt{{a_1}^2+{b_1}^2}.\sqrt{{a_2}^2+{b_2}^2}}$ với $\overrightarrow{n_1}=\left(a_1;b_1\right),\overrightarrow{n_2}=\left(a_2;b_2\right)$ lần lượt là vectơ pháp tuyến của đường thẳng $d_1$ và $d_2$

Lời giải 

a) Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

$\{\begin{array}{l}x-y+2=0\\ x+y+4=0\end{array}\iff \{\begin{array}{l}x=-3\\ y=-1\end{array}$

$\cos \left(d_1,d_2\right)=\frac{\left|1.1+(-1).1\right|}{\sqrt{1^2+{\left(-1\right)}^2}.\sqrt{1^2+1^2}}=0\Rightarrow d_1\mathrm{\perp }{d}_2$

Vậy hai đường thẳng $d_1$ và $d_2$ vuông góc với nhau tại điểm có tọa độ $(-3;-1)$

b) Đường thẳng $d_1$ có phương trình tổng quát là: $d_1:2x-y+1=0$

Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

$\{\begin{array}{l}2x-y+1=0\\ x-3y+2=0\end{array}\iff \{\begin{array}{l}x=-\frac{1}{5}\\ y=\frac{3}{5}\end{array}$

$\cos \left(d_1,d_2\right)=\frac{\left|2.\left(-1\right)+1.(-3)\right|}{\sqrt{2^2+{\left(-1\right)}^2}.\sqrt{1^2+{\left(-3\right)}^2}}=\frac{\sqrt{2}}{2}\Rightarrow \left(d_1,d_2\right)={45}^{\circ }$

Vậy hai đường thẳng $d_1$ và $d_2$ cắt nhau tại điểm có tọa độ $\left(-\frac{1}{5};\frac{3}{5}\right)$ và góc giữa chúng là ${45}^{\circ }$

c) Đường thẳng $d_1$ và $d_2$ lần lượt có phương trình tổng quát là:

$d_1:3x+y-11=0,d_2:x-3y+8=0$

Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:

$\{\begin{array}{l}3x+y-11=0\\ x-3y+8=0\end{array}\iff \{\begin{array}{l}x=\frac{5}{2}\\ y=\frac{7}{2}\end{array}$

$\cos \left(d_1,d_2\right)=\frac{\left|3.1+1.(-3)\right|}{\sqrt{3^2+1^2}.\sqrt{1^2+{\left(-3\right)}^2}}=0\Rightarrow \left(d_1,d_2\right)={90}^{\circ }$

Vậy hai đường thẳng $d_1$ và $d_2$ vuông góc tại điểm có tọa độ $\left(\frac{5}{2};\frac{7}{2}\right)$