Với giải Câu hỏi trang 74 Toán 10 Tập 2 Chân trời sáng tạo trong Bài tập cuối chương 9 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Chân trời sáng tạo trang 74 Bài tập cuối chương 9

Bài 4 trang 74 Toán 10 Tập 2: Tính bán kính của đường tròn tâm $M(-2;3)$ và tiếp xúc với đường thẳng $d:14x-5y+60=0$

Phương pháp giải

Đường tròn với tâm $M(x;y)$ và tiếp tuyến d: $ax+by+c=0$ có $R=d\left(M,d\right)=\frac{\left|ax+by+c\right|}{\sqrt{a^2+b^2}}$ 

Lời giải 

Bán kính của đường tròn là:

$R=d\left(M,d\right)=\frac{\left|14.(-2)-5.3+60\right|}{\sqrt{{14}^2+{\left(-5\right)}^2}}=\frac{\sqrt{221}}{13}$

Vậy bán kính cần tìm là $\frac{\sqrt{221}}{13}$

Bài 5 trang 74 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng: $\mathrm{\Delta }:6x+8y-13=0$ và ${\mathrm{\Delta }}^{\prime }:3x+4y-27=0$

Phương pháp giải

Cho $\mathrm{\Delta }//{\mathrm{\Delta }}^{\prime }$, khi đó: $d(\mathrm{\Delta },{\mathrm{\Delta }}^{\prime })=d\left(M,\mathrm{\Delta }\right)=\frac{\left|ax+by+c\right|}{\sqrt{a^2+b^2}}$ với $M(x;y)\in {\mathrm{\Delta }}^{\prime }$ bất kì và $\mathrm{\Delta }:ax+by+c=0$

Lời giải 

Ta có $\frac{6}{3}=\frac{8}{4}\ne \frac{-13}{-27}$ nên hai đường thẳng này song song với nhau.

Chọn điểm $A(9;0)\in {\mathrm{\Delta }}^{\prime }$ ta có:

$d\left(\mathrm{\Delta },{\mathrm{\Delta }}^{\prime }\right)=d\left(A,\mathrm{\Delta }\right)=\frac{\left|6.9+8.0-13\right|}{\sqrt{6^2+8^2}}=\frac{41}{10}$

Vậy khoảng cách giữa hai đường thẳng đã cho là $\frac{41}{10}$

Bài 6 trang 74 Toán 10 Tập 2: Tìm tâm và bán kính của các đường tròn có phương trình:

a) ${\left(x-2\right)}^2+{\left(y-7\right)}^2=64$

b) ${\left(x+3\right)}^2+{\left(y+2\right)}^2=8$

c) $x^2+y^2-4x-6y-12=0$

Phương pháp giải

+) Với phương trình có dạng ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$ thì đường tròn có tâm là $I(a;b)$ và bán kính R

+) Với phương trình có dạng $x^2+y^2-2ax-2by+c=0$ thì đường tròn có tâm là $I(a;b)$ và bán kính $R=\sqrt{a^2+b^2-c}$

Lời giải 

a) Phương trình đường tròn ${\left(x-2\right)}^2+{\left(y-7\right)}^2=64$ có dạng ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$ nên đường tròn có tâm là $I(2;7)$ và bán kinh $R=\sqrt{64}=8$

b) Phương trình đường tròn ${\left(x+3\right)}^2+{\left(y+2\right)}^2=8$ có dạng ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$ nên đường tròn có tâm là $I(-3;-2)$ và bán kinh $R=\sqrt{8}=2\sqrt{2}$

c) Phương trình đường tròn $x^2+y^2-4x-6y-12=0$ có dạng $x^2+y^2-2ax-2by+c=0$ nên đường tròn có tâm là $I(2;3)$ và bán kinh $R=\sqrt{2^2+3^2+12}=5$

Bài 7 trang 74 Toán 10 Tập 2: Lập phương trình đường tròn trong các trường hợp sau:

a) Có tâm $I(-2;4)$ và bán kính bằng 9

b) Có tâm $I(1;2)$ và đi qua điểm $A(4;5)$

c) Đi qua hai điểm $A(4;1),B(6;5)$ và có tâm nằm trên đường thẳng $4x+y-16=0$

d) Đi qua gốc tọa độ và cắt 2 trục tọa độ tại các điểm có hoành độ a và tung độ là b

Phương pháp giải

a) Với tâm là $I(a;b)$ và bán kính R, phương trình đường tròn có dạng ${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$

b)       Bước 1: Xác định bán kính (khoảng cách IA)

          Bước 2: Viết phương trình như câu a)

c)       Bước 1: Từ phương trình mà tâm nằm trên đó, gọi tọa độ tâm qua một ẩn

          Bước 2; Giải phương trình IA=IB tìm tọa độ điểm I (với I là tâm đường tròn)

          Bước 3: Viết phương trình đường tròn như câu a)

d)       Bước 1: Giả sử phương trình đường tròn có dạng $x^2+y^2-2mx-2ny+p=0$ (với tâm $I(m;n),R=\sqrt{m^2+n^2-p}$

          Bước 2: Thay tọa độ các điểm theo giả thiết vào phương trình, xác định m, n, p)

          Bước 3: Xác định phương trình đường tròn

Lời giải 

a) Ta có phương trình đường tròn là $(C_1):{\left(x+2\right)}^2+{\left(y-4\right)}^2=81$

b) Ta có: $\overrightarrow{IA}=(3;3)\Rightarrow IA=3\sqrt{2}=R$

Suy ra phương trình đường tròn là; $C_2:{\left(x-1\right)}^2+{\left(y-2\right)}^2=18$

c) Vì tâm đường tròn nằm trên đường thẳng $4x+y-16=0$ nên có tọa độ $I\left(a;16-4a\right)$

Ta có: $IA=\sqrt{{\left(a-4\right)}^2+{\left(16-4a-1\right)}^2},IB=\sqrt{{\left(a-6\right)}^2+{\left(16-4a-5\right)}^2}$

A, B thuộc đường tròn nên $IA=IB\Rightarrow \sqrt{{\left(a-4\right)}^2+{\left(16-4a-1\right)}^2}=\sqrt{{\left(a-6\right)}^2+{\left(16-4a-5\right)}^2}$

$\begin{array}{l}\Rightarrow {\left(a-4\right)}^2+{\left(16-4a-1\right)}^2={\left(a-6\right)}^2+{\left(16-4a-5\right)}^2\\ \Rightarrow {\left(a-4\right)}^2+{\left(15-4a\right)}^2={\left(a-6\right)}^2+{\left(11-4a\right)}^2\\ \Rightarrow -28a=-84\Rightarrow a=3\end{array}$

Suy ra tâm đường tròn là $I(3;4)$, bán kính $R=IA=\sqrt{10}$

Phương trình đường tròn trên là $(C_3):{\left(x-3\right)}^2+{\left(y-4\right)}^2=10$

d) Giả sử phương trình đường tròn có dạng $x^2+y^2-2mx-2ny+p=0$ (với tâm $I(m;n),R=\sqrt{m^2+n^2-p}$)

Đường tròn đi qua gốc tọa độ và cắt 2 trục tọa độ tại các điểm có hoành độ a và tung độ là b nên ta có hệ phương trình:

Ta có điều kiện $a,b\ne 0$, vì khi bằng 0 thì trùng với gốc tọa độ

$\{\begin{array}{l}{0}^2+0^2-2m.0-2n.0+p=0\\ a^2+0^2-2ma-2n.0+p=0\\ 0^2+b^2-2m.0-2nb+p=0\end{array}\iff \{\begin{array}{l}p=0\\ a^2-2ma=0\\ b^2-2nb=0\end{array}\iff \{\begin{array}{l}p=0\\ m=\frac{a}{2}\\ n=\frac{b}{2}\end{array}$

Vậy phương trình chính tắc của đường tròn trên là $x^2+y^2-ax-by=0$

Bài 8 trang 74 Toán 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn $(C):{\left(x-5\right)}^2+{\left(y-3\right)}^2=100$ tại điểm $M(11;11)$

Phương pháp giải 

Bước 1: Xác định vectơ pháp tuyến của đường thẳng (là vectơ $\overrightarrow{IM}$ với I là tâm đường tròn)

Bước 2: Viết phương trình đường thẳng đó $a\left(x-x_0\right)+b\left(y-y_0\right)=0$ với $\overrightarrow{n}=(a;b)$ là vectơ pháp tuyến và $M\left(x_0;y_0\right)$ thuộc đường thẳng

Lời giải 

Ta có tâm của đường tròn $I(5;3)$

Tiếp tuyến nhận vectơ $\overrightarrow{IM}$ làm vectơ pháp tuyến nên ta có: $\overrightarrow{n}=\overrightarrow{IM}=\left(6;8\right)$

Điểm M nằm trên tiếp tuyến nên ta có phương trình:

$6\left(x-11\right)+8\left(y-11\right)=0\iff 3x+4y-77=0$

Vậy phương trình tiếp tuyến của đường tròn $(C):{\left(x-5\right)}^2+{\left(y-3\right)}^2=100$ tại điểm $M(11;11)$ là $3x+4y-77=0$

Bài 9 trang 74 Toán 10 Tập 2: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

a) $\frac{x^2}{100}+\frac{y^2}{16}=1$

b) $\frac{x^2}{25}+\frac{y^2}{16}=1$

c) $x^2+16y^2=16$

Phương pháp giải

Bước 1: Đưa phương trình về dạng phương trình chính tắc của elip

Bước 2: Phương trình có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, $c=\sqrt{a^2-b^2}$ta có:

         Tọa độ các tiêu điểm: $F_1\left(-c;0\right),F_2\left(c;0\right)$

          Tọa độ các đỉnh: $A(0;b),B(a;0),C(0;-b),D(-a;0)$

          Độ dài trục lớn 2a

          Độ dài trục nhỏ 2b

Lời giải 

a) Phương trình $\frac{x^2}{100}+\frac{y^2}{16}=1$ đã có dạng phương trình chính tắc $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ nên ta có: $a=10,b=4\Rightarrow c=\sqrt{a^2-b^2}=\sqrt{{10}^2-4^2}=2\sqrt{21}$

Suy ra ta có:

Tọa độ các tiêu điểm: $F_1\left(-2\sqrt{21};0\right),F_2\left(2\sqrt{21};0\right)$

Tọa độ các đỉnh: $A(0;4),B(10;0),C(0;-4),D(-10;0)$

Độ dài trục lớn 20

Độ dài trục nhỏ 8

b) Phương trình $\frac{x^2}{25}+\frac{y^2}{16}=1$ đã có dạng phương trình chính tắc $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ nên ta có: $a=5,b=4\Rightarrow c=\sqrt{a^2-b^2}=\sqrt{5^2-4^2}=3$

Suy ra ta có:

Tọa độ các tiêu điểm: $F_1\left(-3;0\right),F_2\left(3;0\right)$

Tọa độ các đỉnh: $A(0;4),B(5;0),C(0;-4),D(-5;0)$

Độ dài trục lớn 10

Độ dài trục nhỏ 8

c) $x^2+16y^2=16\iff \frac{x^2}{16}+\frac{y^2}{1}=1$

Vậy ta có phương trình chính tắc của elip đã cho là $\frac{x^2}{16}+\frac{y^2}{1}=1$

Suy ra $a=4,b=1\Rightarrow c=\sqrt{a^2-b^2}=\sqrt{4^2-1^2}=\sqrt{15}$

Từ đó ta có:

Tọa độ các tiêu điểm: $F_1\left(-\sqrt{15};0\right),F_2\left(\sqrt{15};0\right)$

Tọa độ các đỉnh: $A(0;1),B(4;0),C(0;-1),D(-4;0)$

Độ dài trục lớn 8

Độ dài trục nhỏ 2

Bài 10 trang 74 Toán 10 Tập 2: Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:

a) Đỉnh $(5;0),(0;4)$

b) Đỉnh $(5;0)$, tiêu điểm $(3;0)$

c) Độ dài trục lớn 16, độ dài trục nhỏ 12

d) Độ dài trục lớn 20, tiêu cự 12

Phương pháp giải

Bước 1: Xác định a, b, c

Bước 2: Viết phương trình chính tắc của elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, $c=\sqrt{a^2-b^2}$

Lời giải

a) Từ giả thiết ta có $a=5,b=4$

Suy ra phương trình chính tắc của elip là: $\frac{x^2}{25}+\frac{y^2}{16}=1$

b) Ta có: $a=5,c=3\Rightarrow b=\sqrt{a^2-c^2}=\sqrt{5^2-3^2}=4$

Suy ra phương trình chính tắc của elip là: $\frac{x^2}{25}+\frac{y^2}{16}=1$

c) Từ giả thiết ta có: $2a=16,2b=12\Rightarrow a=8,b=6$

Suy ra phương trình chính tắc của elip là: $\frac{x^2}{64}+\frac{y^2}{36}=1$

d) Từ giả thiết ta có: $2a=20,2c=12\Rightarrow a=10,c=6\Rightarrow b=\sqrt{a^2-c^2}=\sqrt{{10}^2-6^2}=8$

Suy ra phương trình chính tắc của elip là: $\frac{x^2}{100}+\frac{y^2}{64}=1$

Bài 11 trang 74 Toán 10 Tập 2: Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:

a) $\frac{x^2}{16}-\frac{y^2}{9}=1$

b)  $\frac{x^2}{64}-\frac{y^2}{36}=1$

c) $x^2-16y^2=16$

d) $9x^2-16y^2=144$

Phương pháp giải

Bước 1: Đưa phương trình về dạng phương trình chính tắc của hypebol

Bước 2: Phương trình có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$, $c=\sqrt{a^2+b^2}$ta có:

          Tọa độ các tiêu điểm: $F_1\left(-c;0\right),F_2\left(c;0\right)$

          Tọa độ các đỉnh: $A(0;b),B(a;0),C(0;-b),D(-a;0)$

          Độ dài trục thực 2a

          Độ dài trục ảo 2b

Lời giải 

a) Phương trình $\frac{x^2}{16}-\frac{y^2}{9}=1$ đã có dạng phương trình chính tắc $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên ta có: $a=4,b=3\Rightarrow c=\sqrt{a^2+b^2}=\sqrt{4^2+3^2}=5$

Suy ra ta có:

Tọa độ các tiêu điểm: $F_1\left(-5;0\right),F_2\left(5;0\right)$

Tọa độ các đỉnh: $A(0;3),B(4;0),C(0;-3),D(-4;0)$

Độ dài trục thực 8

Độ dài trục ảo 6

b) Phương trình $\frac{x^2}{64}-\frac{y^2}{36}=1$ đã có dạng phương trình chính tắc $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ nên ta có: $a=8,b=6\Rightarrow c=\sqrt{a^2+b^2}=\sqrt{8^2+6^2}=10$

Suy ra ta có:

Tọa độ các tiêu điểm: $F_1\left(-10;0\right),F_2\left(10;0\right)$

Tọa độ các đỉnh: $A(0;6),B(8;0),C(0;-6),D(-8;0)$

Độ dài trục thực 16

Độ dài trục ảo 12

c) $x^2-16y^2=16\iff \frac{x^2}{16}-\frac{y^2}{1}=1$

Vậy ta có phương trình chính tắc của hypebol đã cho là $\frac{x^2}{16}-\frac{y^2}{1}=1$

Suy ra $a=4,b=1\Rightarrow c=\sqrt{a^2+b^2}=\sqrt{4^2+1^2}=\sqrt{17}$

Từ đó ta có:

Tọa độ các tiêu điểm: $F_1\left(-\sqrt{17};0\right),F_2\left(\sqrt{17};0\right)$

Tọa độ các đỉnh: $A(0;1),B(4;0),C(0;-1),D(-4;0)$

Độ dài trục thực 8

Độ dài trục ảo 2

d) $9x^2-16y^2=144\iff \frac{x^2}{\frac{144}{9}}-\frac{y^2}{\frac{144}{16}}=1$

Vậy ta có phương trình chính tắc của hypebol đã cho là $\frac{x^2}{16}-\frac{y^2}{9}=1$

Suy ra $a=4,b=3\Rightarrow c=\sqrt{a^2+b^2}=\sqrt{4^2+3^2}=5$

Từ đó ta có:

Tọa độ các tiêu điểm: $F_1\left(-5;0\right),F_2\left(5;0\right)$

Tọa độ các đỉnh: $A(0;3),B(4;0),C(0;-3),D(-4;0)$

Độ dài trục thực 8

Độ dài trục ảo 6

Bài 12 trang 74 Toán 10 Tập 2: Viết phương trình chính tắc của hypebol thỏa mãn từng điều kiện sau:

a) Đỉnh $(3;0)$, tiêu điểm $(5;0)$

b) Độ dài trục thực 8, độ dài trục ảo 6

Phương pháp giải

Bước 1: Xác định a, b, c

Bước 2: Viết phương trình chính tắc của hypebol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với $b=\sqrt{c^2-a^2}$

Lời giải 

a) Từ giả thiết ta có: $a=3,c=5\Rightarrow b=\sqrt{c^2-a^2}=\sqrt{5^2-3^2}=4$

Ta có phương trình chính tắc của hypebol là: $\frac{x^2}{9}-\frac{y^2}{16}=1$

b) Ta có: $2a=8,2b=6\Rightarrow a=4,b=3$

Suy ra phương trình chính tắc của hypebol là $\frac{x^2}{16}-\frac{y^2}{9}=1$

Bài 13 trang 74 Toán 10 Tập 2: Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a) $y^2=12x$

b) $y^2=x$

Phương pháp giải

Bước 1: Xác định tiêu cự của parabol (với phương trình chính tắc $y^2=2px$)

Bước 2: Xác định tọa độ tiêu điểm $F\left(\frac{p}{2};0\right)$

Bước 3: Viết phương trình đường chuẩn có dạng $\mathrm{\Delta }:x+\frac{p}{2}=0$

Lời giải

a) Từ phương trình chính tắc $y^2=12x$ ta có $p=6$

Suy ra

+) Tiêu điểm của parabol $F(3;0)$

+) Phương trình đường chuẩn của parabol $\mathrm{\Delta }:x+3=0$

b) Từ phương trình chính tắc $y^2=x$ ta có $p=\frac{1}{2}$

Suy ra

+) Tiêu điểm của parabol $F(\frac{1}{4};0)$

+) Phương trình đường chuẩn của parabol $\mathrm{\Delta }:x+\frac{1}{4}=0$

Bài 14 trang 74 Toán 10 Tập 2: Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:

a) Tiêu điểm $(4;0)$

b) Đường chuẩn có phương trình $x=-\frac{1}{6}$

c) Đi qua điểm $(1;4)$

d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8

Phương pháp giải

a,b)    Bước 1: Xác định p

                   +) Tiêu điểm có tọa độ $F\left(\frac{p}{2};0\right)$

                   +) Đường chuẩn có phương trình $\mathrm{\Delta }:x+\frac{p}{2}=0$

          Bước 2: Viết phương trình chính tắc của parabol có dạng $y^2=2px$

c)       Bước 1: Gọi phương trình chính tắc của parabol có dạng $y^2=2px$

          Bước 2: Thay tọa độ điểm trên tìm p

          Bước 3: Xác định phương trình chính tắc

d)       Bước 1: Gọi tiêu điểm và phương trình đường chuẩn tổng quát

          Bước 2: Từ khoảng cách tìm p

          Bước 3: Xác định phương trình chính tắc $y^2=2px$

Lời giải 

a) Tiêu điểm có tọa độ $(4;0)$ nên ta có $p=8$

Suy ra phương trình chính tắc của parabol là: $y^2=16x$

b) Đường chuẩn có phương trình $x=-\frac{1}{6}$, nên ta có $p=-\frac{1}{3}$

Suy ra phương trình chính tắc của parabol có dạng $y^2=-\frac{2}{3}x$

c) Gọi phương trình chính tắc của parabol có dạng $y^2=2px$

Thay tọa độ điểm $(1;4)$ vào phương trình $y^2=2px$ ta có:

$4^2=2p.1\Rightarrow p=8$

Vậy phương trình chính tắc của parabol là $y^2=16x$

d) Gọi $F\left(\frac{p}{2};0\right)$, $\mathrm{\Delta }:x+\frac{p}{2}=0$ lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:

$d\left(F,\mathrm{\Delta }\right)=\frac{\left|\frac{p}{2}+\frac{p}{2}\right|}{1}=8\Rightarrow p=8$

Vậy phương trình chính tắc của parabol là $y^2=16x$

Bài 15 trang 74 Toán 10 Tập 2: Một gương lõm có mặt cắt hình parabol như hình 1, có tiêu điểm cách đỉnh 5 cm. Cho biết bề sâu của gương là 45 cm. Tính khoảng cách AB

Phương pháp giải

Bước 1: Từ tiêu điểm $F(\frac{p}{2};0)$ viết phương trình chính tắc của parabol có dạng

Bước 2: Thay $x=45$ vào phương trình trên tìm $y_A$

Bước 3: Xác định khoảng cách $AB=2.y_A$$y^2=2px$

Lời giải 

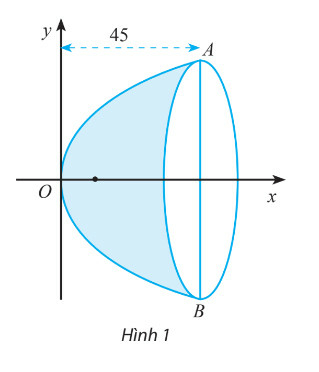
Từ giả thiết ta có tiêu điểm $F(5;0)$, suy ra $\frac{p}{2}=5$ hay $p=10$.

Vậy phương trình chính tắc của parabol là: $y^2=20x$

Chiều sâu của gương là 45 cm tương ứng với $x_A=45$, thay $x_A=45$ vào phương trình $y^2=20x$ ta có: $y^2=20.45=900\Rightarrow y_A=30\Rightarrow AB=2y_A=60$

Vậy khoảng cách AB là $60cm$