Với giải Câu hỏi trang 75 Toán 10 Tập 2 Chân trời sáng tạo trong Bài tập cuối chương 9 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 75 Bài tập cuối chương 9
a) Viết phương trình chính tắc của parabol
b) Tính khoảng cách từ tâm đường ống đến đỉnh của parabol
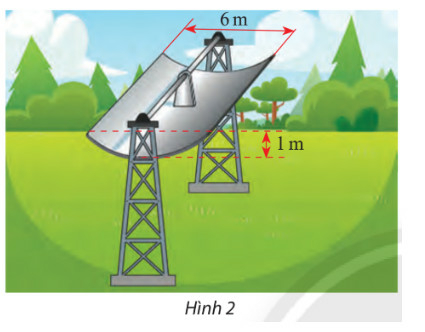
Phương pháp giải
a) Bước 1: Xác định điểm nằm trên đường parabol
Bước 2: Giả sử phương trình của parabol là , thay tọa độ điểm vừa tìm được tìm p
Bước 3: Xác định phương trình chính tắc của parabol
b) Xác định tọa độ của tiêu điểm
Lời giải
a) Vẽ lại parabol mô phỏng mặt cắt trên như hình dưới
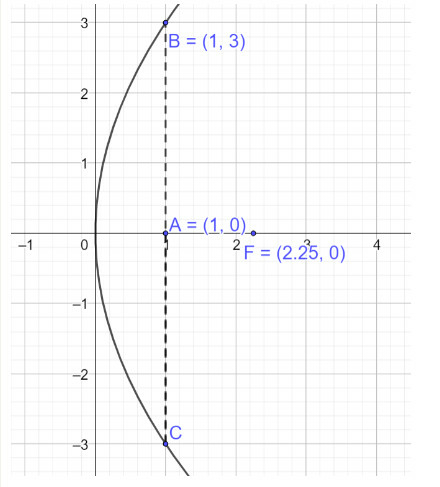
Ta có:
Giả sử phương trình chính tắc của parabol có dạng
Thay tọa độ điểm B vào phương trình ta có:
Vậy phương trình chính tắc của parabol mô phỏng mặt cắt trên là
b) Khoảng cách từ tâm đường ống đến đỉnh của parabol chính là độ dài từ đỉnh tới tiêu điểm của parabol
Từ phương trình chính tắc ta có tiêu điểm
Vậy khoảng cách từ tâm đường ống đến đỉnh của parabol là m
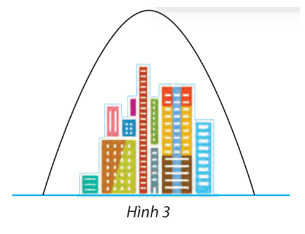
Phương pháp giải
Bước 1: Gắn hệ trục tọa độ Oxy
Bước 2: Gọi phương trình chính tắc mô phỏng cổng là
Bước 3: Thay điểm M vào phương trình, xác định phương trình parabol
Bước 4: Xác định chiều cao của cổng
Lời giải
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
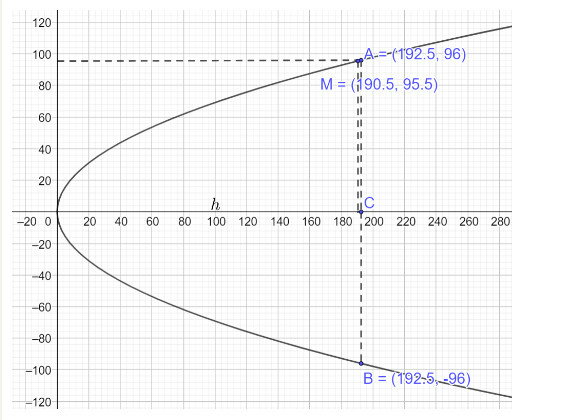
Phương trình parabol mô phỏng cổng có dạng
Theo giả thiết
Thay tọa độ các điểm vào phương trình ta có:
Vậy chiều cao của cổng gần bằng 192,5 m
a) Giả sử tâm ván gỗ trùng với đỉnh của parabol, tìm phương trình chính tắc của parabol
b) Điểm có độ võng 1 cm cách tâm ván gỗ bao xa?
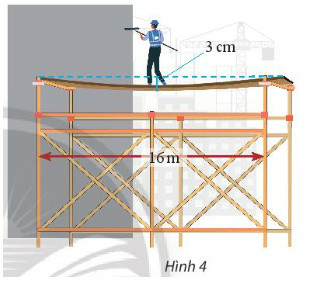
Phương pháp giải
a) Bước 1: Giả sử phương trình chính tắc của parabol có dạng
Bước 2: Từ giả thiết, xác định điểm thuộc parabol
Bước 3: Thay tọa độ điểm đó vào phương trình , tìm p và xác định phương trình chính tắc của parabol
b) Thay vào phương trình chính tắc vừa tìm được tìm y
Lời giải
a) Ta vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
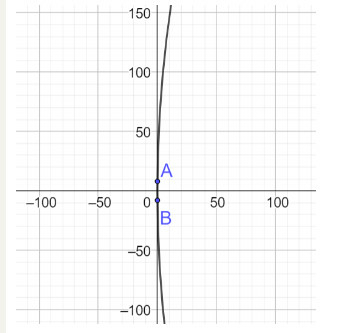
Giả sử phương trình chính tắc của parabol có dạng
Từ giả thiết ta có:
Thay tọa độ điểm A vào phương trình ta được
Vậy Phương trình chính tắc của parabol có dạng
b) Thay vào phương trình ta có
Vậy điểm có độ võng 1 cm cách tâm ván gỗ gần bằng 46,2 m
Chú ý khi giải: đổi về cùng đơn vị đo
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 73 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho bốn điểm...
Bài 4 trang 74 Toán 10 Tập 2: Tính bán kính của đường tròn tâm và tiếp xúc với đường thẳng ...
Bài 5 trang 74 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng: và ....
Bài 6 trang 74 Toán 10 Tập 2: Tìm tâm và bán kính của các đường tròn có phương trình...
Bài 7 trang 74 Toán 10 Tập 2: Lập phương trình đường tròn trong các trường hợp sau...
Bài 8 trang 74 Toán 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn tại điểm ...
Bài 10 trang 74 Toán 10 Tập 2: Viết phương trình chính tắc của elip thỏa mãn từng điều kiện...
Bài 13 trang 74 Toán 10 Tập 2: Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.