Với giải Câu hỏi trang 28 Toán 10 Tập 2 Kết nối tri thức trong Bài tập cuối chương 6 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 28: Bài tập cuối chương 6
Bài 6.24 trang 28 SGK Toán 10 Tập 2: Tìm tập xác định của hàm số là:
A.
B.
C.
D.
Phương pháp giải:
- Giải bất phương trình
- Kết luận tập xác định của hàm số.
Lời giải:
Để hàm số xác định
Vậy tập xác định của hàm số là:
Chọn B.
Bài 6.25 trang 28 SGK Toán 10 Tập 2: Parabol có đỉnh là:
A.
B.
C.
D.
Phương pháp giải:
- Xác định các hệ số
- Tính
- Xác định tọa độ đỉnh
Lời giải:
Parabol có
Ta có:
Tọa độ đỉnh là:
Chọn D.
Bài 6.26 trang 28 SGK Toán 10 Tập 2: Hàm số
A. Đồng biến trên khoảng
B. Đồng biến trên khoảng
C. Nghịch biến trên khoảng
D. Nghịch biến trên khoảng
Phương pháp giải:
- Xác định trục đối xứng của hàm số
- Xác định khoảng đồng biến, nghịch biến của hàm số
Lời giải:
Trục đối xứng của hàm số là:
Vì nân hàm số đồng biến trên khoảng và nghịch biến trên khoảng
Chọn C.
Bài 6.27 trang 28 SGK Toán 10 Tập 2: Bất phương trình nghiệm đúng với mọi khi
A.
B.
C.
D.
Phương pháp giải:
- Tính
- Giải bất phương trình để bất phương trình có nghiệm đúng với mọi
Lời giải:
Để nghiệm đúng với mọi
Ta có có hai nghiệm phân biệt và
Mặt khác: nên ta có bảng xét dấu sau:

Vậy tập nghiệm của bất phương trình là:
Chọn A.
Bài 6.28 trang 28 SGK Toán 10 Tập 2: Tập nghiệm của phương trình là:
A.
B.
C.
D.
Phương pháp giải:
- Tìm điều kiện để phương trình có nghĩa
- Bình phương hai vế của phương trình để mất dấu căn
- Đưa về dạng phương trình và giải:
Lời giải:
ĐK:
TXĐ của phương trình là:
Giải phương trình:
Ta thấy thỏa mãn.
Vậy tập nghiệm của phương trình là:
Chọn C.
B. Tự luận
Bài 6.29 trang 28 SGK Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:
a)
b)
Phương pháp giải:
- Giải bất phương trình và
- Kết luận tập xác định của hàm số
Lời giải:
a) Tập xác đinh của hàm số là:
Vậy tập xác định của hàm số là:
b) Tập xác định của hàm số là:
Vậy tập xác định của hàm số là:
a)
b)
c)
d)
Phương pháp giải:
Cho hàm số
- Xác định tọa độ đỉnh
- Trục đối xứng
- Giao với trục
- Xác định tập giá trị của hàm số
- Từ đồ thị tìm khoảng đồng biến, nghịch biến của hàm số
Lời giải:
a)
Ta có: nên parabol quay bề lõm xuống dưới.
Đỉnh Trục đối xứng Giao điểm của đồ thị với trục là: Parabol cắt trục hoành tại
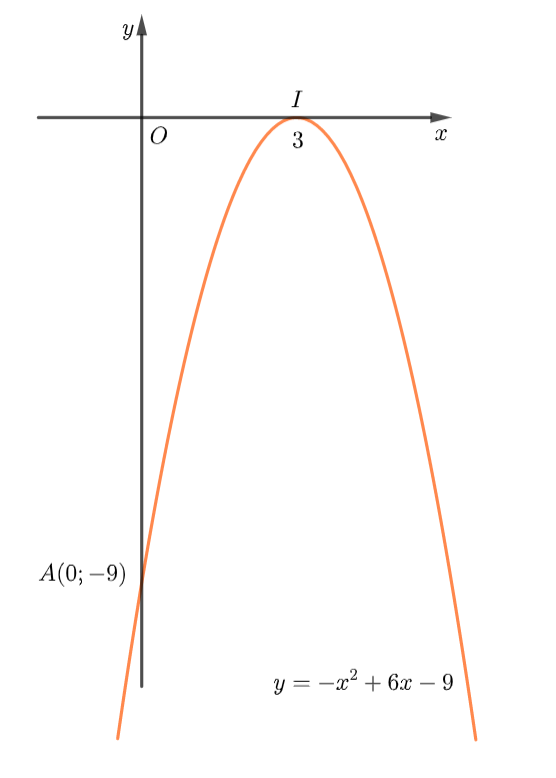
Tập giá trị của hàm số là:
Từ đồ thị ta thấy: Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
b)
Ta có: nên parabol quay bề lõm xuống dưới.
Đỉnh Trục đối xứng Giao điểm của hàm số với trục là: Giao điểm của hàm số với trục là: và
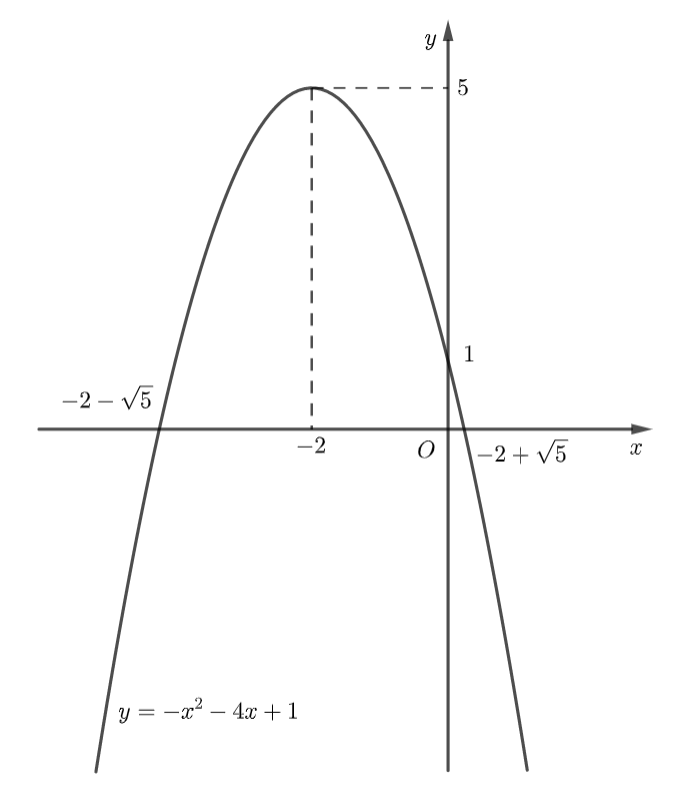
Tập giá trị của hàm số là:
Từ đồ thị ta thấy: Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
c)
Ta có: nên parabol quay bề lõm lên trên.
Đỉnh Trục đối xứng Giao điểm của hàm số với trục là: Giao điểm của hàm số với trục là: và
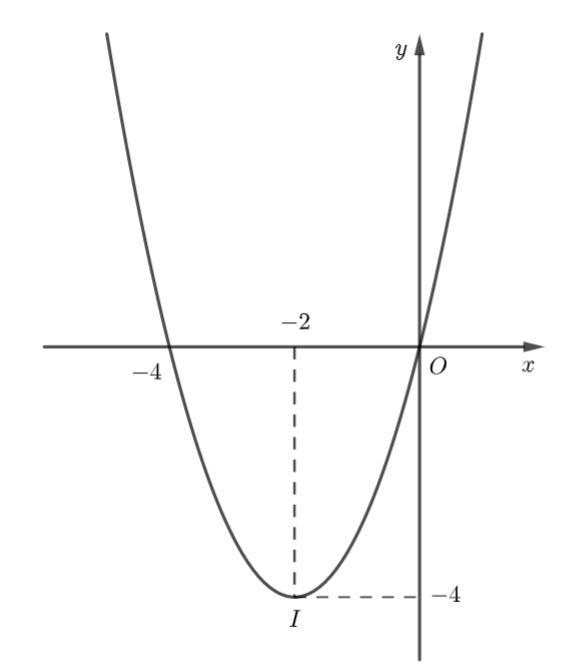
Tập giá trị của hàm số là:
Từ đồ thị ta thấy: Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
d)
Ta có: nên parabol quay bề lõm lên trên.
Đỉnh Trục đối xứng giao điểm của hàm số với trục là: Đồ thị hàm số không có giao điểm với trục Lấy điểm thuộc đồ thị hàm số, điểm đối xứng với điểm đó qua trục đối xứng là:
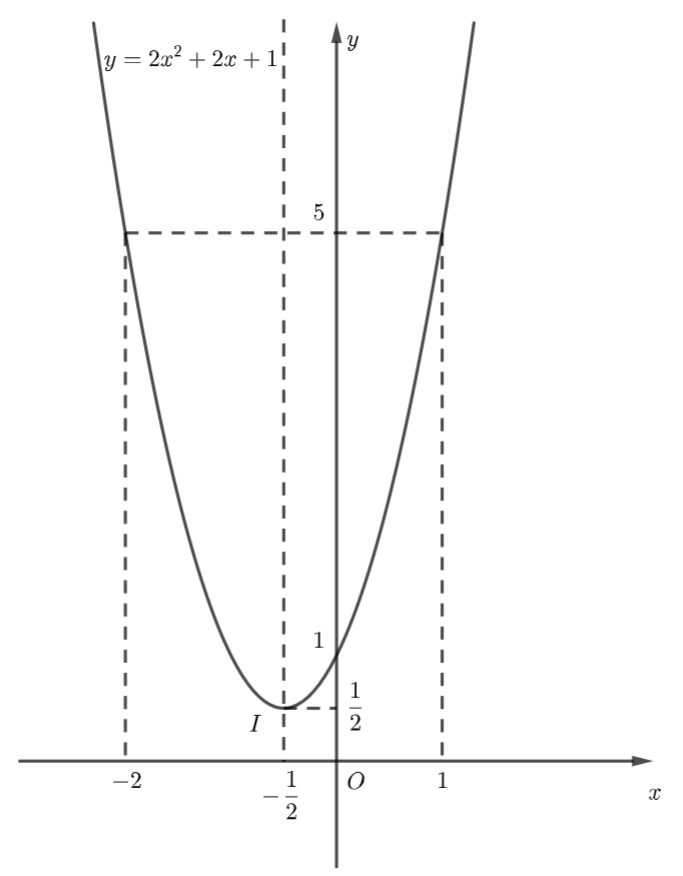
Tập giá trị của hàm số là:
Từ đồ thị ta thấy: Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
Bài 6.31 trang 28 SGK Toán 10 Tập 2: Xác định parabol trong mỗi trường hợp sau:
a) đi qua hai điểm và .
b) đi qua điểm và nhận đường thẳng làm trục đối xứng.
c) có đỉnh là
Phương pháp giải:
a) thay các điểm và vào parabol để giải hệ phương trình tìm .
b) thay điểm vào parabol và trục đối xứng để giải hệ phương trình tìm .
c) thay đỉnh vào parabol và trục đối xứng để giải hệ phương trình tìm .
Lời giải:
a) Theo giả thiết, hai điểm và thuộc parabol nên ta có:
Vậy hàm số cần tìm là:
b) Parabol nhận làm trục đối xứng nên
Điểm thuộc parabol nên
Do đó, ta có hệ phương trình:
Vậy hàm số cần tìm là:
c) Parabol có đỉnh nên ta có:
Vậy hàm số cần tìm là:
Bài 6.32 trang 28 SGK Toán 10 Tập 2: Giải các bất phương trình sau:
a)
b)
c)
d)
Phương pháp giải:
- Tìm nghiệm của các phương trình trên
- Lập bảng xét dấu
- Kết luận tập nghiệm của bất phương trình
Lời giải:
a)
Tam thức có nên hai nghiệm phân biệt và
Mặt khác do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là:
b)
Tam thức có nên phương trình có hai nghiệm phân biệt và
Mặt khác do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là:
c)
Tam thức
nên luôn âm với mọi
bất phương trình vô nghiệm
d)
Tam thức có hệ số nên luôn dướng với mọi tức là với mọi
bất phương trình vô nghiệm
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 6.24 trang 28 SGK Toán 10 Tập 2: Tìm tập xác định của hàm số là...
Bài 6.25 trang 28 SGK Toán 10 Tập 2: Parabol có đỉnh là:...
Bài 6.26 trang 28 SGK Toán 10 Tập 2: Hàm số ...
Bài 6.27 trang 28 SGK Toán 10 Tập 2: Bất phương trình nghiệm đúng với mọi khi...
Bài 6.28 trang 28 SGK Toán 10 Tập 2: Tập nghiệm của phương trình là:...
Bài 6.29 trang 28 SGK Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:...
Bài 6.31 trang 28 SGK Toán 10 Tập 2: Xác định parabol trong mỗi trường hợp sau:...
Bài 6.32 trang 28 SGK Toán 10 Tập 2: Giải các bất phương trình sau:...
Bài 6.33 trang 29 SGK Toán 10 Tập 2: Giải các phương trình sau:...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.