Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 4: Liên hệ giữa phép chia và phép khai phương
Trả lời câu hỏi giữa bài:
Lời giải:
Ta có:
+)
+)
Sử dụng công thức khai phương 1 thương:
Với ta có
Lời giải:
a)
b)
Sử dụng công thức:
Với ta có
Lời giải:
a)
b)
Lời giải:
a) Ta có
b) Ta có
Bài tập trang 18-20 SGK Toán 9
a) ; b) ;
c) ; d) .
+) Sử dụng định lí: Với số không âm và số dương, ta có:
.
+) Cách đổi hỗn số dương ra phân số:
, với .
Lời giải:
a) Ta có:
.
b) Ta có:
.
c) Ta có:
.
d) Ta có:
.
Phương pháp giải:
Sử dụng các công thức sau:
, với .
, với .
Lời giải:
b)
.
c)
.
d)
.
Bài 30 trang 19 sgk Toán 9 - tập 1: Rút gọn các biểu thức sau
a) với ;
Phương pháp giải:
+) , với .
+) .
+) , nếu .
, nếu .
+) , với .
Lời giải:
a)
Vì nên .
Vì nên .
.
Vậy .
b)
Vì .
Vì nên
.
Vậy .
c)
Vì nên
Vì .
Vậy .
d)
.
Vì nên và
và .
+) , với .
+) Sử dụng kết quả bài 26 trang 16 SGK toán 9 tập 1: Với hai số dương ta có:
Lời giải:
a) +) .
Vì .
b) Bài ra cho nên và đều xác định và dương.
Ta sẽ so sánh với
Theo kết quả bài 26 trang 16 SGK toán 9 tập 1, với hai số dương và ta sẽ có:
Suy ra:
Vậy với
Cách khác 1:
Với ta có
Xét , bình phương hai vế ta được
luôn đúng vì
Vậy với
Cách khác 2:
Bài ra cho nên và đều xác định và dương.
Ta sẽ so sánh với
Ta có là số dương và
Rõ ràng nên (1)
Ta có là số không âm và (2)
Từ (1) và (2) suy ra
(3)
Từ (3) theo định lí so sánh các căn bậc hai số học, ta suy ra
Hay
Hay
Từ kết quả , ta có null
c)
Phương pháp giải:
a,b) + Sử dụng công thức đổi hỗn số ra phân số: .
+ , với .
+ với .
+ , với .
c,d) + , với .
+ với .
+ , với .
+
Lời giải:
a) Ta có:
b) Ta có:
.
c) Ta có:
.
d) Ta có:
.
Bài 33 trang 19 sgk Toán 9 - tập 1
Giải phương trình
a)
Phương pháp giải:
Sử dụng các công thức
+
+ (với )
+
Lời giải:
a)
.
b)
.
Vậy .
c)
.
Vậy .
d)
.
Vậy .
Bài 34 trang 19 sgk Toán 9 - tập 1:Rút gọn các biểu thức sau:
a) với
b) với
c) với và
d) với
Phương pháp giải:
Sử dụng các công thức:
+ với
+
Lời giải:
a) Ta có:
.
(Vì nên và nên .
b) Ta có:
.
( Vì nên
b) Ta có:
Vì
Vì
Do đó: .
Vậy .
d) Ta có:
.
(Vì nên và
Bài 35 trang 20 sgk Toán 9 - tập 1:Tìm , biết:
a) ; b)
Phương pháp giải:
Sử dụng hằng đẳng thức đưa phương trình về dạng
Lời giải:
Ta có:
Vậy phương trình đã cho có hai nghiệm: và .
b) Ta có:
Vậy phương trình có nghiệm và .
Bài 36 trang 20 sgk Toán 9 - tập 1:Mỗi khẳng định sau đúng hay sai ? Vì sao ?
a) ;
b) ;
c) và ;
d) .
+ xác định (hay có nghĩa) khi .
+) Sử dụng định lí so sánh hai căn bậc hai:
, với .
+ , với .
Lời giải:
a) Đúng. Vì
Vì .
b) Sai.
Vì vế phải không có nghĩa do số âm không có căn bậc hai.
c) Đúng.
Vì:
Hay và .
d) Đúng.
Xét bất phương trình đề cho:
Ta có:
Chia cả hai vế của bất đẳng thức cho số dương , ta được:
Vậy phép biến đổi tương đương trong câu d là đúng.
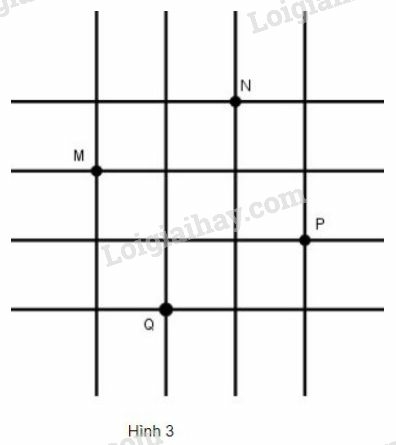
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác .
+ Sử dụng định lí Py-ta-go trong tam giác vuông.
+ Công thức tính diện tích hình vuông cạnh là: .
+ Dấu hiệu nhận biết hình vuông: hình thoi có hai đường chéo bằng nhau (hay tứ giác có bốn cạnh bằng nhau và có hai đường chéo bằng nhau) thì là hình vuông.
Lời giải:
Nối các điểm ta có tứ giác
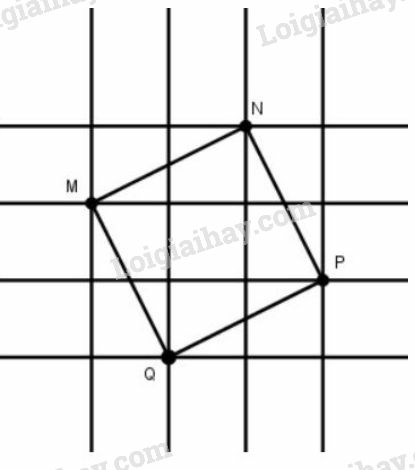
Tứ giác có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài , chiều rộng . Do đó theo định lí Py-ta-go, ta có:
.
Hay là hình thoi.
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài , chiều rộng nên theo định lý Py-ta-go ta có độ dài đường chéo là:
Như vậy hình thoi có hai đường chéo bằng nhau nên là hình vuông.
Vậy diện tích hình vuông bằng .
Lý thuyết Bài 4: Liên hệ giữa phép chia và phép khai phương
Với số không âm và số dương ta có: .
2. Quy tắc khai phương một thương
Muốn khai phương một thương , trong đó a không âm, b dương, ta có thể khai phương lần lượt a và b rồi lấy kết quả thứ nhất chia cho kết quả thứ 2.
3. Quy tắc chia các căn bậc hai
Muốn chia các căn bậc hai của số a không âm cho căn bậc hai của số b dương ta có thể chia a cho cho b rồi khai phương kết quả đó.
Chú ý: Một cách tổng quát, với biểu thức không âm và biểu thức dương ta có
4. Các dạng toán cơ bản
Dạng 1: Tính giá trị biểu thức
Sử dụng: Với biểu thức không âm và biểu thức dương ta có
Ví dụ:
Dạng 2: Rút gọn biểu thức
Sử dụng: Với biểu thức không âm và biểu thức dương ta có
Ví dụ: Rút gọn với
Ta có: 
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.