Toán 8 (Kết nối tri thức) Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Ngọc Nguyễn Ngày: 29-02-2024 Lớp 8

568

Toptailieu biên soạn và giới thiệu lời Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Sgk Toán 8 Bài 7 từ đó học tốt môn Toán 8.

Nội dung bài viết

HĐ 1 trang 34 Toán 8 Tập 1
Luyện tập 1 trang 35 Toán 8 Tập 1
Luyện tập 2 trang 35 Toán 8 Tập 1
HĐ 2 trang 35 Toán 8 Tập 1
Luyện tập 3 trang 35 Toán 8 Tập 1
Luyện tập 4 trang 36 Toán 8 Tập 1
Vận dụng trang 36 Toán 8 Tập 1
Bài 2.7 trang 36 Toán 8 Tập 1
Bài 2.8 trang 36 Toán 8 Tập 1
Bài 2.9 trang 36 Toán 8 Tập 1
Bài 2.10 trang 36 Toán 8 Tập 1
Bài 2.11 trang 36 Toán 8 Tập 1

Toán 8 (Kết nối tri thức) Bài 7: Lập phương của một tổng. Lập phương của một hiệu

1. Lập phương của một tổng

HĐ 1 trang 34 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính

$(a + b) {(a + b)}^{2}$

Từ đó rút ra liên hệ giữa ${(a + b)}^{3}$ và $a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ .

Lời giải:

$\begin{array}{l} (a + b) {(a + b)}^{2} = (a + b) . (a^{2} + 2 a b + b^{2}) \\ = a . a^{2} + a .2 a b + a . b^{2} + b . a^{2} + b .2 a b + b . b^{2} \\ = a^{3} + 2 a^{2} b + a b^{2} + a^{2} b + 2 a b^{2} + b^{3} \\ = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} \end{array}$

Giải Toán 8 trang 35

Luyện tập 1 trang 35 Toán 8 Tập 1: 1. Khai triển:

a) ${(x + 3)}^{3}$

b) ${(x + 2 y)}^{3}$

2. Rút gọn biểu thức ${(2 x + y)}^{3} - 8 x^{3} - y^{3}$

Lời giải:

1. a)

${(x + 3)}^{3} = x^{3} + 3. x^{2} .3 + 3. x {.3}^{2} + 3^{3} = x^{3} + 9 x^{2} + 27 x + 27$

${(x + 2 y)}^{3} = x^{3} + 3. x^{2} .2 y + 3. x . {(3 y)}^{2} + {(3 y)}^{3} = x^{3} + 6 x^{2} y + 27 x y^{2} + 27 y^{3}$

$\begin{array}{l} {(2 x + y)}^{3} - 8 x^{3} - y^{3} \\ = {(2 x)}^{3} + 3. {(2 x)}^{2} . y + 3.2 x . y^{2} + y^{3} - 8 x^{3} - y^{3} \\ = 8 x^{2} + 12 x^{2} y + 6 x y^{2} + y^{3} - 8 x^{3} - y^{3} \\ = (8 x^{2} - 8 x^{2}) + 12 x^{2} y + 6 x y^{2} + (y^{3} - y^{3}) \\ = 12 x^{2} y + 6 x y^{2} \end{array}$

Luyện tập 2 trang 35 Toán 8 Tập 1: Viết biểu thức $x^{3} + 9 x^{2} y + 27 x y^{2} + 27 y^{3}$ dưới dạng lập phương của một tổng.

Lời giải:

$\begin{array}{l} x^{3} + 9 x^{2} y + 27 x y^{2} + 27 y^{3} \\ = x^{3} + 3. x^{2} .3 y + 3. x . {(3 y)}^{2} + {(3 y)}^{3} \\ = {(x + 3 y)}^{3} \end{array}$

2. Lập phương của một hiệu

HĐ 2 trang 35 Toán 8 Tập 1: Với hai số $a, b$ bất kì, viết $a - b = a + (- b)$ và áp dụng hằng đẳng thức lập phương của một tổng để tính ${(a - b)}^{3}$ .

Từ đó rút ra liên hệ giữa ${(a - b)}^{3}$ và $a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$ .

Lời giải:

${(a - b)}^{3} = {[a + (- b)]}^{3} = a^{3} + 3. a^{2} . (- b) + 3. a . {(- b)}^{2} + {(- b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$

Từ đó ta có ${(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$

Luyện tập 3 trang 35 Toán 8 Tập 1: Khai triển ${(2 x - y)}^{3}$

Lời giải:

${(2 x - y)}^{3} = {(2 x)}^{3} - 3. {(2 x)}^{2} . y + 3.2 x . y^{2} - y^{3} = 8 x^{3} - 12 x^{2} y + 6 x y^{2} - y^{3}$

Giải Toán 8 trang 36

Luyện tập 4 trang 36 Toán 8 Tập 1: Viết biểu thức sau dưới dạng lập phương của một hiệu

$8 x^{3} - 36 x^{2} y + 54 x y^{2} - 27 y^{3}$ .

Lời giải:

$\begin{array}{l} 8 x^{3} - 36 x^{2} y + 54 x y^{2} - 27 y^{3} \\ = {(2 x)}^{3} - 3. {(2 x)}^{2} .3 y + 3. (2 x) . {(3 y)}^{2} - {(3 y)}^{3} \\ = {(2 x - 3 y)}^{3} \end{array}$

Vận dụng trang 36 Toán 8 Tập 1: Rút gọn biểu thức

${(x - y)}^{3} + {(x + y)}^{3}$ .

Lời giải:

$\begin{array}{l} {(x - y)}^{3} + {(x + y)}^{3} = x^{3} - 3 x^{2} y + 3 x y^{2} - y^{3} + x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3} \\ = (x^{3} + x^{3}) + (- 3 x^{2} y + 3 x^{2} y) + (3 x y^{2} + 3 x y^{2}) + (- y^{3} + y^{3}) \\ = 2 x^{3} + 6 x y^{2} \end{array}$

Bài tập

Bài 2.7 trang 36 Toán 8 Tập 1: Khai triển:

a) ${(x^{2} + 2 y)}^{3}$ ;

b) ${(\frac{1}{2} x - 1)}^{3}$ .

Lời giải:

$\begin{array}{l} {(x^{2} + 2 y)}^{3} = {(x^{2})}^{3} + 3. {(x^{2})}^{2} .2 y + 3. x^{2} . {(2 y)}^{2} + {(2 y)}^{3} \\ = x^{6} + 6 x^{4} y + 12 x^{2} y^{2} + 8 y^{3} \end{array}$

${(\frac{1}{2} x - 1)}^{3} = {(\frac{1}{2} x)}^{3} - 3. {(\frac{1}{2} x)}^{2} .1 + 3. \frac{1}{2} x {.1}^{2} - 1^{3} = \frac{1}{8} x^{3} - \frac{3}{4} x^{2} + \frac{3}{2} x - 1$

Bài 2.8 trang 36 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.

a) $27 + 54 x + 36 x^{2} + 8 x^{3}$ .

Lời giải:

a) $27 + 54 x + 36 x^{2} + 8 x^{3} = 3^{3} + {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} + {(2 x)}^{3} = {(3 + 2 x)}^{3}$

Bài 2.9 trang 36 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:

a) $x^{3} + 9 x^{2} + 27 x + 27$ tại x=7.

b) $27 - 54 x + 36 x^{2} - 8 x^{3}$ tại x=6,5.

Lời giải:

a) $x^{3} + 9 x^{2} + 27 x + 27 = x^{3} + 3. x^{2} .3 + 3. x {.3}^{2} + 3^{3} = {(x + 3)}^{3}$

Thay x=7 vào biểu thức ta được: ${(7 + 3)}^{3} = 10^{3} = 1000$ .

b) $27 - 54 x + 36 x^{2} - 8 x^{3} = 3^{3} - {3.3}^{2} .2 x + 3.3. {(2 x)}^{2} - {(2 x)}^{3} = {(3 - 2 x)}^{3}$

Thay x=6,5 vào biểu thức ta được: ${(3 - 2.6, 5)}^{3} = {(- 10)}^{3} = - 1000$ .

Bài 2.10 trang 36 Toán 8 Tập 1: Rút gọn các biểu thức sau:

a) ${(x - 2 y)}^{3} + {(x + 2 y)}^{3}$

b) ${(3 x + 2 y)}^{3} + {(3 x - 2 y)}^{3}$

Lời giải:

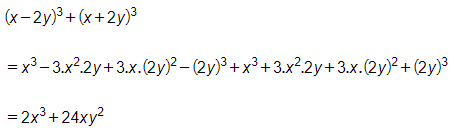
Toán 8 Bài 7 (Kết nối tri thức): Lập phương của một tổng. Lập phương của một hiệu (ảnh 1)

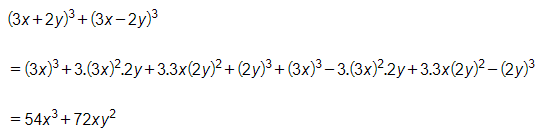
Bài 2.11 trang 36 Toán 8 Tập 1: Chứng minh ${(a - b)}^{3} = - {(b - a)}^{3}$

Lời giải:

$\begin{array}{l} {(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \\ - {(b - a)}^{3} = - (b^{3} - 3 b^{2} a + 3 b a^{2} - a^{3}) \\ = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3} \end{array}$

Vậy ${(a - b)}^{3} = - {(b - a)}^{3}$ (đpcm).

Xem thêm các bài giải Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

Bài 8: Tổng và hiệu hai lập phương

Luyện tập chung trang 40

Bài 9: Phân tích đa thức thành nhân tử

Luyện tập chung trang 45