Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ trang 131,132,133,134,135 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 1. Hình trụ - Diện tích xung quanh và thể tích hình trụ
Phần câu hỏi bài 1 trang 131, 132 Vở bài tập toán 9 tập 2
Câu 1
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ. Biết rằng BC = 3 cm; AB = 6 cm. Diện tích xung quanh của một hình trụ bằng:
(A) (B)
(C (D)
Phương pháp giải:
Diện tích xung quanh của hình trụ có bán kính đáy và chiều cao là
Trả lời:
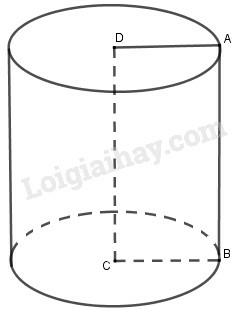
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ có bán kính đáy và chiều cao nên diện tích xung quanh hình trụ là
Chọn C.
Câu 2
Một hình trụ có đường kính đáy d là 12,6 cm, diện tích xung quanh bằng 333,5 cm2. Khi đó, chiều cao h của hình trụ xấp xỉ là (lấy :
(A) 7,9 cm (B) 8,2 cm
(C 8,4 cm (D) 9,2 cm
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
Tính bán kính đáy
Từ công thức tính diện tích xung quanh của hình trụ có bán kính đáy và chiều cao là ta tính được chiều cao
Trả lời:
Bán kính đáy hình trụ là
Gọi chiều cao hình trụ là thì diện tích xung quang hình trụ là
Từ đề bài ta có
Chọn C.
Câu 3
Một hình trụ có thể tích 147,4 cm2, chiều cao 7,5 cm. Nếu làm tròn đến chữ số thập phân thứ hai thì bán kính đáy r của hình trụ xấp xỉ là (lấy ):
(A) 2,2 cm (B) 2,5 cm
(C 2,8 cm (D) 3,2 cm
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
Thể tích hình trụ với là bán kính đáy và là chiều cao hình trụ.
Trả lời:
Gọi là bán kính đáy của hình trụ
Thể tích hình trụ là
Theo đề bài ta có
Chọn B
Một hình trụ có bán kính đáy là , diện tích xung quang bằng . Khi đó chiều cao của hình trụ là:
(A) (B)
(C) (D)
(E) Một kết quả khác
Hãy chọn kết quả đúng
Phương pháp giải:
+ Diện tích xung quanh của hình trụ có bán kính đáy và chiều cao là . Từ đó tính chiều cao hình trụ.
Trả lời
Theo công thức ta có
Vậy kết quả đúng là đáp án E.
Điền đủ kết quả vào những ô trống (...) của bảng sau:
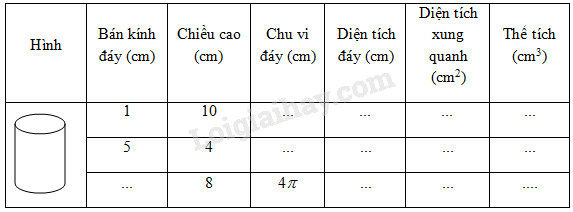
Phương pháp giải:
+ Chu vi đường tròn bán kính là Diện tích hình tròn bán kính là
+ Hình trụ có là bán kính đáy và là chiều cao thì thể tích hình trụ , diện tích xung quanh .
Trả lời:
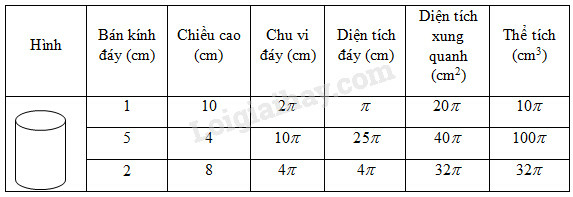
+ Khi và ta có :
- Chu vi đáy : ;
- Diện tích đáy : ;
- Diện tích xung quanh : ;
- Thể tích : .
+ Khi và ta có :
;
; .
+ Khi và chu vi đáy cm ta có :
.
Điền kết quả vào bảng trên.
Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là 2. Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến chữ số thập phân thứ hai).
Phương pháp giải:
+ Hình trụ có là bán kính đáy và là chiều cao thì thể tích hình trụ , diện tích xung quanh .
Trả lời
Theo công thức mà với
Vậy
Theo công thức vì và nên
Cho hình chữ nhật ABCD (AB = 2a, BC = a). Quay hình chữ nhật đó quanh AB thì được được hình trụ có thể tích V1; quanh BC thì được hình trụ có thể tích V2. Trong các đẳng thức dưới đây, hãy chọn đẳng thức đúng.
(A) (B)
(C) (D)
Phương pháp giải:
+ Xác định chiều cao và bán kính đáy của mỗi hình trụ
+ Hình trụ có là bán kính đáy và là chiều cao thì thể tích hình trụ
Trả lời:
Vậy đẳng thức đúng là
Chọn C.
Bài 5 trang 133 Vở bài tập toán 9 tập 2
Người ta nhúng hoàn toàn một tượng đá nhỉ vào một lọ thủy tinh có nước dạng hình trụ. DIện tích đáy của lọ thủy tinh là 2. Nước trong lọ dâng lên thêm . Hỏi thể tích của tượng đá là bao nhiêu ?
Phương pháp giải:
Tính thể tích lượng nước dâng lên bằng công thức với là diện tích đáy và là chiều cao mực nước.
Trả lời:
là thể tích tượng đá. Lượng nước dâng thêm có thể tích bằng thể tích hình trụ có diện tích đáy và chiều cao và bằng thể tích tượng đá. Do đó :
Với và
Vậy thể tích tượng đá là
Điền đủ kết quả những ô trống (...) trong bảng sau:
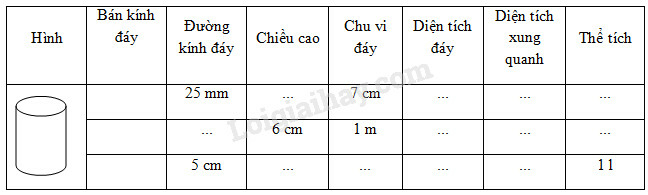
Phương pháp giải:
+ Chu vi đường tròn bán kính là Diện tích hình tròn bán kính là
+ Hình trụ có là bán kính đáy và là chiều cao thì thể tích hình trụ , diện tích xung quanh .
Trả lời:
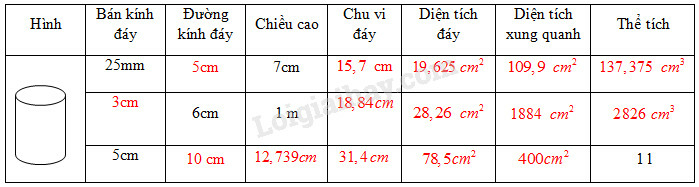
Đổi ;
+ Khi , ta có :
- Đường kính ;
- Chu vi đáy ;
- Diện tích đáy
- Diện tích xung quanh
- Thể tích
+ Khi ta có :
Bán kính :
+ Khi và , ta có :
Đường kính
Chiều cao
Đường ống nối hai bể cá trong một thủy cung ở miền nam nước Pháp có dạng một hình trụ với độ dài . Dung tích của đường ống nói trên là lít. Tính diện tích đáy của đường ống.
Phương pháp giải:
Sử dụng công thức thể tích hình trụ có diện tích đáy và chiều cao là
Trả lời
Ta có : ; lít và
Từ công thức
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.