Với Giải Câu 4 trang 45 VTH Toán 8 Tập 1 lớp 8 trong Bài 10: Tứ giác Vở thực hành Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong Vở thực hành Toán 8.
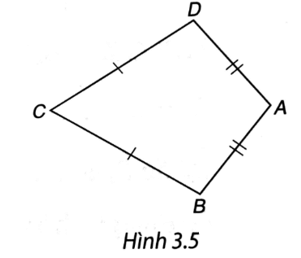
Tứ giác ABCD trong Hình 3.5 có AB = AD, CB = CD được gọi là hình “cái diều”
Bài 4 trang 45 VTH Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.5 có AB = AD, CB = CD được gọi là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Tính các góc B, D biết rằng
Lời giải:
a) Ta có AB = AD, CB = CD nên A, C cách đều B và D, do đó AC là đường trung trực của BD.
b) Cách 1. Nối A và C. Ta có AC là trung trực của BD nên AC là đường phân giác của các góc BCD và BAD.
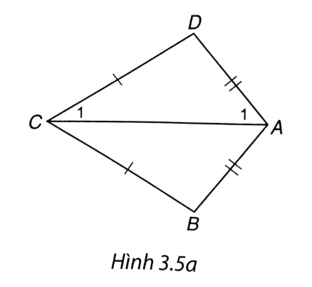Trong có
Tương tự ta cũng có
Cách 2. Nối B, D. Tam giác ABD cân tại đỉnh A nên
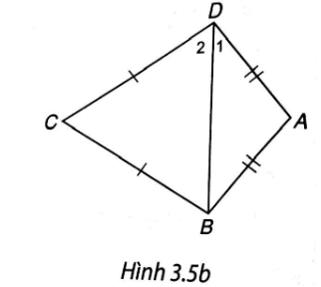
Tam giác CBD cân tại đỉnh C nên
Từ đó
Tương tự ta cũng có
Xem thêm lời giải Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
Câu 1 trang 44 VTH Toán 8 Tập 1: Cho tứ giác ABCD có Khi đó góc B có số đo là
Câu 2 trang 44 VTH Toán 8 Tập 1: Chọn phương án đúng. Cho tứ giác CDEF có số đo các góc như trên Hình 3.1. Khi đó số đo góc D là
Bài 1 trang 44 VTH Toán 8 Tập 1: Tính góc chưa biết của các tứ giác trong Hình 3.2.
Bài 2 trang 45 VTH Toán 8 Tập 1: Tính góc chưa biết của tứ giác trong Hình 3.3, biết rằng
Bài 3 trang 45 VTH Toán 8 Tập 1: Cho tứ giác ABCD trong Hình 3.4, tính số đo x.
Bài 5 trang 46 VTH Toán 8 Tập 1: Cho tứ giác ABCD có
Xem thêm Lời giải bài tập Vở thực hành Toán 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
