Với Giải Bài 3.12 trang 37 sách bài tập Toán 8 Tập 1 trong Bài 12: Hình bình hành Sách bài tập Toán lớp 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 8.
Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng
Bài 3.12 trang 37 sách bài tập Toán 8 Tập 1: Xét hai hình bình hành MNBA và MNCB.
a) Chứng minh A, B, C là ba điểm thẳng hàng;
b) Chứng minh B là trung điểm của AC;
c) Hỏi tam giác MAB thoả mãn điều kiện gì để MNCA là một hình thang cân?
d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thoả mãn điều kiện gì để MNDA là một hình thang cân?
Lời giải:
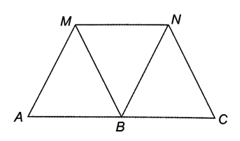
a) Do MNBA và MNCB là hình bình hành
Suy ra AB // MN, BC // MN nên theo tiên đề Euclid, hai đường thẳng AB và BC trùng nhau
Vậy ba điểm A, B, C thẳng hàng.
b) Do MNBA và MNCB là hình bình hành
Suy ra AB = MN, BC = MN
Mà A, B, C thẳng hàng nên B là trung điểm của AC.
c) Do MNCB là hình bình hành nên NC // MB, từ đó (hai góc đồng vị). Điều kiện để hình thang MNCA là hình thang cân là tức là
Vậy điều kiện để MNCA là hình thang cân là tam giác MAB cân tại M.
d)
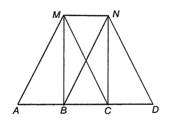
Do MNDC là hình bình hành nên ND // MC, từ đó (hai góc đồng vị). Điều kiện để hình thang MNDA là hình thang cân là .
Vậy điều kiện để MNDA là hình thang cân là tức là tam giác MAC cân tại M.
Do MB là đường trung tuyến của tam giác MAC nên điều kiện để tam giác MAC cân tại M là MB vuông góc với AC.
Vậy điều kiện để hình thang MNDA là hình thang cân đó là tam giác MAB vuông tại B.
Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 3.12 trang 37 sách bài tập Toán 8 Tập 1: Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng;
Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:
SBT Toán 8 (Kết nối tri thức) Bài 11: Hình thang cân
SBT Toán 8 (Kết nối tri thức) Bài 13: Hình chữ nhật
SBT Toán 8 (Kết nối tri thức) Bài 14: Hình thoi và hình vuông
SBT Toán 8 (Kết nối tri thức) Bài tập cuối chương 3
SBT Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.