Với Giải Bài 3.14 trang 37 sách bài tập Toán 8 Tập 1 trong Bài 12: Hình bình hành Sách bài tập Toán lớp 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 8.
Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều
Bài 3.14 trang 37 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều (Gợi ý: Chứng minh các tam giác AEF, DCF, BEC bằng nhau).
Lời giải:
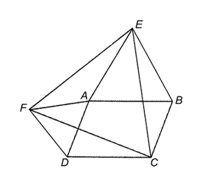
Do ABCD là hình bình hành nên AB // CD
Gọi
Vì AB // CD nên ta có
Suy ra
(do ∆AFD nên ) (1)
• Ta có:
Suy ra
Mà (do ∆AFD và ∆ABE đều)
Suy ra
Từ (1) và (2) suy ra
Xét ∆AEF và ∆DCF có
AF = DF ( vì ∆ADF đều);
(chứng minh trên);
AE = DC (vì cùng bằng AB)
Do đó: ∆AEF = ∆DCF (c.g.c)
Suy ra EF = CF (*)
•
Mà ABCD là hình bình hành nên
Suy ra , mà (chứng minh trên)
Suy ra
Xét ΔBCE và ΔDFC có:
BE = CD (vì cùng bằng AB);
(chứng minh trên);
BC = DF (vì cùng bằng AD)
Do đó ∆BCE = ∆DFC (c.g.c)
Suy ra CE = CF (**)
Từ (*) và (**) suy ra: EF = CF = CE
Vậy ∆ECF là tam giác đều.
Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 3.12 trang 37 sách bài tập Toán 8 Tập 1: Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng;
Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:
SBT Toán 8 (Kết nối tri thức) Bài 11: Hình thang cân
SBT Toán 8 (Kết nối tri thức) Bài 13: Hình chữ nhật
SBT Toán 8 (Kết nối tri thức) Bài 14: Hình thoi và hình vuông
SBT Toán 8 (Kết nối tri thức) Bài tập cuối chương 3
SBT Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.