Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm

Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm

Mai Hương Ngày: 20-01-2024 Lớp 8

377

Với giải Bài 9.46 trang 63 SBT Toán 8 Tập 2 Kết nối tri thức chi tiết trong Bài 36: Các trường hợp đồng dạng của hai tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm

Bài 9.46 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Lời giải:

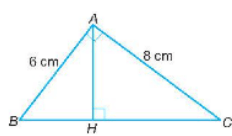
Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 6² + 8² = 100

Nên BC = 10 cm.

Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

$\hat{C}$ chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{A C}{H C} = \frac{B C}{A C}$ nên CH = $\frac{C A^{2}}{C B} = \frac{8^{2}}{10} = \frac{32}{5} = 6, 4$ (cm).

Do đó, BH = BC – CH = 10 – 6,4 = 3,6 (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên $\frac{A B}{H A} = \frac{B C}{A C}$ .

Do đó, AH = $\frac{A B \cdot A C}{B C} = \frac{6 \cdot 8}{10} = 4, 8$ (cm).

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 9.42 trang 62 SBT Toán lớp 8 Tập 2: Những điều kiện nào dưới đây kéo theo hai tam giác vuông đồng dạng.

Bài 9.43 trang 62 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông cân tại A và tam giác MNP có MN = MP = 4 cm và NP = $4 \sqrt{2}$ cm. Chứng minh rằng ∆ABC ᔕ ∆MNP.

Bài 9.44 trang 63 SBT Toán lớp 8 Tập 2: Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng ?

Bài 9.45 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:

Bài 9.46 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Bài 9.47 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:

Bài 9.48 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:

Bài 9.49 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC

Bài 9.50 trang 64 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD như Hình 9.11. Biết rằng $\hat{B A D} = \hat{B D C} = 90 °$ , AD = 4 cm, BD = 6 cm và BC = 9

Bài 9.51 trang 64 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC.

Bài 9.52 trang 64 SBT Toán lớp 8 Tập 2: Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'

Bài 9.53 trang 64 SBT Toán lớp 8 Tập 2: Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác

Bài 35: Định lí Pythagore và ứng dụng

Bài 37: Hình đồng dạng

Bài tập cuối chương 9

Bài 38: Hình chóp tam giác đều

Bài 39: Hình chóp tứ giác đều

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

397

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

428

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

429

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

386

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.