Với giải Bài 9.51 trang 64 SBT Toán 8 Tập 2 Kết nối tri thức chi tiết trong Bài 36: Các trường hợp đồng dạng của hai tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC
Bài 9.51 trang 64 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:
a) AM . AB = AH2 và AM . AB = AN . AC.
b) ∆AMN ᔕ ∆ACB.
Lời giải:
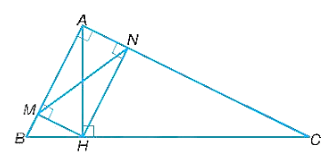
a) Tam giác AMH vuông ở M và tam giác AHB vuông ở H có:
chung
Do đó, ∆AMH ᔕ ∆AHB (góc nhọn).
Suy ra nên AM . AB = AH2 (1).
Tam giác ANH vuông ở N và tam giác AHC vuông ở H có:
chung
Do đó, ∆ANH ᔕ ∆AHC (góc nhọn).
Suy ra nên AN . AC = AH2 (2).
Từ (1) và (2) ta có: AM . AB = AN . AC.
b) Theo phần a ta có: AM . AB = AN . AC nên .
Tam giác AMN và tam giác ACB có:
chung
Do đó, ∆AMN ᔕ ∆ACB (c.g.c).
Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 9.42 trang 62 SBT Toán lớp 8 Tập 2: Những điều kiện nào dưới đây kéo theo hai tam giác vuông đồng dạng.
Bài 9.43 trang 62 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông cân tại A và tam giác MNP có MN = MP = 4 cm và NP = cm. Chứng minh rằng ∆ABC ᔕ ∆MNP.
Bài 9.44 trang 63 SBT Toán lớp 8 Tập 2: Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng ?
Bài 9.45 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:
Bài 9.46 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.
Bài 9.47 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
Bài 9.48 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:
Bài 9.49 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC
Bài 9.50 trang 64 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD như Hình 9.11. Biết rằng , AD = 4 cm, BD = 6 cm và BC = 9
Bài 9.51 trang 64 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC.
Bài 9.52 trang 64 SBT Toán lớp 8 Tập 2: Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'
Bài 9.53 trang 64 SBT Toán lớp 8 Tập 2: Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.
Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác
Bài 35: Định lí Pythagore và ứng dụng
Bài 37: Hình đồng dạng
Bài tập cuối chương 9
Bài 38: Hình chóp tam giác đều
Bài 39: Hình chóp tứ giác đều
