Toán 9 (Kết nối tri thức) Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Mai Hương Ngày: 07-03-2024 Lớp 9

Toptailieu biên soạn và giới thiệu lời giải Toán 9 (Kết nối tri thức) Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 9 Bài 1 từ đó học tốt môn Toán 9.

Toán 9 (Kết nối tri thức) Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

HĐ1

Hoạt động 1 trang 6 Toán 9 Tập 1: Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.

Lời giải:

Hệ thức biểu thị: $x + y = 17.$

HĐ2

Hoạt động 2 trang 6 Toán 9 Tập 1: Tương tự, hãy viết hệ thức với hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.

Quýt, cam mười bảy quả tươi

Đem chia cho một trăm người cùng vui.

Chia ba mỗi quả quýt rồi,

Còn cam, mỗi quả chia mười vừa xinh.

Trăm người, trăm miếng ngọt lành.

Quýt, cam mỗi loại tính rành là bao?

Lời giải:

Hệ thức liên hệ giữa x và y qua các câu thơ thứ ba, thứ tư và thứ năm là $3 x + 10 y = 100.$

LT1

Luyện tập 1 trang 6 Toán 9 Kết nối tri thức Tập 1: Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.

Lời giải:

Ta có $2 x - y = 5$ là một phương trình bậc nhất hai ẩn.

Cặp số $(3; 1)$ là một nghiệm của phương trình $2 x - y = 5$ vì $2.3 - 1 = 5.$ (luôn đúng).

LT2

Luyện tập 2 trang 8 Toán 9 Kết nối tri thức Tập 1: Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) $2 x - 3 y = 5;$

b) $0 x + y = 3;$

c) $x + 0 y = - 2.$

Lời giải:

a) $2 x - 3 y = 5;$

Ta có $y = \frac{2 x + 5}{3} = \frac{2 x}{3} + \frac{5}{3}$ nên mỗi cặp số $(x; \frac{2 x}{3} + \frac{5}{3})$ với $x \in R$ tùy ý là một nghiệm của phương trình $2 x - 3 y = 5.$

Biểu diễn hình học tất cả các nghiệm của phương trình $2 x - 3 y = 5.$

Cho $x = 0 \Rightarrow y = \frac{- 5}{3} \Rightarrow A (0; \frac{- 5}{3})$

$y = 0 \Rightarrow x = \frac{5}{2} \Rightarrow B (\frac{5}{2}; 0)$

Đường thẳng $2 x - 3 y = 5$ đi qua hai điểm A và B

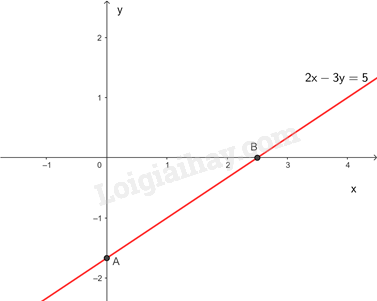
Các nghiệm là tọa độ của một điểm thuộc đường thẳng $2 x - 3 y = 5.$

b) $0 x + y = 3;$

Ta có $0 x + y = 3$ rút gọn thành $y = 3$ nên phương trình có nghiệm là $(x; 3)$ với $x \in R$ tùy ý.

Biểu diễn hình học tất cả các nghiệm của phương trình $0 x + y = 3$

Cho $x = 0 \Rightarrow y = 3 \Rightarrow A (0; 3)$

$x = 1 \Rightarrow y = 3 \Rightarrow B (1; 3)$

Đường thẳng $0 x + y = 3$ đi qua hai điểm A và B

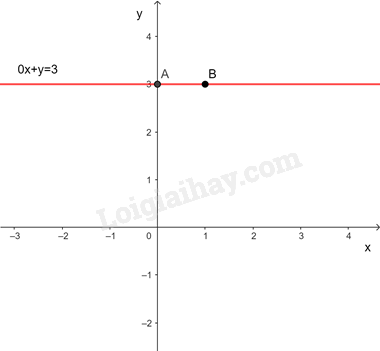
Các nghiệm là tọa độ của một điểm thuộc đường thẳng $0 x + y = 3.$

c) $x + 0 y = - 2.$

Ta có $x + 0 y = - 2$ rút gọn thành $x = - 2$ nên phương trình có nghiệm là $(- 2; y)$ với $y \in R$ tùy ý.

Biểu diễn hình học tất cả các nghiệm của phương trình $x + 0 y = - 2$

Cho $y = 0 \Rightarrow x = - 2 \Rightarrow A (- 2; 0)$

$y = 1 \Rightarrow x = - 2 \Rightarrow B (- 2; 1)$

Đường thẳng $x + 0 y = - 2$ đi qua hai điểm A và B

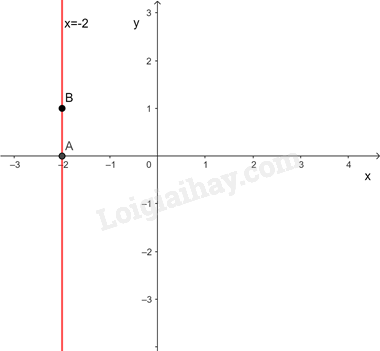
Các nghiệm là tọa độ của một điểm thuộc đường thẳng $x + 0 y = - 2.$

LT3

Luyện tập 3 trang 9 Toán 9 Kết nối tri thức Tập 1: Trong hai cặp số $(0; - 2)$ và $(2; - 1),$ cặp số nào là nghiệm của hệ phương trình

${\begin{cases} x - 2 y = 4 \\ 4 x + 3 y = 5 \end{cases} ?$

Lời giải:

Thay $(0; - 2)$ vào hệ đã cho ta có:

${\begin{cases} 0 - 2. (- 2) = 4 \\ 4.0 + 3 (- 2) = 5 \end{cases}$ (vô lí)

Nên $(0; - 2)$ không là nghiệm của hệ phương trình đã cho.

Thay $(2; - 1)$ vào hệ đã cho ta có:

${\begin{cases} 2 - 2. (- 1) = 4 \\ 4.2 + 3 (- 1) = 5 \end{cases}$ (luôn đúng)

Nên $(2; - 1)$ là nghiệm của hệ phương trình đã cho.

Vận dụng trang 9 Toán 9 Kết nối tri thức Tập 1: Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính $(x; y \in N^{*}),$ ta có hệ phương trình bậc nhất hai ẩn sau:

${\begin{cases} x + y = 17 \\ 10 x + 3 y = 100 \end{cases}$

Trong hai cặp số $(10; 7)$ và $(7; 10),$ cặp số nào là nghiệm của hệ phương trỉnh trên? Từ đó cho biết phương án về số cam và số quýt thỏa mãn yêu cầu của bài toán cổ.

Lời giải:

Thay $(10; 7)$ vào hệ đã cho ta có:

${\begin{cases} 10 + 7 = 17 \\ 10.10 + 3.7 = 100 \end{cases}$ (vô lí)

Nên $(10; 7)$ không là nghiệm của hệ phương trình đã cho.

Thay $(7; 10)$ vào hệ đã cho ta có:

${\begin{cases} 7 + 10 = 17 \\ 10.7 + 3.10 = 100 \end{cases}$ (luôn đúng)

Nên $(7; 10)$ là nghiệm của hệ phương trình đã cho.

Vậy số quả quýt là 7 quả, số quả cam là 10 quả.

Bài 1.1 trang 10 Toán 9 Tập 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn, vì sao?

a) $5 x - 8 y = 0;$

b) $4 x + 0 y = - 2;$

c) $0 x + 0 y = 1;$

d) $0 x - 3 y = 9.$

Lời giải:

a) Là phương trình bậc nhất vì phương trình có dạng $a x + b y = c$ và $a = 5; b = - 8$ thỏa mãn điều kiện $a \neq 0$ hoặc $b \neq 0.$

b) Là phương trình bậc nhất vì phương trình có dạng $a x + b y = c$ và $a = 4; b = 0$ thỏa mãn điều kiện $a \neq 0$ hoặc $b \neq 0.$

c) Không là phương trình bậc nhất vì phương trình có hệ số $a = 0; b = 0$ không thỏa mãn điều kiện $a \neq 0$ hoặc $b \neq 0.$

d) Là phương trình bậc nhất vì phương trình có dạng $a x + b y = c$ và $a = 0; b = - 3$ thỏa mãn điều kiện $a \neq 0$ hoặc $b \neq 0.$

Bài 1.2 trang 10 Toán 9 Tập 1:

a) Tìm giá trị thích hợp thay cho dấu “?” trong bảng sau rồi cho biết 6 nghiệm của phương trình $2 x - y = 1 :$

b) Viết nghiệm tổng quát của phương trình đã cho.

Lời giải:

Các cặp nghiệm của phương trình $y = 2 x - 1$ là: $(- 1; - 3); (- 0, 5; - 2); (0; - 1); (0, 5; 0); (1; 1); (2; 3) .$

b) Ta có: $2 x - y = 1 \Rightarrow y = 2 x - 1$ nên cặp số $(x; 2 x - 1)$ với $x \in R$ tùy ý là nghiệm tổng quát của phương trình $2 x - y = 1.$

Bài 1.3 trang 10 Toán 9 Tập 1: Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) $2 x - y = 3;$

b) $0 x + 2 y = - 4;$

c) $3 x + 0 y = 5.$

Lời giải:

a) $2 x - y = 3$

Ta có $y = 2 x - 3$ nên mỗi cặp số $(x; 2 x - 3)$ với $x \in R$ tùy ý là một nghiệm của phương trình $2 x - y = 3.$

Biểu diễn hình học tất cả các nghiệm của phương trình $2 x - y = 3$

Cho $x = 0 \Rightarrow y = - 3 \Rightarrow A (0; - 3)$

$y = 0 \Rightarrow x = \frac{3}{2} \Rightarrow B (\frac{3}{2}; 0)$

Đường thẳng $2 x - y = 3$ đi qua hai điểm A và B

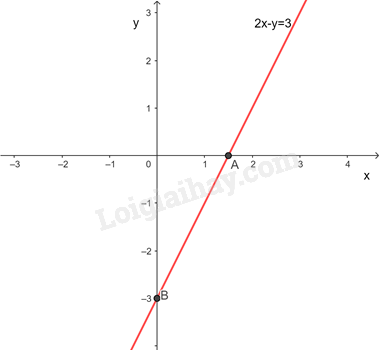
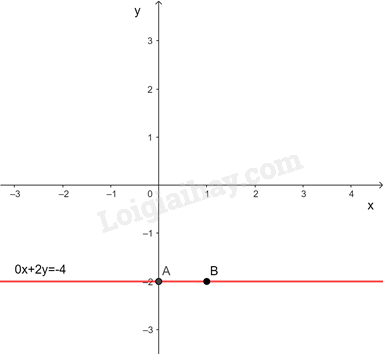
b) $0 x + 2 y = - 4$

Ta có $0 x + 2 y = - 4 \Rightarrow y = - 2$ nên mỗi cặp số $(x; - 2)$ với $x \in R$ tùy ý là một nghiệm của phương trình $0 x + 2 y = - 4$

Biểu diễn hình học tất cả các nghiệm của phương trình $0 x + 2 y = - 4$

Cho $x = 0 \Rightarrow y = - 2 \Rightarrow A (0; - 2)$

$x = 1 \Rightarrow y = - 2 \Rightarrow B (1; - 2)$

Đường thẳng $0 x + 2 y = - 4$ đi qua hai điểm A và B

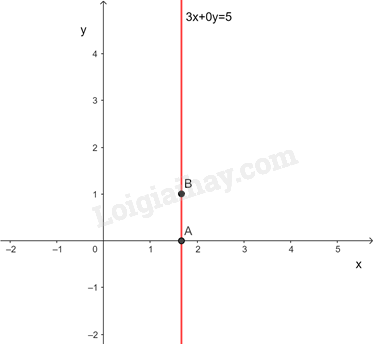
c) $3 x + 0 y = 5$

Ta có $3 x + 0 y = 5 \Rightarrow x = \frac{5}{3}$ nên mỗi cặp số $(\frac{5}{3}; y)$ với $y \in R$ tùy ý là một nghiệm của phương trình $3 x + 0 y = 5$

Biểu diễn hình học tất cả các nghiệm của phương trình $3 x + 0 y = 5$

Cho $y = 1 \Rightarrow x = \frac{5}{3} \Rightarrow A (\frac{5}{3}; 1)$

$y = 0 \Rightarrow x = \frac{5}{3} \Rightarrow B (\frac{5}{3}; 0)$

Đường thẳng $3 x + 0 y = 5$ đi qua hai điểm A và B

Bài 1.4 trang 10 Toán 9 Tập 1:

a) Hệ phương trình ${\begin{cases} 2 x = - 6 \\ 5 x + 4 y = 1 \end{cases}$ có là một hệ hai phương trình bậc nhất hai ẩn không, vì sao?

b) Cặp số $(- 3; 4)$ có là một nghiệm của hệ phương trình đó hay không, vì sao?

Lời giải:

a) Hệ phương trình đã cho là hệ phương trình bậc nhất hai ẩn vì $2 x = - 6$ và $5 x + 4 y = 1$ là hai phương trình bậc nhất 2 ẩn thỏa mãn điều kiện $a \neq 0$ hoặc $b \neq 0.$

b) Thay $(- 3; 4)$ vào hệ phương trình ta có ${\begin{cases} 2. (- 3) = - 6 \\ 5. (- 3) + 4.4 = 1 \end{cases}$ (luôn đúng)

Vậy $(- 3; 4)$ là nghiệm của hệ phương trình.

Bài 1.5 trang 10 Toán 9 Tập 1:

Cho các cặp số $(- 2; 1), (0; 2), (1; 0), (1, 5; 3), (4; - 3)$ và hai phương trình

$\begin{array}{l} 5 x + 4 y = 8, (1) \\ 3 x + 5 y = - 3. (2) \end{array}$

Trong các cặp số đã cho:

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?

c) Vẽ hai đường thẳng $5 x + 4 y = 8$ và $3 x + 5 y = - 3$ trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.

Lời giải:

a) Thay $(- 2; 1)$ vào phương trình (1) ta có: $5. (- 2) + 4.1 = 8$ (vô lí)

Thay $(0; 2)$ vào phương trình (1) ta có: $5.0 + 4.2 = 8$ (luôn đúng)

Thay $(1; 0)$ vào phương trình (1) ta có: $5.1. + 4.0 = 8$ (vô lí)

Thay $(1, 5; 3)$ vào phương trình (1) ta có: $5.1, 5 + 4.0 = 8$ (vô lí)

Thay $(4; - 3)$ vào phương trình (1) ta có: $5.4 + 4. (- 3) = 8$ (luôn đúng)

Vậy nghiệm của phương trình (1) là $(0; 2)$ và $(4; - 3) .$

b) Vì $(- 2; 1)$ , $(1; 0)$ và $(1, 5; 3)$ không là nghiệm của phương trình (1) nên cũng không là nghiệm của hệ phương trình gồm (1) và (2).

Thay $(0; 2)$ vào phương trình (2) ta có: $3.0 + 5.2 = - 3$ (vô lí).

Thay $(4; - 3)$ vào phương trình (2) ta có: $3.4 + 5. (- 3) = - 3$ (luôn đúng).

Vậy $(4; - 3)$ là nghiệm của hệ phương trình gồm (1) và (2).

c) Đường thẳng $5 x + 4 y = 8$

Cho $x = 0 \Rightarrow y = 2 \Rightarrow A (0; 2)$

$y = 0 \Rightarrow x = \frac{8}{5} \Rightarrow B (\frac{8}{5}; 0)$

Đường thẳng $5 x + 4 y = 8$ đi qua điểm A và B

Đường thẳng $3 x + 5 y = - 3$

Cho $x = 0 \Rightarrow y = \frac{- 3}{5} \Rightarrow C (0; \frac{- 3}{5})$

$y = 0 \Rightarrow x = - 1 \Rightarrow D (- 1; 0)$

Đường thẳng $3 x + 5 y = - 3$ đi qua điểm C và D

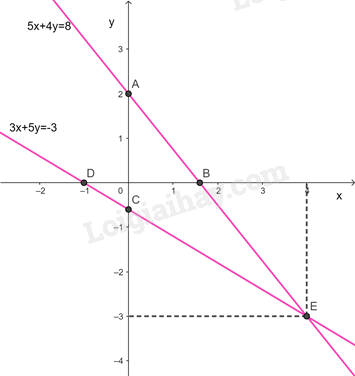
Ta có điểm $E (4; - 3)$ là giao điểm của đường thẳng $5 x + 4 y = 8$ và đường thẳng $3 x + 5 y = - 3$ nên $(4; - 3)$ là nghiệm của hệ phương trình gồm (1) và (2)