Toán 9 (Chân trời sáng tạo) Bài tập cuối chương 1

Mai Hương Ngày: 07-03-2024 Lớp 9

Toptailieu biên soạn và giới thiệu lời giải Toán 9 (Chân trời sáng tạo) Bài tập cuối chương 1 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 9 Bài tập cuối chương 1 từ đó học tốt môn Toán 9.

Toán 9 (Chân trời sáng tạo) Bài tập cuối chương 1

Bài 1 trang 22 Toán 9 Tập 1: Tất cả các nghiệm của phương trình (x + 3)(2x – 6) = 0 là

Lời giải:

(x + 3)(2x – 6) = 0

x + 3 = 0 hoặc 2x – 6 = 0

suy ra x = -3 hoặc x = 3

Đáp án C

Bài 2 trang 22 Toán 9 Tập 1: Điều kiện xác định của phương trình

\frac{2 x + 3}{x - 4} + 2 = \frac{1}{x - 3}

là

A. x $\neq$ 4

B. x $\neq$ 3

C. x $\neq$ 4 và x $\neq$ 3

D. x = 4 và x = 3

Lời giải:

$\frac{2 x + 3}{x - 4} + 2 = \frac{1}{x - 3}$

ĐKXĐ: ${\begin{matrix} x - 4 \neq 0 \\ x - 3 \neq 0 \end{matrix}$ suy ra ${\begin{matrix} x \neq 4 \\ x \neq 3 \end{matrix}$

Đáp án C.

Bài 3 trang 22 Toán 9 Tập 1: Nghiệm của phương trình $\frac{x + 2}{x - 4} - 1 = \frac{30}{(x + 3) (x - 4)}$ là

Lời giải:

$\frac{x + 2}{x - 4} - 1 = \frac{30}{(x + 3) (x - 4)}$

ĐKXĐ: ${\begin{matrix} x \neq 4 \\ x \neq - 3 \end{matrix}$

(x + 2)(x + 3) – (x + 3)(x – 4) = 30

(x + 3)(x + 2 – x + 4) = 30

(x + 3).6 = 30

x + 3 = 5

x = 2 (TMĐK)

Vậy nghiệm của phương trình là x = 2.

Đáp án A.

Bài 4 trang 22 Toán 9 Tập 1: Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn?

A. 5x - y = 3

B. $\sqrt{5} x + 0 y = 0$

C. $0 x - 4 y = \sqrt{6}$

D. 0x + 0y = 12

Lời giải:

Đáp án D vì a = b = 0.

Bài 5 trang 22 Toán 9 Tập 1: Đường thẳng biểu diễn tất cả các nghiệm của phương trình 3x – y = 2

A. vuông góc với trục tung

B. vuông góc với trục hoành

C. đi qua gốc toạ độ

D. đi qua điểm A(1;1)

Lời giải:

Ta có đường thẳng d: y = 3x – 2.

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = 3x – 2.

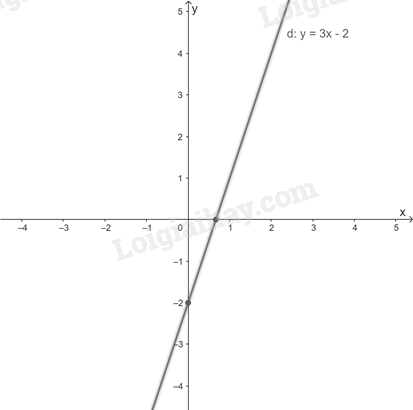
Quan sát đường thẳng d ta thấy d không vuông góc với trục tung và không vuông góc với trục hoành nên A và B sai.

Với x = 0 ta được y = 3.0 – 2 = -2 0 suy ra d không đi qua gốc toạ độ nên C sai.

Với x = 1 ta được y = 3.1 – 2 = 1. Vậy đường thẳng d đi qua điểm A(1;1) nên D đúng.

Đáp án D.

Bài 6 trang 22 Toán 9 Tập 1: Cặp số (-2;-3) là nghiệm của hệ phương trình nào sau đây?

A. ${\begin{matrix} x - 2 y = 3 \\ 2 x + y = 4 \end{matrix}$

B. ${\begin{matrix} 2 x - y = - 1 \\ x - 3 y = 8 \end{matrix}$

C. ${\begin{matrix} 2 x - y = - 1 \\ x - 3 y = 7 \end{matrix}$

D. ${\begin{matrix} 4 x - 2 y = 0 \\ x - 3 y = 5 \end{matrix}$

Lời giải:

Cặp số (-2;-3) không là nghiệm của hệ phương trình ${\begin{matrix} x - 2 y = 3 \\ 2 x + y = 4 \end{matrix}$ vì ${\begin{matrix} (- 2) - 2. (- 3) = 4 \neq 3 \\ 2 (- 2) + (- 3) = - 7 \neq 4 \end{matrix}$ .

Cặp số (-2;-3) không là nghiệm của hệ phương trình ${\begin{matrix} 2 x - y = - 1 \\ x - 3 y = 8 \end{matrix}$ vì ${\begin{matrix} 2. (- 2) - (- 3) = - 1 \\ (- 2) - 3. (- 3) = 7 \neq 8 \end{matrix}$ .

Cặp số (-2;-3) là nghiệm của hệ phương trình ${\begin{matrix} 2 x - y = - 1 \\ x - 3 y = 7 \end{matrix}$ vì ${\begin{matrix} 2. (- 2) - (- 3) = - 1 \\ (- 2) - 3. (- 3) = 7 \end{matrix}$ .

Cặp số (-2;-3) không là nghiệm của hệ phương trình ${\begin{matrix} 4 x - 2 y = 0 \\ x - 3 y = 5 \end{matrix}$ vì ${\begin{matrix} 4. (- 2) - 2. (- 3) = - 2 \neq 0 \\ - 2 - 3. (- 3) = 7 \neq 5 \end{matrix}$ .

Đáp án C.

Bài 7 trang 22 Toán 9 Tập 1: Giải các hệ phương trình:

a) ${\begin{matrix} 3 x + 2 y = 7 \\ x - 7 y = - 13 \end{matrix}$

b) ${\begin{matrix} 4 x + y = 2 \\ 8 x + 3 y = 5 \end{matrix}$

c) ${\begin{matrix} 5 x - 4 y = 3 \\ 2 x + y = 4 \end{matrix}$

d) ${\begin{matrix} 3 x - 2 y = 10 \\ x - \frac{2}{3} y = 3 \frac{1}{3} \end{matrix}$

Lời giải:

a) ${\begin{matrix} 3 x + 2 y = 7 \\ x - 7 y = - 13 \end{matrix}$

$\begin{array}{l} {\begin{matrix} 3. (- 13 + 7 y) + 2 y = 7 \\ x = - 13 + 7 y \end{matrix} \\ {\begin{matrix} 23 y = 46 \\ x = - 13 + 7 y \end{matrix} \\ {\begin{matrix} y = 2 \\ x = 1 \end{matrix} \end{array}$

Vậy nghiệm duy nhất của hệ phương trình là (1;2)

b) ${\begin{matrix} 4 x + y = 2 \\ 8 x + 3 y = 5 \end{matrix}$

$\begin{array}{l} {\begin{matrix} y = 2 - 4 x \\ 8 x + 3. (2 - 4 x) = 5 \end{matrix} \\ {\begin{matrix} y = 2 - 4 x \\ - 4 x = - 1 \end{matrix} \\ {\begin{matrix} y = 1 \\ x = \frac{1}{4} \end{matrix} \end{array}$

Vậy nghiệm duy nhất của hệ phương trình là $(\frac{1}{4}; 1)$ .

c) ${\begin{matrix} 5 x - 4 y = 3 \\ 2 x + y = 4 \end{matrix}$

$\begin{array}{l} {\begin{matrix} 5 x - 4. (4 - 2 x) = 3 \\ y = 4 - 2 x \end{matrix} \\ {\begin{matrix} 13 x = 19 \\ y = 4 - 2 x \end{matrix} \\ {\begin{matrix} x = \frac{19}{13} \\ y = \frac{14}{13} \end{matrix} \end{array}$

Vậy nghiệm duy nhất của hệ phương trình là $(\frac{19}{13}; \frac{14}{13})$

d) ${\begin{matrix} 3 x - 2 y = 10 \\ x - \frac{2}{3} y = 3 \frac{1}{3} \end{matrix}$

$\begin{array}{l} {\begin{matrix} 3 x - 2 y = 10 \\ x = 3 \frac{1}{3} + \frac{2}{3} y = \frac{10}{3} + \frac{2}{3} y \end{matrix} \\ {\begin{matrix} 3. (\frac{10}{3} + \frac{2}{3} y) - 2 y = 10 \\ x = 3 \frac{1}{3} + \frac{2}{3} y = \frac{10}{3} + \frac{2}{3} y \end{matrix} \\ {\begin{matrix} 3. (\frac{10}{3} + \frac{2}{3} y) - 2 y = 10 \\ x = \frac{10}{3} + \frac{2}{3} y \end{matrix} \\ {\begin{matrix} 0 y = 0 \\ x = \frac{10}{3} + \frac{2}{3} y \end{matrix} \end{array}$

Phương trình 0y = 0 nghiệm đúng với mọi x $\in R$ .

Vậy hệ phương trình có vô số nghiệm. Các nghiệm của hệ được viết như sau: ${\begin{matrix} y \in R \\ x = \frac{10}{3} + \frac{2}{3} y \end{matrix}$

Bài 8 trang 22 Toán 9 Tập 1: Giải các phương trình:

a) (5x + 2)(2x – 7) = 0

b) $(\frac{1}{2} x + 5) (- \frac{2}{3} x - \frac{4}{3}) = 0$

c) $y^{2} - 5 y + 2 (y - 5) = 0$

d) $9 x^{2} - 1 = (3 x - 1) (2 x + 7)$

Lời giải:

a) (5x + 2)(2x – 7) = 0

$\begin{array}{l} [\begin{matrix} 5 x + 2 = 0 \\ 2 x - 7 = 0 \end{matrix} \\ [\begin{matrix} x = \frac{- 2}{5} \\ x = \frac{7}{2} \end{matrix} \end{array}$

Vậy phương trình có nghiệm là: x = $\frac{- 2}{5}$ hoặc x = $\frac{7}{2}$ .

b) $(\frac{1}{2} x + 5) (- \frac{2}{3} x - \frac{4}{3}) = 0$

$\begin{array}{l} [\begin{matrix} \frac{1}{2} x + 5 = 0 \\ - \frac{2}{3} x - \frac{4}{3} = 0 \end{matrix} \\ [\begin{matrix} x = - 10 \\ x = - 2 \end{matrix} \end{array}$

Vậy phương trình có nghiệm là: x = -10 hoặc x = -2.

c) $y^{2} - 5 y + 2 (y - 5) = 0$

$\begin{array}{l} y (y - 5) + 2 (y - 5) = 0 \\ (y - 5) (y + 2) = 0 \end{array}$

$\begin{array}{l} [\begin{matrix} y - 5 = 0 \\ y + 2 = 0 \end{matrix} \\ [\begin{matrix} y = 5 \\ y = - 2 \end{matrix} \end{array}$

Vậy nghiệm của phương trình là y = -2 hoặc y = 5

d) $9 x^{2} - 1 = (3 x - 1) (2 x + 7)$

$\begin{array}{l} 9 x^{2} - 1 = (3 x - 1) (2 x + 7) \\ (3 x - 1) (3 x + 1) - (3 x - 1) (2 x + 7) = 0 \\ (3 x - 1) (3 x + 1 - 2 x - 7) = 0 \\ (3 x - 1) (x - 6) = 0 \\ [\begin{matrix} 3 x - 1 = 0 \\ x - 6 = 0 \end{matrix} \\ [\begin{matrix} x = \frac{1}{3} \\ x = 6 \end{matrix} \end{array}$

Vậy nghiệm của phương trình là x = 6 hoặc x = $\frac{1}{3}$ .

Bài 9 trang 22 Toán 9 Tập 1: Giải các phương trình:

a) $\frac{5}{x + 2} + \frac{3}{x - 1} = \frac{3 x + 4}{(x + 2) (x - 1)}$

b) $\frac{4}{2 x - 3} - \frac{3}{x (2 x - 3)} = \frac{5}{x}$

c) $\frac{2}{x - 3} + \frac{3}{x + 3} = \frac{3 x - 5}{x^{2} - 9}$

d) $\frac{x - 1}{x + 1} - \frac{x + 1}{x - 1} = \frac{8}{x^{2} - 1}$

Lời giải:

a) $\frac{5}{x + 2} + \frac{3}{x - 1} = \frac{3 x + 4}{(x + 2) (x - 1)}$

ĐKXĐ: ${\begin{matrix} x \neq - 2 \\ x \neq 1 \end{matrix}$

$\frac{5}{x + 2} + \frac{3}{x - 1} = \frac{3 x + 4}{(x + 2) (x - 1)}$

$\frac{5 (x - 1)}{(x + 2) (x - 1)} + \frac{3 (x + 2)}{(x + 2) (x - 1)} = \frac{3 x + 4}{(x + 2) (x - 1)}$

5(x – 1) + 3(x + 2) = 3x + 4

5x – 5 + 3x + 6 = 3x + 4

5x = 3

x = $\frac{3}{5}$ (TMĐK)

Vậy nghiệm của phương trình là: x = $\frac{3}{5}$ .

b) $\frac{4}{2 x - 3} - \frac{3}{x (2 x - 3)} = \frac{5}{x}$

ĐKXĐ: ${\begin{matrix} x \neq 0 \\ x \neq \frac{3}{2} \end{matrix}$

$\frac{4}{2 x - 3} - \frac{3}{x (2 x - 3)} = \frac{5}{x}$

$\frac{4 x}{2 x - 3} - \frac{3}{x (2 x - 3)} = \frac{5 (2 x - 3)}{x}$

4x – 3 = 5(2x – 3)

4x – 3 = 10x – 15

6x = 12

x = 2 (TMĐK)

Vậy nghiệm của phương trình là: x = 2.

c) $\frac{2}{x - 3} + \frac{3}{x + 3} = \frac{3 x - 5}{x^{2} - 9}$

ĐKXĐ: ${\begin{matrix} x \neq 3 \\ x \neq - 3 \end{matrix}$

$\frac{2}{x - 3} + \frac{3}{x + 3} = \frac{3 x - 5}{x^{2} - 9}$

$\frac{2 (x + 3)}{x - 3} + \frac{3 (x - 3)}{x + 3} = \frac{3 x - 5}{(x - 3) (x + 3)}$

2(x + 3) + 3(x – 3) = 3x – 5

2x + 6 + 3x – 9 = 3x – 5

2x = - 2

x = - 1 (TMĐK)

Vậy nghiệm của phương trình là: x = -1.

d) $\frac{x - 1}{x + 1} - \frac{x + 1}{x - 1} = \frac{8}{x^{2} - 1}$

ĐKXĐ: ${\begin{matrix} x \neq 1 \\ x \neq - 1 \end{matrix}$

$\frac{x - 1}{x + 1} - \frac{x + 1}{x - 1} = \frac{8}{x^{2} - 1}$

$\frac{{(x - 1)}^{2}}{x + 1} - \frac{{(x + 1)}^{2}}{x - 1} = \frac{8}{(x - 1) (x + 1)}$

${(x - 1)}^{2} - {(x + 1)}^{2} = 8$

x2 – 2x + 1 – (x2 + 2x + 1) = 8

-4x = 8

x = - 2 (TMĐK)

Vậy nghiệm của phương trình là: x = -2.

Bài 10 trang 23 Toán 9 Tập 1: Tìm hai số nguyên dương biết tổng của chúng bằng 1006, nếu lấy số lớn chia cho số bé được thương là 2 và số dư là 124.

Lời giải:

Gọi x và y lần lượt là số lớn và số bé cần tìm ( $x \in N *; y \in N *$ ).

Tổng của chúng bằng 1006, nên ta có phương trình: x + y = 1006 (1)

Lấy số lớn chia cho số bé được thương là 2 và số dư là 124, nên ta có phương trình: x = 2y + 124 (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} x + y = 1006 \\ x - 2 y = 124 \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 712 \\ y = 294 \end{matrix}$

Vậy số lớn là 712, số bé là 294.

Bài 11 trang 23 Toán 9 Tập 1: Ở giải bóng đá Ngoại hạng Anh mùa giải 2003 – 2004, đội Arsenal đã thi đấu 38 trận mà không thua trận nào và giành chức vô địch với 90 điểm. Biết rằng với mỗi trận đấu, đội thắng được 3 điểm, đội thua không có điểm và nếu hai đội hoà nhau thì mỗi đội được 1 điểm. Mùa giải đó đội Arsenal đã giành bao nhiêu trận thắng?

Lời giải:

Gọi số trận thắng là x và số trận hoà là y ( $x \in N *; y \in N *$ ).

Đội Arsenal đã thi đấu 38 trận mà không thua trận nào, nên ta có phương trình:

x + y = 38 (1)

Biết rằng với mỗi trận đấu, đội thắng được 3 điểm, đội thua không có điểm và nếu hai đội hoà nhau thì mỗi đội được 1 điểm mà đội Arsenal vô địch với 90 điểm nên ta có phương trình: 3x + y = 90 (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} x + y = 38 \\ 3 x + y = 90 \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 26 \\ y = 12 \end{matrix}$

Vậy đội Arsenal có số trận thắng là 26 trận.

Bài 12 trang 23 Toán 9 Tập 1: Nhân kỉ niệm ngày Quốc khánh 2/9, một nhà sách giảm giá mỗi cây bút bi là 20% và mỗi quyển vở là 10% so với giá niêm yết. Bạn Thanh vào nhà sách mua 20 quyển vở và 10 cây bút bi. Khi tính tiền, bạn Thanh đưa 175 000 đồng và được trả lại 3000 đồng. Tính giá niêm yết của mỗi quyển vở và mỗi cây bút bi, biết rằng tổng số tiền phải trả nếu không được giảm giá là 195 000 đồng.

Lời giải:

Gọi x và y lần lượt là giá niêm yết của mỗi quyển vở và mỗi cây bút bi (x;y > 0).

Tổng số tiền phải trả nếu không được giảm giá là 195 000 đồng, nên ta có phương trình: 20x + 10y = 195000 (1)

Giảm giá mỗi cây bút bi là 20% và mỗi quyển vở là 10% so với giá niêm yết và bạn Thanh đưa 175 000 đồng và được trả lại 3000 đồng, nên ta có phương trình:

(100% - 10%).20x + (100% - 20%).10y = 172000

hay 90%.20x + 80%.10y = 172000 (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} 20 x + 10 y = 195000 \\ 90 % .20 x + 80 % .10 y = 172000 \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 8 \\ y = 3, 5 \end{matrix}$

Vậy giá niêm yết của mỗi quyển vở là 8 nghìn đồng, giá niêm yết của mỗi cây bút bi là 3,5 nghìn đồng.

Bài 13 trang 23 Toán 9 Tập 1: Giải bài toán cổ sau:

Quýt, cam mười bảy quả tươi

Đem chia cho một trăm người cùng vui

Chia ba mỗi quả quýt rồi

Còn cam mỗi quả chia mười vừa xinh

Trăm người, trăm miếng ngọt lành

Quýt, cam mỗi loại tính rành là bao?

Lời giải:

Gọi x và y lần lượt là số quýt và số cam cần tìm (x;y > 0).

“Quýt, cam mười bảy quả tươi”, ta có phương trình: x + y = 17 (1)

“Đem chia cho một trăm người cùng vui

Chia ba mỗi quả quýt rồi

Còn cam mỗi quả chia mười vừa xinh”

Ta có phương trình: 10x + 3y = 100 (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} x + y = 17 \\ 10 x + 3 y = 100 \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 7 \\ y = 10 \end{matrix}$

Vậy số quýt là 10 quả, số cam là 7 quả.

Bài 14 trang 23 Toán 9 Tập 1: Trong một xí nghiệp, hai tổ công nhân A và B lắp ráp cùng một loại bộ linh kiện điện tử. Nếu tổ A lắp ráp trong 5 ngày, tổ B lắp ráp trong 4 ngày thì xong 1900 bộ linh kiện. Biết rằng mỗi ngày tổ A lắp ráp được nhiều hơn tổ B 20 bộ linh kiện. Hỏi trong một ngày mỗi tổ ráp được bao nhiêu bộ linh kiện điện tử? (Năng suất lắp ráp của mỗi tổ trong các ngày là như nhau).

Lời giải:

Gọi x và y lần lượt là số linh kiện mà tổ A và tổ B lắp ráp được trong một ngày (x;y > 0).

Nếu tổ A lắp ráp trong 5 ngày, tổ B lắp ráp trong 4 ngày thì xong 1900 bộ linh kiện, nên ta có phương trình: 5x + 4y = 1900 (1)

Biết rằng mỗi ngày tổ A lắp ráp được nhiều hơn tổ B 20 bộ linh kiện, ta có phương trình: x – y = 20 (2).

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} x - y = 20 \\ 5 x + 4 y = 1900 \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 220 \\ y = 200 \end{matrix}$

Vậy trong 1 ngày tổ A ráp được 220 bộ linh kiện, tổ B ráp được 200 bộ linh kiện.

Bài 15 trang 23 Toán 9 Tập 1: Cân bằng phương trình hoá học sau bằng phương pháp đại số.

a) Fe + Cl2 $\to$ FeCl3

b) SO2 + O2 $\to_{V_{2} O_{5}}^{t^{o}}$ SO3

c) Al + O2 $\to$ Al2O3

Lời giải:

a) Gọi x và y lần lượt là hệ số của Fe và Cl2 thoả mãn cân bằng phương trình hoá học

xFe + yCl2 $\to$ FeCl3

Cân bằng số nguyên tử Fe, số nguyên tử Cl ở 2 vế, ta có hệ phương trình:

${\begin{matrix} x = 1 \\ 2 y = 3 \end{matrix}$

Giải hệ phương trình, ta được: ${\begin{matrix} y = \frac{3}{2} \\ x = 1 \end{matrix}$

Đưa các hệ số tìm được vào phương trình hoá học, ta có

Fe + $\frac{3}{2}$ Cl2 $\to$ FeCl3

Do các hệ số của phương trình hoá học phải là các số nguyên nên nhân hai vế của phương trình hoá học với 2, ta được

2Fe + 3Cl2 $\to$ 2FeCl3

b) Gọi x và y lần lượt là hệ số của S và O2 thoả mãn cân bằng phương trình hoá học

xSO2 + yO2 $\to_{V_{2} O_{5}}^{t^{o}}$ SO3

Cân bằng số nguyên tử S, số nguyên tử O ở 2 vế, ta có hệ phương trình:

${\begin{matrix} x = 1 \\ 2 x + 2 y = 3 \end{matrix}$

Giải hệ phương trình, ta được: ${\begin{matrix} y = \frac{1}{2} \\ x = 1 \end{matrix}$

Đưa các hệ số tìm được vào phương trình hoá học, ta có

SO2 + $\frac{1}{2}$ O2 $\to_{V_{2} O_{5}}^{t^{o}}$ SO3

Do các hệ số của phương trình hoá học phải là các số nguyên nên nhân hai vế của phương trình hoá học với 2, ta được

2SO2 + O2 $\to_{V_{2} O_{5}}^{t^{o}}$ 2SO3

c) Gọi x và y lần lượt là hệ số của Al và O2 thoả mãn cân bằng phương trình hoá học

xAl + yO2 $\to$ Al2O3

Cân bằng số nguyên tử Al, số nguyên tử O ở 2 vế, ta có hệ phương trình:

${\begin{matrix} x = 2 \\ 2 y = 3 \end{matrix}$

Giải hệ phương trình, ta được: ${\begin{matrix} y = \frac{3}{2} \\ x = 2 \end{matrix}$

Đưa các hệ số tìm được vào phương trình hoá học, ta có

2Al + $\frac{3}{2}$ O2 $\to$ Al2O3

Do các hệ số của phương trình hoá học phải là các số nguyên nên nhân hai vế của phương trình hoá học với 2, ta được

4Al + 3O2 $\to$ 2Al2O3

Bài 16 trang 23 Toán 9 Tập 1: Nhà máy luyện thép hiện có sẵn loại thép chứa 10% carbon và loại thép chứa 20% carbon. Giả sử trong quá trình luyện thép các nguyên liệu không bị hao hụt. Tính khối lượng thép mỗi loại cần dùng để luyện được 1000 tấn thép chứa 16% carbon từ hai loại thép trên.

Lời giải:

Gọi x và y lần lượt là số tấn thép của loại 10% carbon và 20% carbon cần dùng (x;y > 0).

Cần dùng để luyện được 1000 tấn thép, tan có phương trình: x + y = 1000 (1)

cần dùng chứa 16% carbon từ hai loại thép trên, ta có phương trình:

10%x + 20%y = 1000.16% (2)

Từ (1) và (2) ta có hệ phương trình: ${\begin{matrix} x + y = 1000 \\ 10 % x + 20 % y = 1000.16 % \end{matrix}$

Giải hệ phương trình ta được: ${\begin{matrix} x = 400 \\ y = 600 \end{matrix}$

Vậy số tấn thép của loại 10% carbon cần dùng là 400 tấn và số tấn thép của loại 20% carbon cần dùng là 600 tấn.

Xem thêm các bài giải SGK Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 9

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương