Hoạt động 1 trang 26 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Mai Hương Ngày: 14-03-2024 Lớp 12

187

Với giải Hoạt động 1 trang 26 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Hoạt động 1 trang 26 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Hoạt động 1 trang 26 SGK Toán 12 Tập 1: Cho hàm số $y = x^{2} - 4 x + 3$ . Thực hiện lần lượt các yêu cầu sau:

a) Tính y’ và tìm các điểm tại đó $y^{'} = 0$ .

b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.

c) Tính $lim_{x \to - \infty} y$ , $lim_{x \to + \infty} y$ và lập bảng biến thiên của hàm số.

d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.

Lời giải:

a) Tập xác định: $D = R$

Ta có: $y^{'} = 2 x - 4, y^{'} = 0 \Leftrightarrow 2 x - 4 = 0 \Leftrightarrow x = 2$

Vậy với $x = 2$ thì $y^{'} = 0$ .

b) Trên khoảng $(- \infty; 2)$ , $y^{'} < 0$ nên hàm số nghịch biến. Trên khoảng $(2; + \infty)$ , $y^{'} > 0$ nên hàm số đồng biến.

Hàm số đạt cực tiểu tại $x = 2,$ giá trị cực tiểu $y_{C T} = - 1$ . Hàm số không có cực đại.

c) $lim_{x \to - \infty} y = lim_{x \to - \infty} (x^{2} - 4 x + 3) = lim_{x \to - \infty} [x^{2} (1 - \frac{4}{x} + \frac{3}{x^{2}})] = + \infty$

$lim_{x \to + \infty} y = lim_{x \to + \infty} (x^{2} - 4 x + 3) = lim_{x \to + \infty} [x^{2} (1 - \frac{4}{x} + \frac{3}{x^{2}})] = + \infty$

Bảng biến thiên: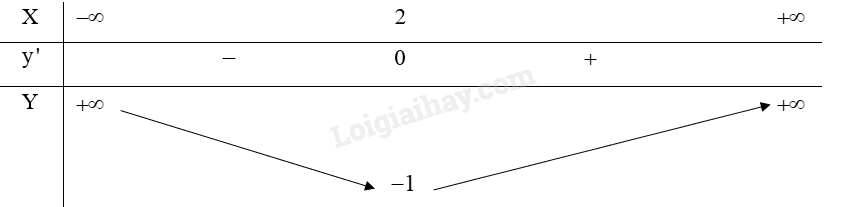

d) Đồ thị:

Giao điểm của đồ thị hàm số $y = x^{2} - 4 x + 3$ với trục tung là $(0; 3)$ .

Ta có: $x^{2} - 4 x + 3 = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$ . Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm $(3; 0); (1; 0)$ .

Điểm $(4; 3)$ thuộc đồ thị hàm số $y = x^{2} - 4 x + 3$ .

Đồ thị hàm số nhận đường thẳng $x = 2$ làm trục đối xứng.

d) Đồ thị:

Giao điểm của đồ thị hàm số $y = x^{2} - 4 x + 3$ với trục tung là $(0; 3)$ .

Ta có: $x^{2} - 4 x + 3 = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$ . Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm $(3; 0); (1; 0)$ .