Với Giải SBT Toán 10 Tập 1 trong Bài 2: Định lí côsin và định lí sin Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.
Cho tam giác MNP có M N = 10 , M P = 20 và ˆ M = 42 ∘
Bài 7 trang 75 SBT Toán 10: Cho tam giác MNP có MN=10,MP=20MN=10,MP=20 và ˆM=42∘
a) Tính diện tích tam giác MNP
b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP
Lời giải:
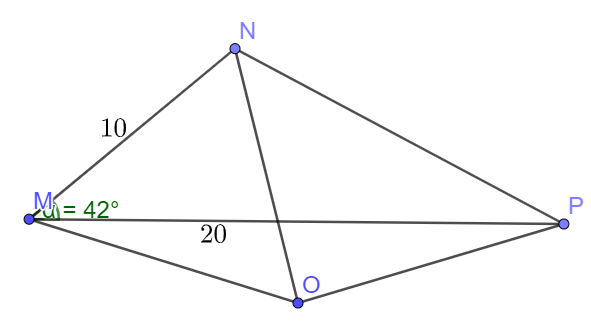
a) Ta có công thức S=12absinC=12.MN.MP.sinM
=12.10.20.sin42∘≃66,91 (đvdt)
b) O là tâm đường tròn ngoại tiếp tam giác MNP nên ta có:
OM=ON=OP=R=NP2sinM (*)
Áp dụng định lí côsin ta tính được NP như sau:
NP=√MP2+MN2−2.MP.MN.cosM≃14,24 (cm)
Thay NP vừa tính được vào (*) ta có:
OM=ON=OP=R=NP2sinM=14,242.sin42∘≃10,64
Tam giác ONP có ON=OP=10,64;NP=14,24
Áp dụng công thức Heron, ta có:
S=√p(p−a)(p−b)(p−c)≃56,3(cm2)
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo với cuộc sống hay, chi tiết khác:
Bài 1 trang 74 SBT Toán 10: Tính độ dài các cạnh chưa biết trong các tam giác sau:
Bài 2 trang 74 SBT Toán 10: Cho tam giác ABC , biết cạnh cm,
Bài 3 trang 75 SBT Toán 10: Tính góc lớn nhất của tam giác ABC, biết các cạnh là
Bài 4 trang 75 SBT Toán 10: Tính khoảng cách giữa hai điểm P và Q của một hồ nước (hình 7)
Bài 5 trang 75 SBT Toán 10: Cho tam giác ABC với . Chứng minh rằng:
Bài 6 trang 75 SBT Toán 10: Cho tam giác ABC có cm, cm, cm
Bài 9 trang 75 SBT Toán 10: Cho tam giác ABC và có các điểm B’, C’ trên các cạnh AB, AC
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.