Toán 10 Chân trời sáng tạo trang 78: Bài tập cuối chương 4

Giang Ngày: 08-02-2023 Lớp 10

332

Với giải Câu hỏi trang 78 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 4 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 78: Bài tập cuối chương 4

Bài 1 trang 78 Toán 10 Tập 1: Cho tam giác ABC. Biết $a = 49, 4; b = 26, 4; \hat{C} = 47^{\circ} 20^{'} .$ Tính hai góc $\hat{A}, \hat{B}$ và cạnh c.

Phương pháp giải

Bước 1: Tính cạnh c: Áp dụng định lí cosin: $c^{2} = b^{2} + a^{2} - 2 a b \cos C$

Bước 2: Tính hai góc $\hat{A}, \hat{B}$ : Áp dụng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lời giải

Áp dụng định lí cosin trong tam giác ABC, ta có: $\begin{array}{l} c^{2} = b^{2} + a^{2} - 2 a b \cos C \\ \Leftrightarrow c^{2} = 26, 4^{2} + 49, 4^{2} - 2.26, 4.49, 4 \cos 47^{\circ} 20^{'} \\ \Rightarrow c \approx 37 \end{array}$

Áp dụng định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

$\begin{array}{l} \Leftrightarrow \frac{49, 4}{\sin A} = \frac{26, 4}{\sin B} = \frac{37}{\sin 47^{\circ} 20^{'}} \\ \Rightarrow \sin A = \frac{49, 4. \sin 47^{\circ} 20^{'}}{37} \approx 0, 982 \Rightarrow \hat{A} \approx 79^{\circ} \\ \Rightarrow \hat{B} \approx 180^{\circ} - 79^{\circ} - 47^{\circ} 20^{'} = 53^{\circ} 40^{'} \end{array}$

Bài 2 trang 78 Toán 10 Tập 1: Cho tam giác ABC. Biết $a = 24, b = 13, c = 15.$ Tính các góc $\hat{A}, \hat{B}, \hat{C} .$

Phương pháp giải

Áp dụng hệ quả của định lí cosin:

Từ đó suy ra các góc $\hat{A}, \hat{B}, \hat{C} .$ $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Lời giải

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l} \cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \\ \Rightarrow \cos A = \frac{13^{2} + 15^{2} - 24^{2}}{2.13.15} = - \frac{7}{15}; \cos B = \frac{24^{2} + 15^{2} - 13^{2}}{2.24.15} = \frac{79}{90} \\ \Rightarrow \hat{A} \approx 117, 8^{\circ}, \hat{B} \approx 28, 6^{o} \\ \Rightarrow \hat{C} \approx 33, 6^{o} \end{array}$

Bài 3 trang 78 Toán 10 Tập 1: Cho tam giác ABC có $a = 8, b = 10, c = 13.$ Tính các góc $\hat{A}, \hat{B}, \hat{C} .$

Lời giải a

a) Tam giác ABC có góc tù không?

Phương pháp giải:

Áp dụng hệ quả của định lí cosin: $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

Từ đó suy ra các góc $\hat{A}, \hat{B}, \hat{C} .$

Lời giải

Áp dụng hệ quả của định lí cosin, ta có:

$\begin{array}{l} \cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c} \\ \Rightarrow {\begin{cases} \cos A = \frac{10^{2} + 13^{2} - 8^{2}}{2.10.13} = \frac{41}{52} > 0; \\ \cos B = \frac{8^{2} + 13^{2} - 10^{2}}{2.8.13} = \frac{133}{208} > 0 \\ \cos C = \frac{8^{2} + 10^{2} - 13^{2}}{2.8.13} = - \frac{1}{32} < 0 \end{cases} \end{array}$

$\Rightarrow \hat{C} \approx 91, 79^{\circ} > 90^{\circ}$ , tam giác ABC có góc C tù.

Lời giải b

b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.

Phương pháp giải:

+) Tính AM: Áp dụng định lí cosin trong tam giác ACM:

$A M^{2} = A C^{2} + C M^{2} - 2. A C . C M . \cos C$

+) Tính diện tích:

Áp dụng công thức heron: $S = \sqrt{p (p - a) (p - b) (p - c)}$

+) Tính R: Áp dụng định lí sin: $\frac{c}{\sin C} = 2 R \Rightarrow R = \frac{c}{2 \sin C}$

Lời giải

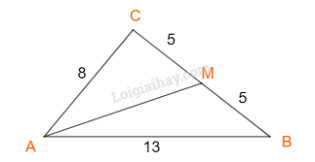
Bài 3 trang 78 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

+) Áp dụng định lí cosin trong tam giác ACM, ta có:

$\begin{array}{l} A M^{2} = A C^{2} + C M^{2} - 2. A C . C M . \cos C \\ \Leftrightarrow A M^{2} = 8^{2} + 5^{2} - 2.8.5. (- \frac{1}{32}) = 91, 5 \\ \Rightarrow A M \approx 9, 57 \end{array}$

+) Ta có: $p = \frac{8 + 10 + 13}{2} = 15, 5$ .

Áp dụng công thức heron, ta có: $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{15, 5. (15, 5 - 8) . (15, 5 - 10) . (15, 5 - 13)} \approx 40$

+) Áp dụng định lí sin, ta có:

$\frac{c}{\sin C} = 2 R \Rightarrow R = \frac{c}{2 \sin C} = \frac{13}{2. \sin 91, 79^{\circ}} \approx 6, 5$

Lời giải c

c) Lấy điểm D đối xứng với A qua C.

Phương pháp giải:

Áp dụng định lí cosin trong tam giác BCD:

$B D^{2} = C D^{2} + C B^{2} - 2. C D . C B . \cos \hat{B C D}$

Lời giải

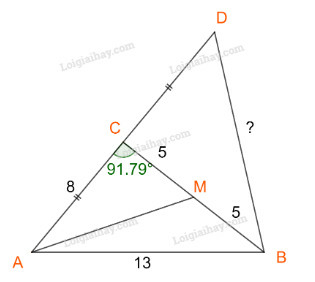
Bài 3 trang 78 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có: $\hat{B C D} = 180^{\circ} - 91, 79^{\circ} = 88, 21^{\circ}$ ; $C D = A C = 8$

Áp dụng định lí cosin trong tam giác BCD, ta có:

$\begin{array}{l} B D^{2} = C D^{2} + C B^{2} - 2. C D . C B . \cos \hat{B C D} \\ \Leftrightarrow B D^{2} = 8^{2} + 10^{2} - 2.8.10. \cos 88, 21^{\circ} \approx 159 \\ \Rightarrow B D \approx 12, 6 \end{array}$