Luyện tập 6 trang 37 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11

Luyện tập 6 trang 37 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11

Ngọc Nguyễn Ngày: 05-02-2024 Lớp 11

254

Với giải Luyện tập 6 trang 37 Toán 11 Tập 1 Cánh Diều chi tiết trong Bài 4: Phương trình lượng giác cơ bản giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Luyện tập 6 trang 37 Toán 11 Tập 1 | Cánh Diều Giải Toán lớp 11

Luyện tập 6 trang 37 Toán 11 Tập 1: Giải phương trình được nêu trong bài toán mở đầu.

Lời giải:

• Ta có:

550 + 450cos $\frac{π}{50}$ t = 1 000

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t = 450

$\Leftrightarrow$ cos $\frac{π}{50}$ t = 1

$\Leftrightarrow$ $\frac{π}{50}$ t = k2 $π$ (k $\in$ Z, t $\geq$ 0)

$\Leftrightarrow$ t = k2 $π$ . $\frac{50}{π}$ = 100k (k $\in$ Z, t $\geq$ 0).

Vậy phương trình này có các nghiệm là t = 100k với k ∈ ℤ, t ≥ 0.

• Ta có:

550 + 450cos $\frac{π}{50}$ t = 250

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t = -300

$\Leftrightarrow$ cos $\frac{π}{50}$ t = - $\frac{2}{3}$

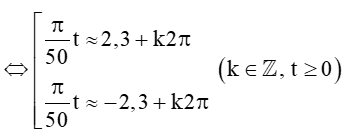
Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 12)

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 13) ta được kết quả gần đúng là 2,3)

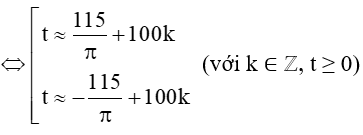
Toán 11 Bài 4 (Cánh diều): Phương trình lượng giác cơ bản (ảnh 14)

Vậy phương trình có các nghiệm là t $\approx \frac{115}{π}$ +100k và t $\approx - \frac{115}{π}$ +100k với k ∈ ℤ, t ≥ 0.

• Ta có:

550 + 450cos $\frac{π}{50}$ t = 100

$\Leftrightarrow$ 450cos $\frac{π}{50}$ t = -450

$\Leftrightarrow$ cos $\frac{π}{50}$ t = -1

$\Leftrightarrow$ $\frac{π}{50}$ t = $π$ + k2 $π$ (k $\in$ Z, t $\geq$ 0)

$\Leftrightarrow$ t = 50 + 100k (k $\in$ Z, t $\geq$ 0).

Vậy phương trình có các nghiệm là t = 50 + 100k với k ∈ ℤ, t ≥ 0.

Xem thêm các bài giải Toán 11 Cánh Diều hay, chi tiết khác:

Câu hỏi khởi động trang 32 Toán 11 Tập 1: Một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo là đường elip (Hình 32). Độ cao h (km) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h = 550 + 450cost (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021), trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Tại thời điểm t bằng bao nhiêu thì vệ tinh cách mặt đất 1 000 km; 250 km; 100 km?

Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x): x² ‒ 3x + 2 = 0 (1)

Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và $\frac{x^{2} - 1}{x + 1}$ =0 có tương đương không? Vì sao?

Hoạt động 2 trang 33 Toán 11 Tập 1: Khẳng định 3x ‒ 6 = 0 3x = 6 đúng hay sai?

Luyện tập 2 trang 33 Toán 11 Tập 1: Giải phương trình: (x – 1)² = 5x – 11.

Hoạt động 3 trang 33 Toán 11 Tập 1: a) Đường thẳng d: y = cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A₀, B₀ (Hình 33). Tìm hoành độ của hai giao điểm A₀, B₀.

Luyện tập 4 trang 35 Toán 11 Tập 1: Giải phương trình sin2x = sin $(x + \frac{π}{4})$ .

Hoạt động 4 trang 35 Toán 11 Tập 1: a) Đường thẳng d: y = cắt đồ thị hàm số y = cosx, x ∈ [‒π; π] tại hai giao điểm C₀, D₀ (Hình 34). Tìm hoành độ của hai giao điểm C₀, D₀.

Luyện tập 5 trang 36 Toán 11 Tập 1: a) Giải phương trình: cosx = -1/2

Luyện tập 6 trang 37 Toán 11 Tập 1: Giải phương trình được nêu trong bài toán mở đầu.

Hoạt động 5 trang 37 Toán 11 Tập 1: Quan sát các giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 (Hình 35).

Luyện tập 7 trang 37 Toán 11 Tập 1: a) Giải phương trình: tanx = 1.

Hoạt động 6 trang 38 Toán 11 Tập 1: Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 (Hình 36).

Luyện tập 8 trang 39 Toán 11 Tập 1: a) Giải phương trình: cotx = 1.

Luyện tập 9 trang 39 Toán 11 Tập 1: Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian (làm tròn kết quả đến hàng phần nghìn):

Bài 1 trang 40 Toán 11 Tập 1: Giải phương trình: a) sin $(2 x - \frac{π}{3}) = - \frac{\sqrt{3}}{2}$ ;

Bài 2 trang 40 Toán 11 Tập 1: Giải phương trình: a) sin $(2 x + \frac{π}{4})$ = sinx;

Bài 3 trang 40 Toán 11 Tập 1: Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:

Bài 4 trang 40 Toán 11 Tập 1: Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số d(t) = 3sin+12 với t ∈ ℤ và 0 < t ≤ 365.

Bài 5 trang 40 Toán 11 Tập 1: Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với t ≥ 0) bởi hệ thức h = |d| với d = 3cos, trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian t nào thì khoảng cách h là 3 m, 0 m?

Xem thêm các bài giải sách giáo khoa Toán 11 Cánh Dều hay, chi tiết khác:

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

291

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

312

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

340

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

288

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.