Bài 5.3 trang 109 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11

Bài 5.3 trang 109 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11

Ngọc Nguyễn Ngày: 03-02-2024 Lớp 11

475

Với giải Bài 5.3 trang 109 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 15: Giới hạn của dãy số giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Bài 5.3 trang 109 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11

Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi:

a) $u_{n} = \frac{n^{2} + 1}{2 n - 1}$ ;

b) $v_{n} = \sqrt{2 n^{2} + 1} - n$ .

Lời giải:

a) $u_{n} = \frac{n^{2} + 1}{2 n - 1}$

Chia cả tử và mẫu của u_n cho n², ta được $u_{n} = \frac{n^{2} + 1}{2 n - 1}$ $= \frac{1 + \frac{1}{n^{2}}}{\frac{2}{n} - \frac{1}{n^{2}}}$ .

Vì $\lim_{n \to + \infty} (1 + \frac{1}{n^{2}}) = 1 > 0$ , $\lim_{n \to + \infty} (\frac{2}{n} - \frac{1}{n^{2}}) = 0$ và $\frac{2}{n} - \frac{1}{n^{2}} > 0$ với mọi n nên

$\lim_{n \to + \infty} u_{n} = \lim_{n \to + \infty} \frac{n^{2} + 1}{2 n - 1} = + \infty$ .

b) $v_{n} = \sqrt{2 n^{2} + 1} - n$

Ta có: $\lim_{n \to + \infty} v_{n} = \lim_{n \to + \infty} (\sqrt{2 n^{2} + 1} - n)$ $= \lim_{n \to + \infty} (\sqrt{n^{2} (2 + \frac{1}{n^{2}})} - n)$

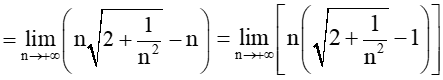
Toán 11 (Kết nối tri thức) Bài 15: Giới hạn của dãy số (ảnh 6)

Vì $\lim_{n \to + \infty} (\sqrt{2 + \frac{1}{n^{2}}} - 1) = \sqrt{2} - 1 > 0$ và $\lim_{n \to + \infty} n = + \infty$ .

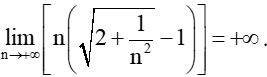
Nên Toán 11 (Kết nối tri thức) Bài 15: Giới hạn của dãy số (ảnh 7)

Vậy $\lim_{n \to + \infty} v_{n} = \lim_{n \to + \infty} (\sqrt{2 n^{2} + 1} - n) = + \infty$ .

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn là 0

Cho dãy số (u_n) với $u_{n} = \frac{{(- 1)}^{n}}{n}$ .

Luyện tập 1 trang 105 Toán 11 Tập 1: Chứng minh rằng $\lim_{n \to + \infty} \frac{{(- 1)}^{n - 1}}{3^{n}} = 0$ .

HĐ2 trang 105 Toán 11 Tập 1: Nhận biết dãy số có giới hạn hữu hạn Cho dãy số (u_n) với $u_{n} = \frac{n + {(- 1)}^{n}}{n}$ . Xét dãy số (v_n) xác định bởi v_n = u_n – 1.

Luyện tập 2 trang 106 Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{{3.2}^{n} - 1}{2^{n}}$ . Chứng minh rằng $\lim_{n \to + \infty} u_{n} = 3$ .

Vận dụng 1 trang 106 Toán 11 Tập 1: Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử u_n là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số (u_n) có giới hạn là 0.

HĐ3 trang 106 Toán 11 Tập 1: Hình thành quy tắc tính giới hạn

Cho hai dãy số (u_n) và (v_n) với $u_{n} = 2 + \frac{1}{n}, v_{n} = 3 - \frac{2}{n}$ .

Luyện tập 3 trang 107 Toán 11 Tập 1: Tìm $\lim_{n \to + \infty} \frac{\sqrt{2 n^{2} + 1}}{n + 1}$ .

HĐ4 trang 107 Toán 11 Tập 1: Làm quen với việc tính tổng vô hạn

Luyện tập 4 trang 108 Toán 11 Tập 1: Tính tổng $S = 2 + \frac{2}{7} + \frac{2}{49} + ... + \frac{2}{7^{n - 1}} + ...$

Vận dụng 2 trang 108 Toán 11 Tập 1: (Giải thích nghịch lí Zeno) Để đơn giản, ta giả sử Achilles chạy với vận tốc 100 km/h, vận tốc của rùa là 1 km/h và khoảng cách ban đầu là a = 100 (km).

HĐ5 trang 108 Toán 11 Tập 1: Nhận biết giới hạn vô cực. Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kì 4 giờ, số lượng của chúng sẽ tăng gấp đôi.

Luyện tập 5 trang 109 Toán 11 Tập 1: Tính $\lim_{n \to + \infty} (n - \sqrt{n})$ .

Bài 5.1 trang 109 Toán 11 Tập 1: Tìm các giới hạn sau: a) $\lim_{n \to + \infty} \frac{n^{2} + n + 1}{2 n^{2} + 1}$

Bài 5.2 trang 109 Toán 11 Tập 1: Cho hai dãy số không âm (u_n) và (v_n) với $\lim_{n \to + \infty} u_{n} = 2$ và $\lim_{n \to + \infty} v_{n} = 3$ . Tìm các giới hạn sau:

a) $\lim_{n \to + \infty} \frac{u_{n}^{2}}{v_{n} - u_{n}}$ ;

Bài 5.3 trang 109 Toán 11 Tập 1: Tìm giới hạn của các dãy số cho bởi: a) $u_{n} = \frac{n^{2} + 1}{2 n - 1}$ ;

Bài 5.4 trang 109 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số: a) 1,(12) = 1,121212...;

Bài 5.5 trang 109 Toán 11 Tập 1: Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng thuốc trong một thời gian dài.

Bài 5.6 trang 109 Toán 11 Tập 1: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA₁A₂A₃... Tính độ dài đường gấp khúc này theo h và α

Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

387

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

423

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

422

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

377

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.