a) Tính sđ $\stackrel{⏜}{ApB}$

b) Tính độ dài các cung $AqB$ và $ApB$

c) Tính diện tích hình quạt tròn $OAqB$

Phương pháp giải:

a) + Số đo góc ở tâm bằng số đo cung bị chắn

    + Số đo cung lớn bằng ${360}^{\circ }$$-$ số đo cung nhỏ.

b) Cho hình tròn bán kính $R$,  độ dài cung tròn $n^{\circ }$ là $l={\displaystyle \frac{\pi Rn}{180}}$

    Chu vi hình tròn đó là $C=2\pi R$

c) Cho hình tròn bán kính $R$,  diện tích quạt tròn số đo $n^{\circ }$ là $S={\displaystyle \frac{\pi R^{2}n}{360}}$

Trả lời:

a) Từ giả thiết $\widehat{AOB}={75}^{\circ }$  $\Rightarrow$ sđ$\stackrel{⏜}{AqB}$$={360}^{\circ }-$ sđ$\stackrel{⏜}{AB}$

Vậy  sđ$\stackrel{⏜}{ApB}$$={360}^{\circ }-{75}^{\circ }={285}^{\circ }$ 

b) Gọi $l_{\stackrel{⏜}{AqB}},l_{\stackrel{⏜}{ApB}}$ lần lượt là độ dài của các cung $AqB,ApB;C=2\pi R$ là độ dài đường tròn tâm $O.$

Theo công thức tính độ dài cung ta có : 

${\displaystyle l_{\stackrel{⏜}{AqB}}}$ $={\displaystyle \frac{\pi Rn}{180}=\frac{\pi .2.75}{180}=\frac{5}{6}\pi (cm)}$ 

Vậy  $l_{\stackrel{⏜}{ApB}}=C-l_{\stackrel{⏜}{AqB}}=4\pi -{\displaystyle \frac{5\pi }{6}}$$={\displaystyle \frac{19\pi }{6}}\left(cm\right).$

c) Ta có $\widehat{AOB}$ $={75}^{\circ };R=2cm$

Vậy $S_{OAqB}={\displaystyle \frac{\pi {.2}^2.75}{360}}={\displaystyle \frac{5\pi }{6}}\left(c{m}^2\right).$

a) Có phải ${\displaystyle \frac{1}{2}}$ số học sinh là học sinh ngoại trú không ?

b) Có phải ${\displaystyle \frac{1}{3}}$ số học sinh là học sinh bán trú không ?

c) Số học sinh nội trú chiếm bao nhiêu phần trăm ?

d) Tính số học sinh mỗi loại, biết tổng số học sinh là $1800$ em.

Phương pháp giải:

Tính số đo các cung, sau đó tính tỉ lệ.

Trả lời:

Biểu đồ hình quạt có tổng số đo ba góc ở tâm là ${180}^{\circ }$ mà theo hình 63 ta có hình quạt biểu diễn học sinh ngoại trú có số đo góc ở tâm là ${90}^{\circ },$ bán trú có số đo góc ở tâm là ${60}^{\circ }$ và nội  trú có số đo góc ở tâm là ${30}^{\circ }.$

Vậy:

a)  ${\displaystyle \frac{1}{2}}$ số học sinh là học sinh ngoại trú.

b) ${\displaystyle \frac{1}{3}}$ số học sinh là học sinh bán trú.

c) Số học sinh nội trú là ${\displaystyle \frac{1}{6}}$ tổng số học sinh, chiếm  $16,7\mathrm{\%}$ .

d) Số học sinh ngoại trú là ${\displaystyle \frac{1}{2}}$ tổng số học sinh bằng $900$  em.

     Số học sinh bán trú là  ${\displaystyle \frac{1}{3}}$ tổng số học sinh bằng $600$  em.

      Số học sinh nội trú là  ${\displaystyle \frac{1}{6}}$ tổng số học sinh bằng $300$  em.

Các đường cao hạ từ $A$ và $B$ của tam giác $ABC$ cắt nhau tại $H$ (góc $C$ khác $90$^o) và cắt đường tròn ngoại tiếp tam giác $ABC$ lần lượt tại $D$ và $E$. Chứng minh rắng:

a) $CD=CE$

b) Tam giác $BHD$ cân

c) $CD=CH$

Phương pháp giải:

a)  Sử dụng: “Số đo góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn” từ đó suy ra hai cung bằng nhau và hai dây bằng nhau.

b)  Chứng minh tam giác $HBD$ có $BM$ vừa là đường cao vừa là đường phân giác nên nó là tam giác cân

c)  Sử dụng tính chất đường trung trực của đoạn thẳng $HD.$

Trả lời:

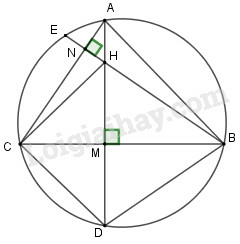
a) Gọi $M,N$ lần lượt là giao điểm của $AD$ với $BC$ và $BE$ với $AC.$

Các góc $ANB$ và $AMB$ là hai  góc có đỉnh nằm bên trong đường tròn nên  ta có :

$\widehat{ANB}={\displaystyle \frac{1}{2}}$(sđ $\stackrel{⏜}{EC}+$ sđ $\stackrel{⏜}{AB}$) $={90}^{\circ }$ (vì $BE\mathrm{\perp }AC$)

$\widehat{AMB}={\displaystyle \frac{1}{2}}$ (sđ$\stackrel{⏜}{DC}+$ sđ $\stackrel{⏜}{AB}$) $={90}^{\circ }$ (vì $AD\mathrm{\perp }BC$)

Vậy ta có  sđ$\stackrel{⏜}{CE}=$ sđ$\stackrel{⏜}{CD}$$\iff CD=CE$

b) Các góc $EBC$ và $CBD$ là hai  góc nội tiếp nên  ta có :

$\widehat{EBC}={\displaystyle \frac{1}{2}}$ sđ$\stackrel{⏜}{EC}$ và $\widehat{CBD}={\displaystyle \frac{1}{2}}$ sđ$\stackrel{⏜}{DC}$

Theo câu a) ta có $\stackrel{⏜}{CD}=\stackrel{⏜}{CE}$, suy ra $\widehat{EBC}=\widehat{CBD}.$

Do đó,  $BM$ vừa là đường cao vừa là đường phân giác của  $\mathrm{\Delta }BHD$.

Vậy $\mathrm{\Delta }BHD$ cân .

c) Vì $\mathrm{\Delta }BHD$ cân nên $BM$ là đường trung trực của đoạn $HD\Rightarrow MH=MD.$

Xét $\mathrm{\Delta }HMC$ và $\mathrm{\Delta }DMC$ vuông tại $M$ và $CM$ là cạnh chung; $MH=MD.$

Vậy $\mathrm{\Delta }HMC=\mathrm{\Delta }DMC$ $\Rightarrow CD=CH.$ 

Bài 58 trang 126 Vở bài tập toán 9 tập 2

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và tia phân giác của góc $A$ cắt đường tròn tại $M$. Vẽ đường cao $AH$. Chứng minh rằng:

a) $OM$ đi qua trung điểm của dây $BC$

b) $AM$ là tia phân giác của góc $OAH$ 

Phương pháp giải:

+ Sử dụng : “ Đường kính đi qua điểm chính giữa một cung thì vuông góc và đi qua trung điểm của dây căng cung đó”

+ Sử dụng tính chất hai đường thẳng song song và tính chất tam giác cân. 

Trả lời:

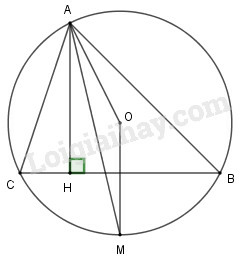
a) $AM$ là tia phân giác góc $A$ $\Rightarrow \widehat{BAM}=\widehat{CAM}$

Vì $\widehat{BAM}$ và $\widehat{MAC}$ là hai góc nội tiếp $\Rightarrow \stackrel{⏜}{BM}=\stackrel{⏜}{MC}$ hay $M$ là điểm chính giữa của cung $BC.$ 

Theo định lý về đường kính đi qua điểm chính giữa của một cung ta có $OM\mathrm{\perp }BC$ và $OM$ đi qua trung điểm dây $BC$.

b) Theo câu a)  ta có $OM\mathrm{\perp }BC$

Theo giả thiết $AH\mathrm{\perp }BC$

Vậy $AH//OM$

Do đó, $\widehat{OMA}=\widehat{MAH}$  (so le trong) .

Mặt khác, $\mathrm{\Delta }AOM$ cân vì $OM=OA$.

Do đó, ta có $\widehat{MAO}=\widehat{AMO}$

hay $AM$ là tia  phân giác của  góc $OAH.$

Cho tam giác $ABC$ vuông ở $A$. Trên $AC$ lấy một điểm $D$ và vẽ đường tròn đường kính $MC$. Kẻ $BM$ cắt đường tròn tại $D$. Đường thẳng $DA$ cắt đường tròn tại $S$. Chứng minh rằng:

a) $ABCD$ là tứ giác nội tiếp

b) $\widehat{ABD}=\widehat{ACD}$

c) $CA$ là tia phân giác của góc $SCB$ 

Phương pháp giải:

+ Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Nếu hai đỉnh kề một cạnh của một tứ giác cùng nhìn cạnh đối diện dưới các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp.

+ Sử dụng: “Hai góc nội tiếp cùng chắn một cung thì bằng nhau”

Trả lời:

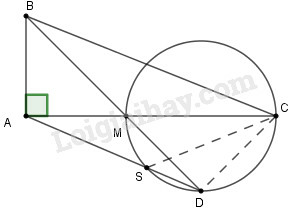
a) Theo giả thiết ta có :

$\widehat{BAC}={90}^{\circ }$

$\widehat{MDC}={90}^{\circ }$ (góc nội tiếp chắn nửa đường tròn đường kính $MC$)

Hai điểm $A$ và $D$ cùng nhìn đoạn thẳng $BC$ cố định dưới góc ${90}^{\circ }$ nên $A$ và $D$ thuộc đường tròn đường kính $BC$.

Vậy $ABCD$ là tứ giác nội tiếp đường tròn đường kính $BC.$

b) Vì $ABCD$ nội tiếp đường tròn đường kính $BC$ nên ta có:

 $\widehat{ABD}=\widehat{ACD}$  (cùng chắn cung $AD$).

c) Trong đường tròn đường kính $MC$ ta có:

 $\widehat{MCS}=\widehat{MDS}$ (vì cùng chắn cung $MS$)                 (1)

Xét đường tròn đường kính $BC$ ta có:

  $\widehat{BCA}=\widehat{BDA}$ (vì cùng chắn cung $BA$)                 (2)

Từ (1) và (2) ta có  $\widehat{BCA}=\widehat{ACS}.$

Vậy  tia $CA$ là tia phân giác của góc $SCB.$

Cho đường tròn $(O)$ và một điểm $A$ cố định trên đường tròn. Tìm quỹ tích các trung điểm $M$ của dây $AB$ khi điểm $B$ di động trên đường tròn đó.

Phương pháp giải:

+ Phần thuận: Lập luận để có $\widehat{AMO}={90}^{\circ }$ suy ra quỹ tích điểm $M$ là đường tròn đường kính $AO.$

+ Chứng minh phần đảo và kết luận.

Trả lời:

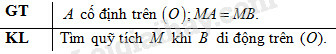
Phần thuận:

Kẻ đường kính $AC;$ kẻ dây $AB$; nối $MO.$ Các điểm $A$ và $O$ cố định. Khi đó, ta có : $MA=MB$ và $MO\mathrm{\perp }AB$ vì đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc dây đó.

$\Rightarrow \widehat{AMO}={90}^{\circ }.$

Khi $B$ thay đổi trên cung $AC$ thì  $M$ luôn nhìn cạnh $AO$ cố định dưới một góc bằng ${90}^{\circ }$ nên điểm $M$ thuộc  đường tròn đường kính $AO.$

Phần đảo:

Lấy điểm $M^{\prime }$ bất kì khác $O$ và $A$ thuộc đường tròn đường kính $AO$. Tia $A{M}^{\prime }$ cắt đường tròn đường kính $AC$  tại $B^{\prime }$. Kẻ $O{M}^{\prime }$. Ta phải chứng minh $M^{\prime }A=M^{\prime }{B}^{\prime }$.

Thật vậy $\widehat{A{M}^{\prime }O}={90}^{\circ }$ (vì góc nội tiếp chắn nửa đường tròn)

$\Rightarrow O{M}^{\prime }\mathrm{\perp }A{B}^{\prime }$ nên $M^{\prime }$ là trung điểm đoạn $A{B}^{\prime }$ ( vì đường kính vuông góc với dây thì đi qua trung điểm dây đó)

Suy ra $A{M}^{\prime }=M^{\prime }{B}^{\prime }$.

Kết luận:

Quỹ tích các điểm $M$ khi $B$ di động trên đường tròn $\left(O\right)$ là đường tròn đường kính $AO.$