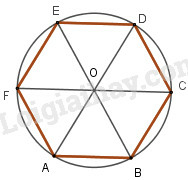
Vì các cạnh của lục giác đều bằng nhau nên ta có 6 cung bằng nhau và số đo mỗi cung bằng ${\displaystyle \frac{{360}^{\circ }}{6}}={60}^{\circ }.$

Khi đó, độ dài cung nhỏ $AB$ là $l_{AB}={\displaystyle \frac{\pi R.60}{180}}={\displaystyle \frac{\pi R}{3}}$

Lại có $\widehat{AOB}={60}^{\circ }$ (=sđ$\stackrel{⏜}{AB}$)

mà tam giác $OAB$ cân tại $O$ (do $OA=OB$) suy ra $OAB$ là tam giác đều

Từ đó $AB=OA=R.$

Tỉ số cần tìm là $AB:l_{AB}=R:{\displaystyle \frac{\pi R}{3}}=3:\pi$.

Chọn C.

Câu 22

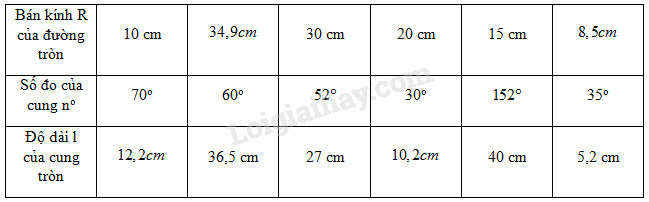
Lấy giá trị gần đúng của  bằng 3,14. Hãy điền vào ô trống (…) trong bảng sau (làm tròn đến chữ số thập phân thứ nhất và đến độ):

Phương pháp giải:

Sử dụng công thức tính độ dài cung $l={\displaystyle \frac{\pi Rn}{180}}$  với $n^{\circ }$ là số đo cung và $R$ là bán kính đường tròn.

Từ đó suy ra $n={\displaystyle \frac{180l}{\pi R}};R={\displaystyle \frac{180l}{\pi n}}$ .

Trả lời:

+ $R=10cm;n=70\Rightarrow l={\displaystyle \frac{\pi Rn}{180}}$$={\displaystyle \frac{3,\mathrm{14.10.70}}{180}}\approx 12,2cm$

+ $n=60;l=36,5\Rightarrow R={\displaystyle \frac{180l}{\pi n}}$$={\displaystyle \frac{180.36,5}{3,14.60}}\approx 34,9cm$

+ $R=30cm;l=27cm\Rightarrow n={\displaystyle \frac{180l}{\pi R}}$$={\displaystyle \frac{180.27}{3,14.30}}\approx 52$

+ $R=20cm;n=30\Rightarrow l={\displaystyle \frac{\pi Rn}{180}}$$={\displaystyle \frac{3,\mathrm{14.20.30}}{180}}\approx 10,5cm$

+ $R=15cm;l=40cm\Rightarrow n={\displaystyle \frac{180l}{\pi R}}$$={\displaystyle \frac{180.40}{3,14.15}}\approx 152$

+ $n=35;l=5,2cm\Rightarrow R={\displaystyle \frac{180l}{\pi n}}$$={\displaystyle \frac{180.5,2}{3,14.35}}\approx 8,5cm$

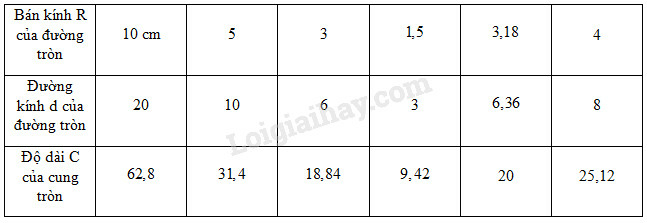
Lấy giá trị gần đúng của  bằng 3,14. Hãy điền vào ô trống (…) trong bảng sau (đơn vị độ dài: cm, làm tròn đến chữ số thập phân thứ nhất và đến độ):

Phương pháp giải:

Sử dụng các công thức:

Chu vi đường tròn có bán kính $R$ là $C=2\pi R=\pi d$ với $d=2R$ là đường kính của đường tròn.

Suy ra $R={\displaystyle \frac{C}{2\pi }};R={\displaystyle \frac{d}{2}};d={\displaystyle \frac{C}{\pi }}.$ 

Trả lời:

Từ công thức tính độ dài  đường tròn $C=2\pi R$ hay $C=\pi d(d=2R)$ ta có :

a) Khi $R=10\Rightarrow C=2\pi .10$$=2.3,14.10=62,8;$$d=2R=20\left(cm\right).$

b) Khi $d=10\Rightarrow R=5cm;$$C=3,14.10=31,4\left(cm\right).$

c) Khi $C=20\Rightarrow d={\displaystyle \frac{20}{\pi }}$ và $R={\displaystyle \frac{10}{\pi }}\approx 3,18.$  

Các trường hợp khác tính tương tự và điền kết quả vào bảng trên.

a) Tính độ dài cung ${60}^{\circ }$  của một đường tròn có bán kính $3dm$.

b) Tính chu vi vành xe đạp có đường kính $650mm$.

Phương pháp giải:

a) Sử dụng công thức tính độ dài cung $l={\displaystyle \frac{\pi Rn}{180}}$  với $n^{\circ }$ là số đo cung và $R$ là bán kính đường tròn.

b) Chu vi đường tròn có bán kính $R$ là $C=2\pi R=\pi d$ với $d=2R$ là đường kính của đường tròn.

Trả lời:

a) Theo công thức $l={\displaystyle \frac{\pi Rn}{180}},$ ta có $n^{\circ }={60}^{\circ },R=2dm=20cm.$

Vậy $l={\displaystyle \frac{\pi Rn}{180}}={\displaystyle \frac{\pi .20.60}{180}}={\displaystyle \frac{20\pi }{3}}$ (cm)

b) Từ công thức $C=\pi d,$ ta có $d=650mm=65cm$.

Vậy $C=\pi d=65\pi \left(cm\right).$

Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$. Chứng minh rằng độ dài của nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$.

Phương pháp giải:

Nửa đường tròn có bán kính $R$ có độ dài  là $l=\pi R={\displaystyle \frac{\pi d}{2}}$ với $d=2R$ là đường kính của đường tròn. 

Trả lời:

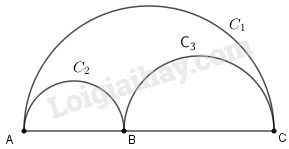
Gọi $C_1;C_2;C_3$ lần lượt là độ dài của các nửa đường tròn đường kính $AC,AB,BC.$ Theo công thức $C=\pi d$ ta có :

$C_1={\displaystyle \frac{1}{2}}\pi AC$ (vì $C_1$ là nửa đường tròn đường kính $AC$)

$C_2={\displaystyle \frac{1}{2}}\pi AB$ (vì $C_2$ là nửa đường tròn đường kính $AC$)

$C_3={\displaystyle \frac{1}{2}}\pi BC$ (vì $C_3$ là nửa đường tròn đường kính $AC$)

Từ đó ta có $C_2+C_3={\displaystyle \frac{1}{2}}\pi AB+{\displaystyle \frac{1}{2}}\pi BC$$={\displaystyle \frac{1}{2}}\pi \left(AB+BC\right)$

Vì $B$ nằm giữa $A$ và $C$$\Rightarrow AC=AB+BC.$

Vậy $C_1=C_2+C_3$

Chú ý: Vì $C_1;C_2;C_3$ lần lượt là độ dài của các nửa đường tròn đường kính $AC,AB,BC.$ Nên ta phải có ${\displaystyle \frac{1}{2}}$ ở công thức tính nửa chu vi là $C_1={\displaystyle \frac{1}{2}}\pi AC.$

Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe có đường kính là $1,672m$ và bánh xe trước có đường kính là $88cm$. Hỏi khi bánh xe sau lăn được $10$ vòng thì bánh xe trước lăn được mấy vòng ?

Phương pháp giải:

+ Tính chu vi các bánh xe theo công thức: Chu vi đường tròn có bán kính $R$ là $C=2\pi R=\pi d$ với $d=2R$ là đường kính của đường tròn.

+ Tính quãng đường ứng với bánh xe sau lăn được $10$ vòng, từ đó tính số vòng bánh xe trước lăn được.

Trả lời:

 Ta gọi $d_1=88cm=0,88m;$ $d_2=1,672m$ và $C_1;C_2$ lần lượt là độ dài của bánh xe trước và bánh xe sau.

Theo công thức $C=\pi d$ ta có : $C_1=0,88\pi \left(m\right),$$C_2=1,672\pi \left(m\right).$

Bánh xe sau lăn được 10 vòng tương ứng với quãng đường là :

                 $C_2.10=16,72\pi \left(m\right).$

Vậy số vòng bánh  xe trước lăn được là: ${\displaystyle \frac{C_2.10}{C_1}}=19$ ( vòng)

Bài 45 trang 118 Vở bài tập toán 9 tập 2

Bánh xe của một ròng rọc có chu vi $540mm$. Dây cu roa bao bánh xe theo cung AB có độ dài $200mm$. Tính góc $AOB$ (h.56)

Phương pháp giải:

+)  Sử dụng công thức tính  chu vi đường tròn có bán kính $R$ là $C=2\pi R\Rightarrow R={\displaystyle \frac{C}{2\pi }}$

 +) Sử dụng công thức tính độ dài cung $l={\displaystyle \frac{\pi Rn}{180}}$  với $n^{\circ }$ là số đo cung và $R$ là bán kính đường tròn.

Từ đó suy ra số đo cung $AB$ và góc $AOB.$

Trả lời:

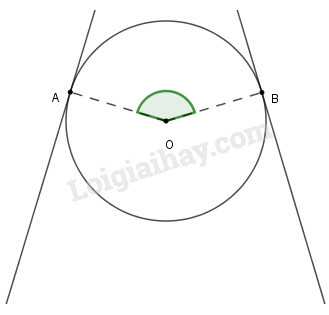
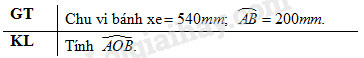
Theo công thức tính độ dài cung tròn ta có:

$l={\displaystyle \frac{\pi Rn}{180}}\Rightarrow n={\displaystyle \frac{180.l}{\pi R}}(1)$

Theo công thức tính độ dài đường tròn ta có :

$C=2\pi R,$ mà $C=540mm$

Do đó , ta có  $\pi R=270\left(2\right).$

Thay (2) vào (1) , ta được  : $n={\displaystyle \frac{200.180}{\pi .R}}={\displaystyle \frac{400}{3}}\approx 133$

Góc $AOB$ là góc ở tâm chắn cung $AB$. Vậy $\widehat{AOB}=n^{\circ }\approx {133}^{\circ }.$

Vĩ độ của Hà Nội là ${20}^{\circ }{01}^{\prime }$. Mỗi vòng kinh tuyến Trái Đất khoảng $40000km$. Tính độ dài cung kinh tuyến từ Hà Nội đến xích đạo.

Phương pháp giải:

+)  Sử dụng công thức tính  chu vi đường tròn có bán kính $R$ là $C=2\pi R\Rightarrow R={\displaystyle \frac{C}{2\pi }}$

 +) Sử dụng công thức tính độ dài cung $l={\displaystyle \frac{\pi Rn}{180}}$  với $n^{\circ }$ là số đo cung và $R$ là bán kính đường tròn.

Trả lời:

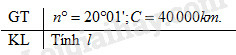
Từ giả thiết suy ra :

$n^{\circ }={\left(20+{\displaystyle \frac{1}{60}}\right)}^o={\left({\displaystyle \frac{1201}{60}}\right)}^o.$

Theo công thức tính độ dài cung ta có : $l={\displaystyle \frac{\pi Rn}{180}}$ (1)

Vì $C=2\pi R\Rightarrow 2\pi R=40000$. Thay $\pi R=20000$ vào (1), ta được :

$l={\displaystyle \frac{\pi Rn}{180}}={\displaystyle \frac{20000.{\displaystyle \frac{1201}{60}}}{180}}$$\approx 2224,07km$

Cho đường tròn $(O)$, bán kính $OM$. Vẽ đường tròn tâm $O^{\prime }$, đường kính $OM$. Một bán kính $OA$ của đường tròn $(O)$ cắt đường tròn $(O^{\prime })$ tại $B$. Chứng minh cung $MA$ và cung $MB$ có độ dài bằng nhau.

Phương pháp giải:

+ Sử dụng tính chất: “Số đo góc nội tiếp bằng nửa số đo cung bị chắn” và “số đo góc ở tâm bằng số đo cung bị chắn.”

+ Sử dụng công thức tính độ dài cung $l={\displaystyle \frac{\pi Rn}{180}}$  với $n^{\circ }$ là số đo cung và $R$ là bán kính đường tròn.

Trả lời:

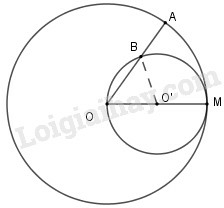
Giả sử $\widehat{MOA}=n^{\circ }$.

Ta có  $\widehat{M{O}^{\prime }B}$ =sđ$\stackrel{⏜}{MB}$ và $\widehat{MOB}={\displaystyle \frac{1}{2}}$ sđ$\stackrel{⏜}{MB}$  (1)  (vì  góc ở tâm và góc nội tiếp chắn cung $MB$)

Mà $\widehat{MOB}=\widehat{MOA}=$ sđ$\stackrel{⏜}{AM}$     (2)

Từ (1) và (2) ta có : sđ$\stackrel{⏜}{MB}$ = 2 . sđ $\stackrel{⏜}{AM}$$=2n^{\circ }.$

Theo công thức tính độ dài cung ta có  $l_{MA}={\displaystyle \frac{\pi .OM.n}{180}}$  và $l_{MB}={\displaystyle \frac{\pi .O^{\prime }M.2n}{180}}={\displaystyle \frac{\pi .2O^{\prime }M.n}{180}}$

Theo giả thiết $OM=2O^{\prime }M.$ Vậy các  cung $MA$ và $MB$ có độ dài bằng nhau.