Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 8. Đường tròn ngoại tiếp - Đường tròn nội tiếp trang 113,114,115 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 8. Đường tròn ngoại tiếp - Đường tròn nội tiếp

 Phần câu hỏi bài 8 trang 113 Vở bài tập toán 9 tập 2

Câu 19

Cho một đường tròn bán kính r nội tiếp trong tam giác vuông cân và một đường tròn bán kính R ngoại tiếp tam giác ấy. Khi đó tỉ số ${\displaystyle \frac{R}{r}}$ bằng:

(A) $1+\sqrt{2}$                    (B) $2+\sqrt{2}$

(C) $\sqrt{2}-1$                     (D) $\sqrt{2}-2$

Phương pháp giải:

+ Xác định tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền và suy ra bán kính $R.$

Xác định tâm đường tròn nội tiếp tam giác là giao ba đường phân giác và suy ra bán kính $r.$

+ Sử dụng định lý Pytago và tính chất đường phân giác trong tam giác để biến đổi.

Trả lời:

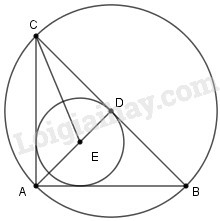
Xét tam giác $ABC$ vuông cân tại $A.$ Gọi $D$ là trung điểm $BC$ và $E$ là giao điểm đường phân giác $\widehat{ACB}$ và $AD.$

Khi đó $DA=DB=DC\left(={\displaystyle \frac{1}{2}}BC\right)$  nên $D$ là tâm đường tròn ngoại tiếp tam giác $ABC$ và bán kính của nó là $R=AD$

Vì $ABC$ cân tại $A$ nên $AD$ vừa là đường trung tuyến vừa là đường phân giác nên $E$ là tâm đường tròn nội tiếp tam giác $ABC$ và bán kính của nó là $r=DE.$

Xét tam giác $CAD$ có $CE$ là phân giác góc $ACD$ nên ${\displaystyle \frac{ED}{EA}}={\displaystyle \frac{DC}{AC}}$ (tính chất đường phân giác)

Suy ra ${\displaystyle \frac{ED}{ED+EA}}={\displaystyle \frac{DC}{DC+CA}}$$\iff {\displaystyle \frac{ED}{AD}}={\displaystyle \frac{DC}{DC+CA}}$$\iff {\displaystyle \frac{r}{R}}={\displaystyle \frac{DC}{DC+CA}}$ (1)

Xét tam giác $ABC$, theo định lý Pytago ta có $BC=\sqrt{A{B}^2+A{C}^2}$$=\sqrt{A{C}^2+A{C}^2}=\sqrt{2A{C}^2}$$=AC\sqrt{2}$  (vì $AB=AC)$ nên $DC={\displaystyle \frac{BC}{2}}={\displaystyle \frac{AC\sqrt{2}}{2}}$  suy ra ${\displaystyle \frac{DC}{DC+CA}}={\displaystyle \frac{{\displaystyle \frac{AC\sqrt{2}}{2}}}{{\displaystyle \frac{AC\sqrt{2}}{2}}+AC}}$$={\displaystyle \frac{{\displaystyle \frac{AC\sqrt{2}}{2}}}{{\displaystyle \frac{AC\sqrt{2}+2AC}{2}}}}={\displaystyle \frac{{\displaystyle \frac{\sqrt{2}}{2}}}{{\displaystyle \frac{\sqrt{2}+2}{2}}}}$$={\displaystyle \frac{\sqrt{2}}{2+\sqrt{2}}}={\displaystyle \frac{1}{\sqrt{2}+1}}$ (2)

Từ (1) và (2) suy ra ${\displaystyle \frac{r}{R}}={\displaystyle \frac{1}{\sqrt{2}+1}}\iff {\displaystyle \frac{R}{r}}=\sqrt{2}+1$

Chọn A.

Câu 20

Chọn từ thích hợp điền vào chỗ trống trong câu sau:

Trong đa giác đều, tâm…..trùng với tâm……..và được gọi là tâm……

Phương pháp giải:

Ta sử dụng: Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

Trả lời:

Trong đa giác đều, tâm đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp và được gọi là tâm đa giác đều.

a) Vẽ đường tròn tâm O, bán kính 2 cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O ; r).

Phương pháp giải:

+ Xác định tâm và bán kính của đường tròn sau đó vẽ đường tròn

+ Sử dụng hệ thức lượng trong tam giác vuông để tính toán.

Trả lời:

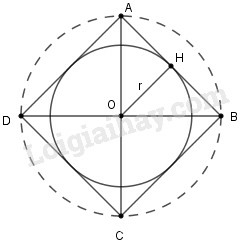
a)  Lấy điểm $O$ làm tâm, vẽ đường tròn có tâm $O$ và bán kính $R=2cm.$

b) Kẻ hai đường kính $AC$ và $BD$ vuông góc với nhau. Nối $AB,BC,CD,DA$ ta được hình vuông $ABCD$ nội tiếp đường tròn $\left(O\right).$

c) Kẻ $OH\mathrm{\perp }AB$. $OH$ là bán kính $r$ của đường tròn nội tiếp hình vuông $ABCD.$

Xét $\mathrm{\Delta }AOB$ là tam giác vuông cân tại $O$ và $OH\mathrm{\perp }AB$ nên $OH$ là vừa là đường cao vừa là đường trung tuyến của $\mathrm{\Delta }AOB.$

Suy ra $OH=HA=HB\left(1\right)$. Do đó,  $O{A}^2=O{H}^2+A{H}^2,$ hay $O{A}^2=2.r^2.$

Mà $OA=2\Rightarrow r=\sqrt{2}.$

Vẽ đường tròn $\left(O;r\right)$ là đường tròn nội tiếp hình vuông $ABCD$ vì tiếp xúc với bốn cạnh của hình vuông.

a) Vẽ tam giác đều $ABC$ cạnh $a=3cm$

b) Vẽ tiếp đường tròn $(O;R)$ ngoại tiếp tam giác đều $ABC$. Tính $R$

c) Vẽ tiếp đường tròn $(O;r)$ nội tiếp tam giác đều $ABC$. Tính $r$

d) Vẽ tiếp tam giác đều $IJK$ ngoại tiếp đường tròn $(O;R)$.

Phương pháp giải:

Sử dụng: Tâm tam giác đều vừa là tâm đường tròn ngoại tiếp và vừa là tâm đường tròn nội tiếp.

Tính bán kính dựa vào định lý Pytago và tính chất trọng tâm tam giác.

Trả lời:

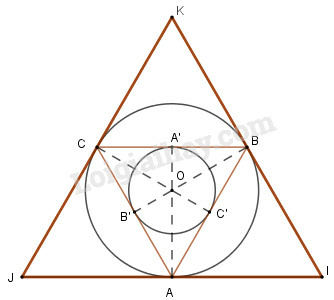
a) Vẽ tam giác đều $ABC$,  cạnh $a=3cm$ bằng thước và compa.

b) Vẽ đường tròn $\left(O;R\right)$ ngoại tiếp $\mathrm{\Delta }ABC$ :

-  Gọi $O$ là giao điểm của ba đường trung trực $A{A}^{\prime },B{B}^{\prime },C{C}^{\prime }$ của tam giác đều$ABC$ nên $O$ là tâm của  đường tròn ngoại tiếp $\mathrm{\Delta }ABC.$

- Vẽ đường tròn tâm $\left(O;R\right)$ tâm $O$   bán kính $R=OA$,  ta được đường tròn ngoại tiếp tam giác đều  $ABC$ vì nó đi qua ba đỉnh của tam giác đều $ABC.$  

Ta có $A{A}^{\prime }$ là đường cao của tam giác đều $ABC$ cạnh $a$ ,

$\Rightarrow A{A}^{\prime }={\displaystyle \frac{a\sqrt{3}}{2}};R=OA={\displaystyle \frac{2}{3}}A{A}^{\prime }$$={\displaystyle \frac{a}{\sqrt{3}}}.$

Vậy bán kính  của đường tròn ngoại tiếp $R={\displaystyle \frac{a}{\sqrt{3}}}.$

c) Vẽ đường tròn $\left(O;r\right)$ nội tiếp:

Tại  tâm $O$ vẽ  bán kính $r=O{A}^{\prime }$ . Ta được đường tròn nội tiếp tam giác $ABC$ vì $\left(O;r\right)$ tiếp xúc với $AB;BC;AC$ theo thứ tự tại $C^{\prime },A^{\prime },B^{\prime }.$

Mà $O{A}^{\prime }={\displaystyle \frac{1}{3}}.A{A}^{\prime }={\displaystyle \frac{a}{2\sqrt{3}}}cm$

Vậy $r={\displaystyle \frac{a}{2\sqrt{3}}}.$

d) Vẽ tiếp tam giác đều $IJK$ ngoại tiếp đường tròn $\left(O;R\right)$ :

Vẽ ba tiếp tuyến với đường tròn $\left(O;R\right)$ tại $A,B,C$. Giao điểm của chúng là $I;J;K.$Ta được tam giác đều $IJK$ngoại tiếp đường tròn $\left(O;R\right)$. $IJK$ là tam giác đều  có các góc bằng  ${60}^{\circ }.$

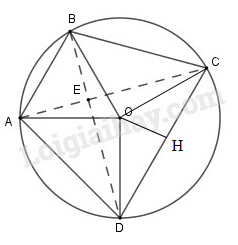
Trên đường tròn bán kính $R$ lần lượt đặt theo cùng một chiều, kể từ điểm $A$, ba cung $AB,BC,CD$ sao cho sđ$\stackrel{⏜}{AB}={60}^o$, sđ$\stackrel{⏜}{BC}={90}^o$, sđ$\stackrel{⏜}{CD}={120}^o$.

a) Tứ giác $ABCD$ là hình gì ?

d) Chứng minh rằng hai đường chéo của tứ giác $ABCD$ vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác $ABCD$ theo $R$.

Phương pháp giải:

a) Sử dụng số đo cả đường tròn bằng ${360}^{\circ }$ để tính số đo cung $AD$.

Sử dụng dấu hiệu nhận biết tứ giác có hai cạnh đáy song song và hai cạnh bên (hoặc hai góc ở đáy) bằng nhau.

b) Sử dụng: Số đo góc có đỉnh bên trong đường tròn bẳng nửa tổng số đo hai cung bị chắn

c) Sử dụng định lý Pytago và tính chất tam giác đều.

Trả lời:

a) Xét cung $DA$ , ta có : 

sđ$\stackrel{⏜}{DA}=$ ${360}^{\circ }-$ (sđ $\stackrel{⏜}{AB}+$ sđ$\stackrel{⏜}{BC}+$ sđ$\stackrel{⏜}{CD}$) $={360}^{\circ }-{270}^{\circ }={90}^{\circ }.$

Vậy sđ$\stackrel{⏜}{DA}={90}^{\circ }$ ta có : sđ$\stackrel{⏜}{BC}$ = sđ$\stackrel{⏜}{DA}$

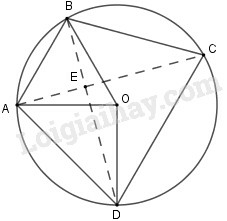
 $\Rightarrow \widehat{ACD}=\widehat{BAC}={\displaystyle \frac{1}{2}}$ sđ$\stackrel{⏜}{AD}$. Do đó, ta có $AB//DC$ và $\stackrel{⏜}{BC}=\stackrel{⏜}{AD}$ $\Rightarrow BC=DA.$

Vậy tứ giác$ABCD$ là hình thang cân.

b) Gọi $E$ là giao điểm của hai đường chéo $AC$ và $BD$. Góc  $AEB$ có đỉnh  nằm bên trong đường tròn nên ta có:

$\widehat{AEB}={\displaystyle \frac{1}{2}}$ (sđ $\stackrel{⏜}{AB}$ + sđ $\stackrel{⏜}{CD}$). Từ giả thiết ta có sđ$\stackrel{⏜}{CD}$$={120}^{\circ };$ sđ$\stackrel{⏜}{AB}$ $={60}^{\circ }$

Vậy  $\widehat{AEB}={90}^{\circ }\Rightarrow AC\mathrm{\perp }BD.$

c) Ta có $\widehat{AOB}=$ sđ$\stackrel{⏜}{AB}$ $={60}^{\circ }$ là góc ở tâm và  $OA=OB=AB$

$\Rightarrow \mathrm{\Delta }\mathrm{A}OB$ là tam giác đều.

Vậy  $AB=R.$

Ta có $\widehat{AOD}=$ sđ $\stackrel{⏜}{AD}$ $={90}^{\circ }$và $OA=OD=R\Rightarrow \mathrm{\Delta }AOD$ là tam giác vuông cân.

$A{D}^2=O{A}^2+O{D}^2=2R^2.$ Vậy $AD=R\sqrt{2}$ và $BC=AD=R\sqrt{2},$ vì $ABCD$ là hình thang cân.

Kẻ $OH\mathrm{\perp }CD$ tại $H$

Vì sđ$\stackrel{⏜}{CD}$ $={120}^{\circ }$ $\Rightarrow \widehat{COD}={120}^0.$

Lại có $\mathrm{\Delta }DOC$ cân tại $O$ có $OH$ là đường cao nên $OH$ cũng là đường phân giác

$\Rightarrow \widehat{HOC}=\widehat{DOC}:2={120}^0:2={60}^0.$

Xét $\mathrm{\Delta }OCH$ vuông tại $H$ ta có:

$HC=OC.\sin \widehat{COH}={\displaystyle \frac{R\sqrt{3}}{2}}.$

Mà $H$ là trung điểm của $CD$ (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).

$\Rightarrow CD=2.CH=R\sqrt{3}.$

Vậy $AB=R;DC=R\sqrt{3};BC=AD=R\sqrt{2}$