Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 10. Diện tích hình tròn, quạt tròn trang 119,120,121,122 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 10. Diện tích hình tròn, quạt tròn
Phần câu hỏi bài 10 trang 119, 120 Vở bài tập toán 9 tập 2
Câu 23
Diện tích hình vành khăn giữa hai đường tròn đồng tâm và là . Tiếp tuyến tại của đường tròn cắt đường tròn tại và . Độ dài dây cung của đường tròn lớn tiếp xúc với đường tròn nhỏ là:
(A) (B)
(C) (D)
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
+ Sử dụng công thức tính diện tích hình tròn bán kính là , từ đó suy ra diện tích hình vành khăn
+ Sử dụng quan hệ giữa đường kính và dây cung, định lý Pytago để tính toán
Trả lời:
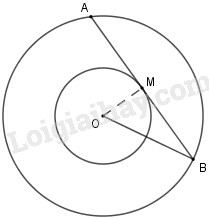
Diện tích hình tròn là , diện tích hình tròn là
Suy ra diện tích hình vành khăn là
Từ bài cho ta có
Xét đường tròn có là tiếp tuyến tại
Xét có nên là trung điểm (quan hệ giữa dây và đường kính), suy ra
Xét tam giác vuông tại , theo định lý Pytago ta có mà (cmt) và (cmt) nên
Chọn C.
Câu 24
Một hình vuông cạnh a và một đường tròn bán kính r có chu vi bằng nhau. Tỉ số giữa diện tích hình tròn và diện tích hình vuông là:
(A) (B)
(C) (D)
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
+ Hình vuông cạnh có chu vi là và diện tích là
+ Đường tròn bán kính có chu vi và diện tích hình tròn là
Trả lời:
Ta có:
Hình vuông cạnh có chu vi là và diện tích là và đường tròn bán kính có chu vi và diện tích hình tròn là .
Vì theo giả thiết thì hình vuông và đường tròn có chu vi bằng nhau nên
Tỉ số giữa diện tích hình tròn và diện tích hình vuông là (vì (cmt))
Chọn A.
Chân một đống cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi là . Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông ?
Phương pháp giải:
+ Tính bán kính đường tròn từ công thức chu vi
+ Tính diện tích hình tròn bán kính theo công thức
Trả lời
Từ công thức
Khi đó, diện tích chân đống cát là
Tính diện tích một hình quạt tròn có bán kính , số đo cung là o
Phương pháp giải:
Hình quạt tròn bán kính , cung có diện tích
Trả lời:
Theo công thức , ta có diện tích hình quạt tròn là :
Diện tích hình tròn sẽ thay đổi như thế nào nếu:
a) Bán kính tăng gấp đôi ?
b) Bán kính tăng gấp ba ?
c) Bán kính tăng k lần ?
Phương pháp giải:
Sử dụng công thức tính diện tích hình tròn có bán kính là
Trả lời:
Giả sử hình tròn có bán kính thì
a) Bán kính là thì
Vậy nếu bán kính tăng gấp đôi thì diện tích tăng gấp 4 lần.
b) Bán kính là thì
Vậy nếu bán kính tăng gấp ba thì diện tích tăng gấp 9 lần.
c) Bán kính là thì
Vậy nếu bán kính tăng gấp k lần thì diện tích tăng gấp lần.
a) Vẽ hình 58 (tạo bởi các cung tròn) với và . Nêu cách vẽ:
b) Tính diện tích hình HOABINH (miền gạch chéo).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.
Phương pháp giải:
a) Vẽ các nửa đường tròn để tạo thành hình đã cho
b) Sử dụng công thức tính diện tích hình tròn bán kính là để suy ra diện tích miền gạch chéo
c) Sử dụng công thức tính diện tích hình tròn bán kính là
Trả lời:
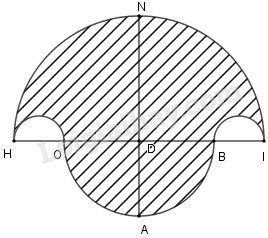
a) Cách vẽ :
- Vẽ đoạn thẳng .
- Vẽ đường trung trực của . Gọi là giao điểm của với
- Lấy làm tâm vẽ cung tròn với bán kính cắt tại và
- Lấy làm tâm vẽ cung tròn với bán kính về phía đối diện cung cắt tại và
- Lấy điểm chính giữa của làm tâm, vẽ cung tròn với bán kính bằng
- Lấy điểm chính giữa của làm tâm, vẽ cung tròn với bán kính bằng
b) Tính diện tích của hình gạch chéo :
Vì hình gạch chéo được tạo bởi các nửa đường tròn bán kính và
Ta có : (1)
( là diện tích nửa hình tròn đường kính
và (2)
(3)
Thay kết quả từ (2) và (3) vào (1), ta được
c) Gọi là diện tích hình tròn đường kính là bán kính.
Ta có : Bán kính
Vậy đường tròn đường kính NA (đpcm).
Bài 52 trang 122 Vở bài tập toán 9 tập 2
Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (h.59).
a) Tính diện tích của hình vành khăn theo R1 và R2 (giả sử R1 > R2)
b) Tính diện tích của hình vành khăn khi R1 = 10,5 cm, R2 = 7,8 cm.
Phương pháp giải:
Sử dụng công thức tính diện tích hình tròn bán kính là để suy ra diện tích hình vành khăn
Trả lời:
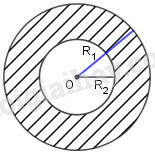
Gọi là diện tích hình vành khăn;
là diện tích hình tròn ;
là diện tích hình tròn ;
Mà và
Vậy diện tích hình vành khăn là
Lấy cạnh của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng . Cho biết cạnh . Hãy tính diện tích của hai hình viên phân được tạo thành.
Phương pháp giải:
+ Sử dụng công thức tính diện tích quạt tròn bán kính , số đo là
+ Công thức tính diện tích tam giác với là độ dài cạnh đáy, là chiều cao ứng với cạnh đáy.
Trả lời:
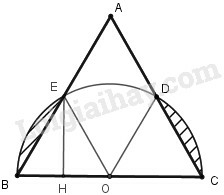
Gọi lần lượt là giao của hai cạnh với nửa đường tròn đường kính .
Nối tâm với và (h.60)
Xét ta có là bán kính của đường tròn đường kính và là tam giác đều.
Vậy
Ta có :
Theo công thức tính diện tích hình quạt ta có :
, trong đó
Vậy
trong đó vì đều.
Mà
Vậy diện tích hình viên phân
Tương tự, ta có vì nên và .
Suy ra
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.