Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 7. Tứ giác nội tiếp trang 109,110,111,112 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 7. Tứ giác nội tiếp

Phần câu hỏi bài 7 trang 109, 110 Vở bài tập toán 9 tập 2

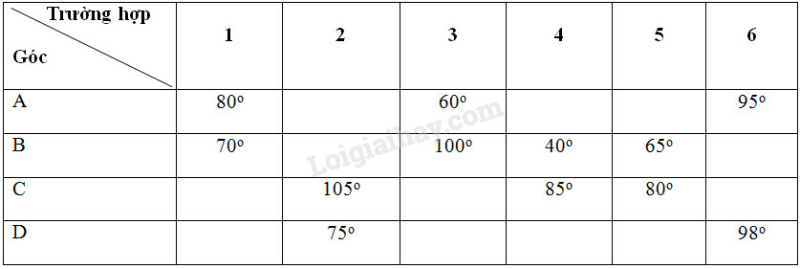
Phương pháp giải:

Sử dụng: Nếu $ABCD$ là tứ giác nội tiếp thì $\hat{A}+\hat{C}={180}^{\circ };\hat{B}+\hat{D}={180}^{\circ }$

Và tổng bốn góc trong tứ giác luôn bằng ${360}^{\circ }.$

Trả lời:

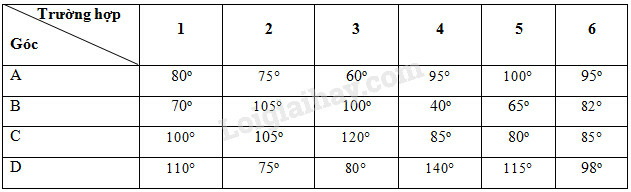
Câu 18

Hãy điền những từ còn thiếu trong câu sau:

Hình thang nội tiếp được trong đường tròn là……và…….

Phương pháp giải:

Sử dụng định lý: “Tứ giác có tổng hai góc đối bằng ${180}^{\circ }$ là tứ giác nội tiếp”

Trả lời:

Hình thang nội tiếp được trong đường tròn là hình thang cân và ngược lại.

Cho $ABCD$ là tứ giác nội tiếp đường tròn tâm $M$, biết $\widehat{DAB}={80}^0,$$\widehat{DAM}={30}^0,$$\widehat{BMC}={70}^0$. Hãy tính số đo góc $MAB;$$BCM;$$AMB;DMC;AMD;MCD$ và $BCD$. 

Phương pháp giải:

+ Sử dụng các định lý: “Trong tứ giác nội tiếp, tổng hai góc đối bằng ${180}^{\circ }$”; “Tổng ba góc trong tam giác bằng ${180}^{\circ }$”.

+ Sử dụng tính chất tam giác cân

Trả lời:

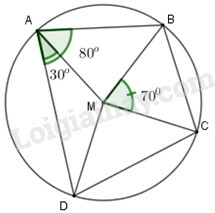
Nối tâm $M$ của đường tròn với các đỉnh $A,B,C,D.$

Vì $ABCD$ nội tiếp đường tròn ta có :

 $\widehat{DAB}+\widehat{BCD}={180}^{\circ }$$\iff \widehat{BCD}={180}^{\circ }-{80}^{\circ }={100}^{\circ };$

$\widehat{MAB}=\widehat{DAB}-\widehat{DAM}$$={80}^{\circ }-{30}^{\circ }={50}^{\circ }.$

+ Xét $\mathrm{\Delta }BMC$ cân vì $MB=MC$

Ta có $\widehat{MBC}=\widehat{BCM}$

$\Rightarrow 2\widehat{BCM}={180}^{\circ }-\widehat{BMC}$$={180}^{\circ }-{70}^{\circ }={110}^{\circ }.$ Vậy $\widehat{BCM}={55}^{\circ }.$

+ Xét $\mathrm{\Delta }BMA$ cân vì $MB=MA.$

Ta có $\widehat{MAB}=\widehat{ABM}$$\Rightarrow \widehat{AMB}={180}^{\circ }-2.\widehat{MAB}$$={180}^{\circ }-{2.50}^{\circ }={80}^{\circ }$ .

Vậy $\widehat{AMB}={80}^{\circ }.$

+ Xét $\mathrm{\Delta }DMA$ cân vì $MD=MA.$

Ta có  $\widehat{MAD}=\widehat{ADM}$$\Rightarrow \widehat{AMD}={180}^{\circ }-2.\widehat{ADM}$$={180}^{\circ }-{60}^{\circ }={120}^{\circ }.$

Vậy  $\widehat{AMD}={120}^{\circ }.$

Từ các kết quả trên ta có

$\widehat{DMC}={360}^{\circ }-\left(\widehat{AMD}+\widehat{AMB}+\widehat{BMC}\right)$$={360}^{\circ }-\left({120}^{\circ }+{80}^{\circ }+{70}^{\circ }\right)={90}^{\circ }$ 

Vậy  $\widehat{DMC}={90}^{\circ }$ 

Xét $\mathrm{\Delta }DMC$ cân vì $MD=MC.$ Ta có $\widehat{MCD}=\widehat{CDM}$

$\Rightarrow 2\widehat{MCD}={180}^{\circ }-\widehat{DMC}$$={180}^{\circ }-{90}^{\circ }={90}^{\circ }$.

Vậy $\widehat{MCD}={45}^{\circ },\widehat{BCD}={100}^{\circ }.$

Xem hình 48. Hãy tính số đo các góc của tứ giác ABCD.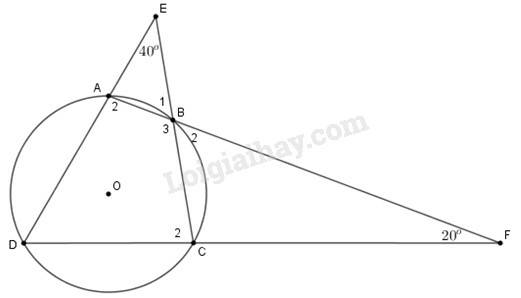

Phương pháp giải:

+ Sử dụng các định lý: “Trong tứ giác nội tiếp, tổng hai góc đối bằng ${180}^{\circ }$”; “Tổng ba góc trong tam giác bằng ${180}^{\circ }$” và “Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó”

+ Sử dụng tính chất hai góc kề bù 

Trả lời:

Xét $\mathrm{\Delta }ABE$ và $\mathrm{\Delta }CBF,$ ta có $\widehat{A_2}={40}^{\circ }+\widehat{B_1}\left(1\right)$ vì $\widehat{A_2}$ là góc ngoài tại đỉnh $E$ của $\mathrm{\Delta }ABE$.  

 $\widehat{C_2}=\hat{F}+\widehat{B_2}\left(2\right)$ vì góc ngoài của $\mathrm{\Delta }CBF.$

Cộng $\left(1\right)$ và $\left(2\right)$ và theo giả thiết ta có : $\widehat{A_2}+\widehat{C_2}={40}^{\circ }+\widehat{B_1}+\widehat{B_2}+\hat{F}\left(3\right)$

Vì $ABCD$ là tứ giác nội tiếp nên $\widehat{A_2}+\widehat{BCF}={180}^{\circ }$và $\widehat{B_1}=\widehat{B_2}$ vì hai góc đối đỉnh

Từ $\left(3\right)$ ta có ${180}^{\circ }={60}^{\circ }+2\widehat{B_1}\Rightarrow \widehat{B_1}={60}^{\circ }.$

Thay $\widehat{B_1},\widehat{B_2}$ vào (1) và (2) ta có : $\widehat{A_2}={40}^{\circ }+{60}^{\circ }={100}^{\circ };$

$\widehat{C_2}={20}^{\circ }+{60}^{\circ }={80}^{\circ };$ $\widehat{B_3}={180}^{\circ }-\widehat{B_1}={120}^{\circ }$

Vì $ABCD$ nội tiếp nên $\widehat{B_3}+\hat{D}={180}^{\circ }$ $\Rightarrow \hat{D}={180}^{\circ }-\widehat{B_3}={60}^{\circ }$

Vậy số đo các góc của tứ giác $ABCD$ là : $\widehat{A_2}={100}^{\circ };\widehat{C_2}={80}^{\circ };\widehat{B_3}={120}^{\circ };$$\hat{D}={60}^{\circ }.$

Cho tam giác đều $ABC$. Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A$, lấy điểm $D$ sao cho $DB=DC$ và $\widehat{BCD}={\displaystyle \frac{1}{2}}\widehat{ACB}.$

a) Chứng minh $ABCD$ là tứ giác nội tiếp.

b) Xác định tâm của đường tròn đi qua bốn điểm $A,B,C,D.$

Phương pháp giải:

Chứng minh tứ giác nội tiếp dựa vào dấu hiệu nhận biết “ tứ giác có tổng hai góc đối bằng  là tứ giác nội tiếp”

Trả lời:

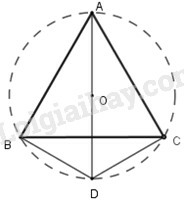
a) Theo giả thiết : $\widehat{DCB}={\displaystyle \frac{1}{2}}\widehat{ACB}={30}^{\circ }$       (1)

$\widehat{DCB}=\widehat{DBC}$ vì $\mathrm{\Delta }BDC$ cân tại D do $DB=DC$     (2)

Từ (1) và (2) $\Rightarrow \widehat{DCB}=\widehat{DBC}={30}^{\circ }$

Trong tứ giác $ABCD$ ta có : $\widehat{ABD}=\widehat{DBC}+\widehat{CBA}={30}^{\circ }+{60}^{\circ }$$={90}^{\circ };$

$\widehat{ACD}=\widehat{DCB}+\widehat{BCA}={30}^{\circ }+{60}^{\circ }$$={90}^{\circ }$

nên $\widehat{ABD}+\widehat{DCA}={180}^{\circ }.$ Vậy  tứ giác $ABCD$ là tứ giác nội tiếp ( hai góc đối nhau có tổng bằng ${180}^{\circ }$)

b) Vì $\widehat{ABD}=\widehat{ACD}={90}^{\circ }$ nên $AD$ là đường kính đường tròn ngoại tiếp tứ giác $ABCD.$

Vậy tâm đường tròn đi qua $4$ điểm $A,B,C,D$ là trực tâm của tam giác đều $ABC$ và là trung điểm của đoạn thẳng $AD.$

Cho hình bình hành $ABCD$. Đường tròn đi qua ba đỉnh $A,B,C$ cắt đường thẳng $CD$ tại $P$ khác $C$. Chứng minh $AP=AD$.

Phương pháp giải:

Sử dụng tính chất: Hai cung bị chắn giữa hai dây song song thì bằng nhau và tính chất hình bình hành.

Trả lời:

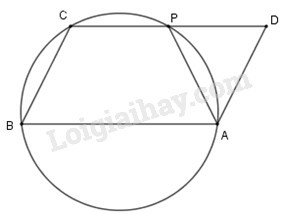
Từ $AB//CD\Rightarrow$$\stackrel{⏜}{AP}=\stackrel{⏜}{CB}$ (vì hai cung bị chắn giữa hai dây song song thì bằng nhau), suy ra  $AP=BC.\left(1\right)$

Từ giả thiết ta có $AD=BC$                (2)

Vậy từ (1) và (2) $\Rightarrow AP=AD.$