b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).

c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.

d) Vẽ đường tròn (O; r).

Phương pháp giải:

c) Sử dụng hai dây bằng nhau thì cách đều tâm.

Lời giải:

a)

b) Lục giác đều chứa 6 tam giác đều bằng nhau có cạnh = độ dài bán kính

Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)

Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm

c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lí liên hệ giữa dây cung và khoảng cách từ tâm đến dây)

Áp dụng định lí Pytago trong tam giác vuông OAH, ta có:

$O{H}^2+A{H}^2=O{A}^2$

$\Rightarrow r^2+1^2=2^2$

$\Rightarrow r^2=3$

$\Rightarrow r=\sqrt{3}$ cm

d) Vẽ đường tròn tâm O, bán kính $r=\sqrt{3}$ cm

b) Vẽ hình vuông nội tiếp đường tròn $(O)$ ở câu a)

c) Tính bán kính $r$ của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn $(O;r)$

Phương pháp giải:

+) Sử dụng compa và thước kẻ để vẽ hình.

+) Sử dụng định lý Pi-ta-go để tính $r.$

Lời giải:

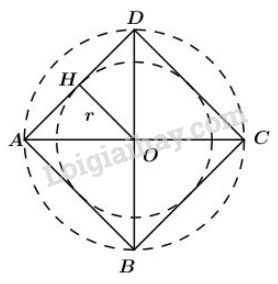
a) Chọn điểm $O$ làm tâm, mở compa có độ dài $2cm$ vẽ đường tròn tâm $O$, bán kính $2cm$: $(O;2cm).$

Vẽ bằng eke và thước thẳng. 

b) Vẽ đường kính $AC$ và $BD$ vuông góc với nhau. Nối $A$ với $B$, $B$ với $C$, $C$ với $D$, $D$ với $A$ ta được tứ giác $ABCD$ là hình vuông nội tiếp đường tròn $(O;2cm)$

c) Kẻ $OH\mathrm{\perp }AD.$

Khi đó ta có $OH$ là bán kính $r$ của đường tròn nội tiếp hình vuông $ABCD.$ Vì $AB=BC=CD=DA$ ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau và cùng bằng OH ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây) 

Ta có: $\mathrm{\Delta }OAD$ là tam giác vuông cân tại $O$ lại có $OH$ là đường cao $\Rightarrow H$ là trung điểm của $AD\Rightarrow OH=AH=HD.$

$\Rightarrow r=OH=AH.$

 Áp dụng định lý Pi-ta-go cho tam giác vuông $OHD$ ta có:

$O{H}^2+A{H}^2=O{A}^2$ $\iff r^2+r^2=2^2\Rightarrow 2r^2=4\Rightarrow r=\sqrt{2}(cm).$

Vẽ đường tròn $(O;\sqrt{2}cm)$. Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

b) Vẽ đường tròn $(O;R)$ ngoại tiếp tam giác đều $ABC$. Tính $R$.

c) Vẽ đường tròn $(O;r)$ nội tiếp tam giác đều $ABC$. Tính $r$.

d) Vẽ tiếp tam giác đều $IJK$ ngoại tiếp đường tròn $(O;R)$.

Phương pháp giải:

+) Sử dụng thước và compa để vẽ hình.

+) Tâm đường tròn ngoại tiếp là giao của 3 đường trung trực.

+) Tâm đường tròn nội tiếp là giao của 3 đường phân giác.

+) Sử dụng định lý Pi-ta-go và tính chất của tam giác đều để tính R và r.

Lời giải:

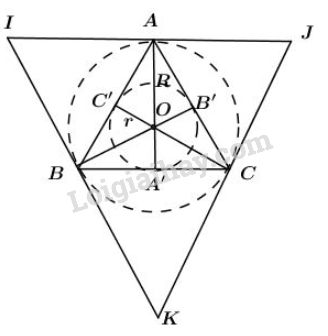
a) Vẽ tam giác đều $ABC$ có cạnh bằng $3cm$ (dùng thước có chia khoảng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) Gọi $A^{\prime };B^{\prime };C^{\prime }$ lần lượt là trung điểm của $BC;AC;AB.$

Tâm $O$ của đường tròn ngoại tiếp tam giác đều $ABC$ là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác $A{A}^{\prime };B{B}^{\prime };C{C}^{\prime }$ của tam giác đều $ABC$).

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính $R=OA=OB=OC$ ta được đường tròn ngoại tiếp tam giác ABC.

Tính $A{A}^{\prime }$:

Xét tam giác $A{A}^{\prime }C$ vuông tại $A^{\prime }$ có $AC=3;A^{\prime }C={\displaystyle \frac{3}{2}}$, theo định lý Pytago ta có $A{C}^2=A{A}^{\prime 2}+A^{\prime }{C}^2$$\Rightarrow A{A}^{\prime 2}=3^2-{\displaystyle \frac{3^2}{4}}={\displaystyle \frac{9}{4}}\Rightarrow A{A}^{\prime }={\displaystyle \frac{3\sqrt{3}}{2}}$

Theo cách dựng ta có O cũng là trọng tâm tam giác ABC nên $OA={\displaystyle \frac{2}{3}}A{A}^{\prime }$ 

Ta có bán kính đường tròn ngoại tiếp tam giác ABC là   $R=OA=$ ${\displaystyle \frac{2}{3}}$$A{A}^{\prime }$ = ${\displaystyle \frac{2}{3}}$. ${\displaystyle \frac{3\sqrt{3}}{2}}$ = $\sqrt{3}(cm)$.

c) Do tam giác ABC là tam giác đều các trung điểm A’; B’; C’ của các cạnh BC; CA; AB đồng thời là chân đường phân giác hạ từ A, B, C đến BC, AC, AB.

Đường tròn nội tiếp $(O;r)$ tiếp xúc ba cạnh của tam giác đều $ABC$ tại các trung điểm $A^{\prime },B^{\prime },C^{\prime }$ của các cạnh.

Hay đường tròn (O; r) là đường tròn tâm O; bán kính $r=O{A}^{\prime }=O{B}^{\prime }=O{C}^{\prime }.$

Ta có: $r=O{A}^{\prime }$$={\displaystyle \frac{1}{3}}$$A{A}^{\prime }$ $={\displaystyle \frac{1}{3}}.{\displaystyle \frac{3\sqrt{3}}{2}}$ $={\displaystyle \frac{\sqrt{3}}{2}}(cm).$

d) Vẽ các tiếp tuyến với đường tròn $(O;R)$ tại $A,B,C$. Ba tiếp tuyến này cắt nhau tại $I,J,K$. Ta có $∆IJK$ là tam giác đều ngoại tiếp $(O;R)$.  

Phương pháp giải:

+) Sử dụng compa và thước kẻ có chia độ dài để vẽ hình.

+) Sử dụng định lý Pi-ta-go để tính R.

Lời giải:

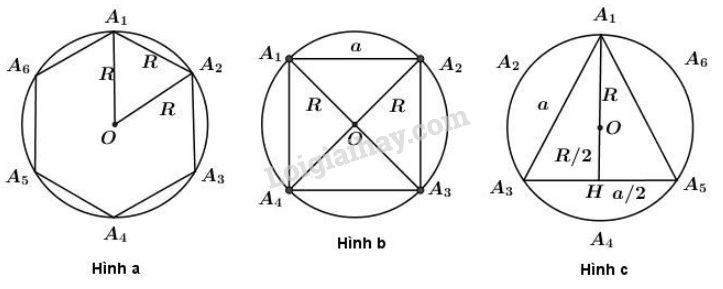
+) Hình a. 

Cách vẽ: vẽ đường tròn $(O;R)$. Trên đường tròn ta đặt liên tiếp các cung $\stackrel{⏜}{A_1{A}_2}$,  $\stackrel{⏜}{A_2{A}_3}$,...,$\stackrel{⏜}{A_6{A}_1}$ mà dây căng cung có độ dài bằng $R$. Nối $A_1$ với $A_2$, $A_2$ với $A_3$,…, $A_6$ với $A_1$ ta được hình lục giác đều $A_1$$A_2$$A_3$$A_4$$A_5$$A_6$ nội tiếp đường tròn

Tính bán kính:

Gọi $a_i$  là cạnh của đa giác đều có $i$ cạnh.

$a_6=R$ (vì $O{A}_1{A}_2$ là tam giác đều)

+) Hình b.

Cách vẽ:

+ Vẽ đường kính $A_1{A}_3$ của đường tròn tâm O.

+ Vẽ đường kính $A_2{A}_4\perp A_1{A}_3$

Tứ giác $A_1{A}_2{A}_3{A}_4$ có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.

Nối $A_1$ với $A_2;A_2$ với $A_3;A_3$ với $A_4;A_4$ với $A_1$ ta được hình vuông $A_1{A}_2{A}_3{A}_4$ nội tiếp đường tròn (O). 

Tính bán kính:

Gọi độ dài cạnh của hình vuông là $a.$

Vì hai đường chéo của hình vuông vuông góc với nhau nên xét tam giác vuông $O{A}_1{A}_2$ có

$a^2=R^2+R^2=2R^2\Rightarrow a=R\sqrt{2}$

+) Hình c: 

Cách vẽ như câu a) hình a. 

Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác $A_1{A}_3{A}_5$  như trên hình c.

Tính bán kính: 

Gọi độ dài cạnh của tam giác đều  là $a.$ 

$A_{1}H$ $=A_{1}O+OH=R+{\displaystyle \frac{R}{2}}$ =  ${\displaystyle \frac{3R}{2}}$

$A_{3}H$ $={\displaystyle \frac{A{A}^{\prime }}{2}}={\displaystyle \frac{a}{2}}$  

$A_1$$A_3=a$

Trong tam giác vuông $A_{1}H{A}_3$ ta có: $A_1{H}^2=A_1{A_3}^2-A_3{H}^2$.

Từ đó ${\displaystyle \frac{9R^2}{4}}$ = $a^2$ - ${\displaystyle \frac{a^2}{4}}$. 

$\Rightarrow a^2=3R^2\Rightarrow a=R\sqrt{3}$

a) Tứ giác $ABCD$ là hình gì?

b) Chứng minh hai đường chéo của tứ giác $ABCD$ vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác $ABCD$ theo $R$.

Phương pháp giải:

a) Dựa vào các dấu hiệu nhận biết của các hình tứ giác đặc biệt và các tứ giác nào có thể nội tiếp đường tròn để chứng minh tứ giác ABCD là hình gì.

Chú ý rằng: Hình thang nội tiếp được đường tròn là hình thang cân.

b) Số đo của góc có đỉnh nằm trong đường tròn bằng nửa số đo của tổng hai cung bị chắn.

c) Sử dụng định lý : "Số đo góc nội tiếp bằng nửa số đo cung bị chắn."

Sử dụng định lý Pytagoo để tính toán.

Lời giải:

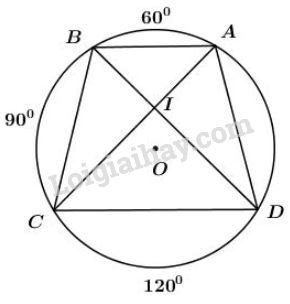
a) Xét đường tròn $(O)$ ta có:

${\displaystyle \widehat{BA\mathrm{D}}=\frac{{90}^0+{120}^0}{2}={105}^0}$ (góc nội tiếp chắn $\stackrel{⏜}{BCD}$)     (1)

${\displaystyle \widehat{A\mathrm{D}C}=\frac{{60}^0+{90}^0}{2}={75}^0}$ ( góc nội tiếp chắn $\stackrel{⏜}{ABC}$ )          (2)

Từ (1) và (2) có:

$\widehat{BA\mathrm{D}}+\widehat{A\mathrm{D}C}={105}^0+{75}^0={180}^0$ (3)

Mà hai góc này ở vị trí trong cùng phía 

Nên $AB//CD$. Do đó tứ giác $ABCD$ là hình thang, mà hình thang nội tiếp đường tròn là hình thang cân. 

Vậy $ABCD$ là hình thang cân suy ra ($BC=AD$ và $sđ\stackrel{⏜}{BC}$=$sđ\stackrel{⏜}{AD}$=${90}^0$)

b) Giả sử hai đường chéo $AC$ và $BD$ cắt nhau tại $I$.

$\widehat{CI\mathrm{D}}$ là góc có đỉnh nằm trong đường tròn, nên:

${\displaystyle \widehat{CI\mathrm{D}}}$ $={\displaystyle \frac{sđ\stackrel{⏜}{AB}+sđ\stackrel{⏜}{CD}}{2}}$$={\displaystyle \frac{{60}^0+{120}^0}{2}={90}^0}$

Vậy $AC\mathrm{\perp }BD.$ 

c) Vì $sđ\stackrel{⏜}{AB}={60}^0$ nên $\widehat{AOB}={60}^0$ (góc ở tâm)

$=>∆AOB$ đều, nên $AB=OA=OB=R.$

Vì  $sđ\stackrel{⏜}{BC}={90}^0\Rightarrow \widehat{BOC}={90}^0$ (góc ở tâm)

$\Rightarrow BC=\sqrt{O{B}^2+O{C}^2}=R\sqrt{2}.$

Kẻ $OH\mathrm{\perp }CD.$

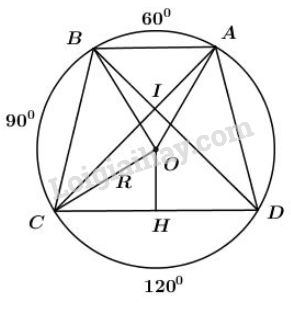
Tứ giác $ABCD$ là hình thang cân $\Rightarrow \widehat{BCD}=\widehat{ADC}={75}^0.$

Lại có $\mathrm{\Delta }BOC$ vuông cân tại $O\Rightarrow \widehat{BCO}={45}^0.$

$\Rightarrow \widehat{OCD}=\widehat{BCD}-\widehat{BCO}={75}^0-{45}^0={30}^0.$

Xét $\mathrm{\Delta }OCH$ vuông tại $H$ ta có:

$HC=OC.\cos \widehat{OCH}={\displaystyle \frac{R\sqrt{3}}{2}}.$

Mà $H$ là trung điểm của $CD$ (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).

$\Rightarrow CD=2.CH=R\sqrt{3}.$ 

Lý thuyết Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp

1. Định nghĩa 

a) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác này gọi là nội tiếp đường tròn.

b) Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn  nội tiếp đa giác và đa giác được gọi là ngoại tiếp đường tròn.

2. Định lí

Bất kì đa giác đều nào cũng có một đường tròn ngoại tiếp và một đường tròn nội tiếp 

Tâm của một đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp và được gọi là tâm của đa giác đều.

3. Công thức tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp đa giác đều.

Đa giác đều $n$ cạnh có độ dài mỗi cạnh là $a,R$ là bán kính đường tròn ngoại tiếp và $r$ là bán kính đường tròn nội tiếp đa giác. Ta có:

$R$ = ${\displaystyle \frac{a}{2sin{\displaystyle \frac{{180}^{\circ }}{n}}}}$; $r$ = ${\displaystyle \frac{a}{2tan{\displaystyle \frac{{180}^{\circ }}{n}}}}$.