Toán 10 Chân trời sáng tạo Bài 2: Định lí cosin và định lí sin

Hoàng Huyền Trang Ngày: 07-02-2023 Lớp 10

732

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2. Định lí cosin và định lí sin sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo Bài 2: Định lí cosin và định lí sin

HĐ Khởi động trang 65 Toán 10 Tập 1: Làm thế nào để tính độ dài cạnh chưa biết của hai tam giác dưới đây?

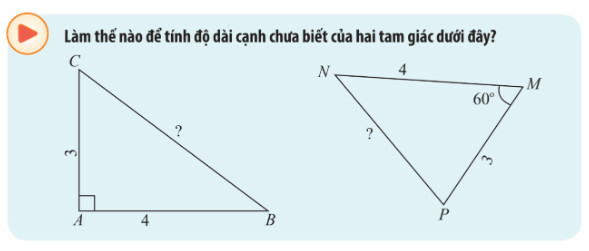
HĐ Khởi động trang 65 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Với $\hat{A} = 90^{o}$ ta sử dụng định lí Pytago.

Với $\hat{A} \neq 90^{o}$ : Áp dụng định lí cosin: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

Lời giải

Áp dụng định lí Pytago, ta có:

$\begin{array}{l} B C^{2} = A C^{2} + A B^{2} = 3^{2} + 4^{2} = 25 \\ \Rightarrow B C = 5 \end{array}$

Áp dụng định lí cosin trong tam giác MNP, ta có:

$N P^{2} = M N^{2} + M P^{2} - 2. M N . M P \cos M$

Mà $M N = 4, M P = 3, \hat{M} = 60^{o}$

$\begin{array}{l} \Rightarrow N P^{2} = 4^{2} + 3^{2} - 2.4.3 \cos 60^{o} = 13 \\ \Leftrightarrow N P = \sqrt{13} \approx 3, 6 \end{array}$

1. Định lí cosin trong tam giác

HĐ Khám phá 1 trang 66 Toán 10 Tập 1: a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và $\hat{C} \geq \hat{B} .$ Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.

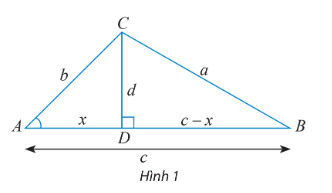
HĐ Khám phá 1 trang 66 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ theo gợi ý sau:

Xét tam giác vuông BCD, ta có: $a^{2} = d^{2} + (c - x)^{2} = d^{2} + x^{2} + c^{2} - 2 x c$ (1)

Xét tam giác vuông ACD, ta có: $b^{2} = d^{2} + x^{2} \Rightarrow d^{2} = b^{2} - x^{2}$ (2)

$\cos A = \frac{?}{b} \Rightarrow ? = b \cos A .$ (3)

Thay (2) và (3) vào (1), ta có: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

Lưu ý: Nếu $\hat{B} > \hat{C}$ thì ta vẽ đường cao BD và chứng minh tương tự.

b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:

$a^{2} = b^{2} + c^{2} - 2 b c \cos A$

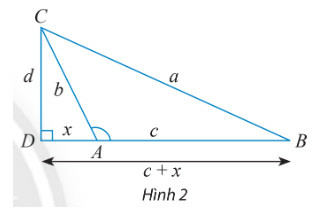
HĐ Khám phá 1 trang 66 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Lưu ý: Vì A là góc tù nên $\cos A = - \frac{x}{b} .$

c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ có thể viết là $a^{2} = b^{2} + c^{2} .$

Lời giải

a) ? = x vì $\cos A = \frac{A D}{A C} = \frac{x}{b} \Rightarrow ? = x .$

b) Xét tam giác vuông BCD, ta có: $a^{2} = d^{2} + (c + x)^{2} = d^{2} + x^{2} + c^{2} + 2 x c$ (1)

Xét tam giác vuông ACD, ta có: $b^{2} = d^{2} + x^{2} \Rightarrow d^{2} = b^{2} - x^{2}$ (2)

$\cos A = - \cos \hat{D A C} = - \frac{x}{b} \Rightarrow x = - b \cos A .$ (3)

Thay (2) và (3) vào (1), ta có: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

c) Ta có: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

Mà $\hat{A} = 90^{o} \Rightarrow \cos A = \cos 90^{o} = 0.$

$\Rightarrow a^{2} = b^{2} + c^{2}$

Câu hỏi trang 67 Toán 10

Thực hành 1 trang 67 Toán 10 Tập 1: Tính các cạnh và các góc chưa biết của tam giác ABC trong hình 4.

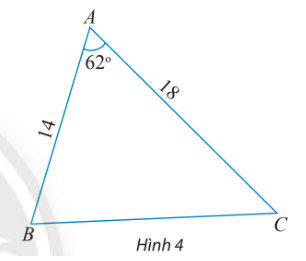
Thực hành 1 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Áp dụng định lí cosin trong tam giác ABC, ta có:

$\begin{array}{l} B C^{2} = A C^{2} + A B^{2} - 2 A C . A B \cos A \\ \cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C}; \cos C = \frac{A C^{2} + B C^{2} - A B^{2}}{2. A C . B C} \end{array}$

Lời giải

Áp dụng định lí cosin trong tam giác ABC, ta có:

$B C^{2} = A C^{2} + A B^{2} - 2 A C . A B \cos A$

Mà $A B = 14, A C = 18, \hat{A} = 62^{o}$

$\begin{array}{l} \Rightarrow B C^{2} = 18^{2} + 14^{2} - 2.18.14 \cos 62^{o} \approx 283, 3863 \\ \Leftrightarrow B C \approx 16, 834 \end{array}$

Lại có: Từ định lí cosin ta suy ra:

$\cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C}; \cos C = \frac{A C^{2} + B C^{2} - A B^{2}}{2. A C . B C}$

$\Rightarrow {\begin{cases} \cos B = \frac{14^{2} + 16, 834^{2} - 18^{2}}{2.14.16, 834} \approx 0, 3297 \\ \cos C = \frac{18^{2} + 16, 834^{2} - 14^{2}}{2.18.16, 834} \approx 0, 6788 \end{cases}$

$\Rightarrow {\begin{cases} \hat{B} \approx 70^{o} 45^{'} \\ \hat{C} \approx 47^{o} 15^{'} \end{cases}$

Vậy $B C \approx 16, 834; \hat{B} \approx 70^{o} 45^{'}; \hat{C} \approx 47^{o} 15^{'} .$

Vận dụng 1 trang 67 Toán 10 Tập 1: Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc $70^{o}$ (Hình 5).

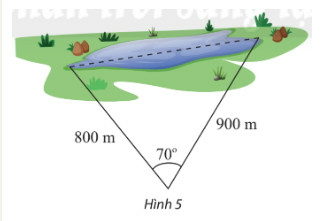
Vận dụng 1 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Áp dụng định lí cosin $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

Lời giải

Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:

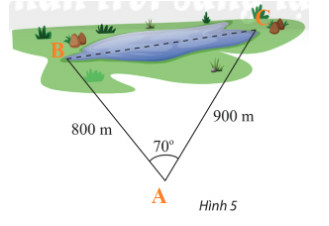
Vận dụng 1 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Áp dụng định lí cosin trong tam giác ABC, ta có:

$B C^{2} = A C^{2} + A B^{2} - 2 A C . A B \cos A$

Mà $A B = 800, A C = 900, \hat{A} = 70^{o}$

$\begin{array}{l} \Rightarrow B C^{2} = 900^{2} + 800^{2} - 2.900.800 \cos 70^{o} \approx 957490, 9936 \\ \Leftrightarrow B C \approx 987, 5147 \end{array}$

Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 987,5147 m.

2. Định lí sin trong tam giác

HĐ Khám phá 2 trang 67 Toán 10 Tập 1: a) Cho tam giác ABC không phải là tam giác vuông có $B C = a, A C = b, A B = c$ và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.

i) Tính $\sin \hat{B D C}$ theo a và R.

ii) Tìm mối liên hệ giữa hai góc $\hat{B A C}$ và $\hat{B D C}$ . Từ đó chứng minh rằng $2 R = \frac{a}{\sin A} .$

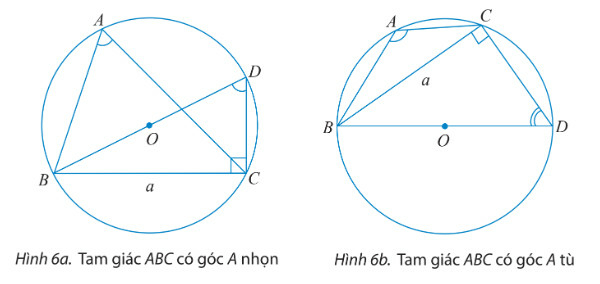
HĐ Khám phá 2 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức $2 R = \frac{a}{\sin A} .$

Lời giải

a) Tam giác BDC vuông tại C nên $\sin \hat{B D C} = \frac{B C}{B D} = \frac{a}{2 R} .$

TH1: Tam giác ABC có góc A nhọn

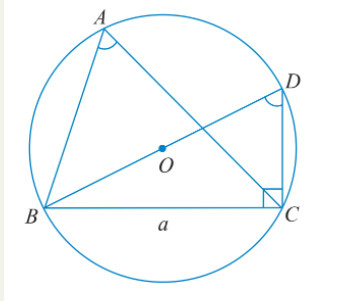
HĐ Khám phá 2 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

$\hat{B A C} = \hat{B D C}$ do cùng chắn cung nhỏ BC.

$\Rightarrow \sin \hat{B A C} = \sin \hat{B D C} = \frac{a}{2 R} .$

TH2: Tam giác ABC có góc A tù

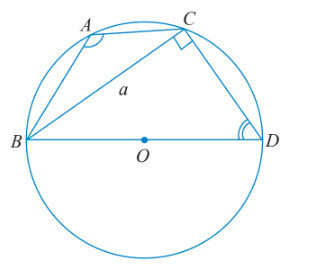
HĐ Khám phá 2 trang 67 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 3)

$\hat{B A C} + \hat{B D C} = 180^{o}$ do ABDC là tứ giác nội tiếp (O).

$\Rightarrow \sin \hat{B A C} = \sin (180^{o} - \hat{B A C}) = \sin \hat{B D C} = \frac{a}{2 R} .$

Vậy với góc A nhọn hay tù ta đều có $2 R = \frac{a}{\sin A} .$

b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).

Khi đó ta có: $\sin A = \sin 90^{o} = 1$ và $a = B C = 2 R$

Do đó ta vẫn có công thức: $2 R = \frac{a}{\sin A} .$

Thực hành 2 trang 68 Toán 10 Tập 1: Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.

Thực hành 2 trang 68 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Áp dụng định lí sin cho tam giác MNP:

$\frac{M N}{\sin P} = \frac{M P}{\sin N} = \frac{N P}{\sin M}$

Lời giải

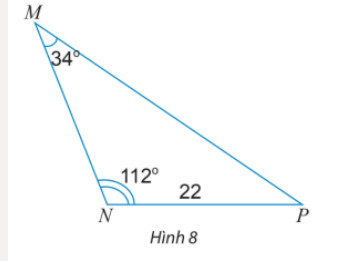
Ta có: $N P = 22, \hat{P} = 180^{o} - (112^{o} + 34^{o}) = 34^{o}$

Áp dụng định lí sin, ta có:

$\frac{M N}{\sin P} = \frac{M P}{\sin N} = \frac{N P}{\sin M}$

Suy ra:

$M P = \frac{N P . \sin N}{\sin M} = \frac{22. \sin 112^{o}}{\sin 34^{o}} \approx 36, 48$

$M N = \frac{N P . \sin P}{\sin M} = \frac{22. \sin 34^{o}}{\sin 34^{o}} = 22.$

Vận dụng 2 trang 69 Toán 10 Tập 1: Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như Hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?

Vận dụng 2 trang 68 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

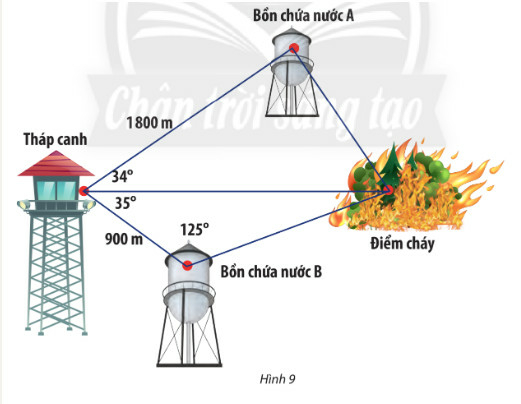
Áp dụng định lí sin, tính khoảng cách từ bồn chứa nước A đến đám cháy.

Áp dụng định lí cosin, tính khoảng cách từ bồn chứa nước B đến đám cháy.

Lời giải

Đặt các điểm A, B, C, D lần lượt là vị trí bồn chứa nước A, bồn chứa nước B, tháp canh và đám cháy.

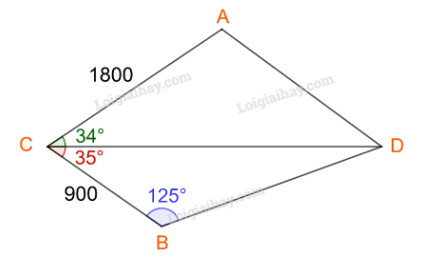
Vận dụng 2 trang 68 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có: $C B = 900, \hat{C D B} = 180^{o} - (125^{o} + 35^{o}) = 20^{o}$

Áp dụng định lí sin trong tam giác CBD, ta có:

$\frac{C B}{\sin D} = \frac{B D}{\sin C} = \frac{C D}{\sin B}$

Suy ra:

$B D = \frac{C B . \sin C}{\sin D} = \frac{900. \sin 35^{o}}{\sin 20^{o}} \approx 1509, 3$

$C D = \frac{C B . \sin B}{\sin D} = \frac{900. \sin 125^{o}}{\sin 20^{o}} = 2155, 5$

Áp dụng định lí cosin trong tam giác ACD ta có:

$\begin{array}{l} A D^{2} = A C^{2} + C D^{2} - 2. A C . C D . \cos \hat{A C D} \\ \Leftrightarrow A D^{2} = 1800^{2} + 2155, 5^{2} - 2.1800.2155, 5. \cos 34^{o} \approx 1453014, 5 \\ \Leftrightarrow A D \approx 1205, 4 \end{array}$

Vì $A D < B D$ nên khoảng cách từ bồn chứa nước A đến đám cháy là ngắn hơn.

Vậy nên dẫn nước từ bồn chứa nước A để dập tắt đám cháy nhanh hơn.

3. Các công thức tính diện tích tam giác

Câu hỏi trang 70 Toán 10

HĐ Khám phá 3 trang 70 Toán 10 Tập 1: Cho tam giác ABC như Hình 10.

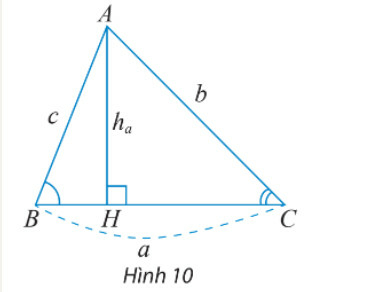
HĐ Khám phá 3 trang 70 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Viết công thức tính diện tích S của tam giác ABC theo a và $h_{a}$

b) Tính $h_{a}$ theo b và sinC.

c) Dùng hai kết quả trên để chứng minh công thức $S = \frac{1}{2} a b \sin C$

d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức $S = \frac{a b c}{4 R}$

Lời giải

a) Diện tích S của tam giác ABC là: $S = \frac{1}{2} a . h_{a}$

b) Xét tam giác vuông AHC ta có: $\sin C = \frac{A H}{A C} = \frac{h_{a}}{b}$

$\Rightarrow h_{a} = b . \sin C$

c) Thay $h_{a} = b . \sin C$ vào công thức diện tích, ta được: $S = \frac{1}{2} a b \sin C$

d) Theo định lí sin ta có: $\frac{c}{\sin C} = 2 R \Rightarrow \sin C = \frac{c}{2 R}$

Thay vào công thức ở c) ta được: $S = \frac{1}{2} a b \frac{c}{2 R} = \frac{a b c}{4 R} .$

HĐ Khám phá 4 trang 70 Toán 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).

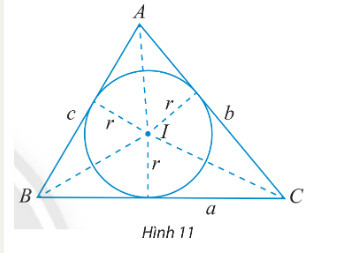
HĐ Khám phá 4 trang 70 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.

b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: $S = \frac{r (a + b + c)}{2}$

Lời giải

a) Diện tích $S_{1}$ của tam giác IAB là: $S_{1} = \frac{1}{2} r . A B = \frac{1}{2} r . c$

Diện tích $S_{2}$ của tam giác IAC là: $S_{2} = \frac{1}{2} r . A C = \frac{1}{2} r . b$

Diện tích $S_{3}$ của tam giác IBC là: $S_{3} = \frac{1}{2} r . B C = \frac{1}{2} r . a$

b) Diện tích S của tam giác ABC là:

$\begin{array}{l} S = S_{1} + S_{2} + S_{3} = \frac{1}{2} r . c + \frac{1}{2} r . b + \frac{1}{2} r . a = \frac{1}{2} r . (c + b + a) \\ \Leftrightarrow S = \frac{r (a + b + c)}{2} \end{array}$

Thực hành 3 trang 71 Toán 10 Tập 1: Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a) Các cạnh $b = 14, c = 35$ và $\hat{A} = 60^{o}$

b) Các cạnh $a = 4, b = 5, c = 3$

Phương pháp giải:

a) Áp dụng công thức: $S = \frac{1}{2} b c \sin A$

b) Áp dụng công thức Heron $S = \sqrt{p (p - a) (p - b) (p - c)}$

Lời giải

a) Áp dụng công thức: $S = \frac{1}{2} b c \sin A$ , ta có:

$S = \frac{1}{2} .14 .35 . \sin 60^{o} = \frac{1}{2} .14 .35 . \frac{\sqrt{3}}{2} \approx 212, 2$

b) Ta có: $p = \frac{1}{2} . (4 + 5 + 3) = 6$

Áp dụng công thức Heron, ta có:

$S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{6 (6 - 4) (6 - 5) (6 - 3)} = 6.$

Câu hỏi trang 72 Toán 10

Vận dụng 3 trang 72 Toán 10 Tập 1: Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là $48^{o}$ và $105^{o}$ (Hình 12).

Vận dụng 3 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

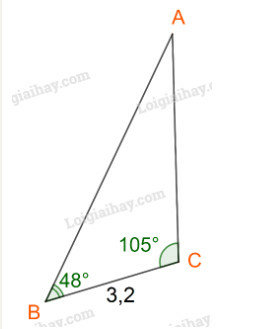
Vận dụng 3 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Bước 1: Áp dụng định lí sin tính AC.

Bước 2: Tính diện tích tam giác ABC bằng công thức $S = \frac{1}{2} a b \sin C$

Lời giải

Kí hiệu các điểm A, B, C như hình dưới

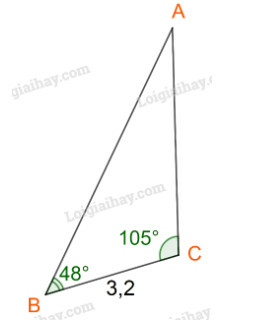
Vận dụng 3 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 3)

Đặt $A B = c, A C = b, B C = a .$

Ta có: $B C = 3, 2; \hat{A} = 180^{o} - (48^{o} + 105^{o}) = 27^{o}$

Áp dụng định lí sin, ta có:

$\frac{b}{\sin B} = \frac{a}{\sin A} \Rightarrow A C = b = \frac{a . \sin B}{\sin A} = \frac{3, 2. \sin 48^{o}}{\sin 105^{o}} \approx 2, 46 (m)$

Áp dụng công thức $S = \frac{1}{2} a b \sin C$ ta có:

$S = \frac{1}{2} .3, 2.2, 46 \sin 105^{o} \approx 1, 9 (m^{2})$

Bài tập

Bài 1 trang 72 Toán 10 Tập 1: Tính độ dài cạnh x trong các tam giác sau:

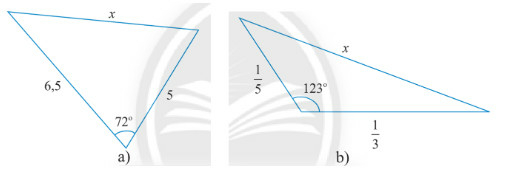
Bài 1 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Áp dụng định lí cosin, tính x bằng công thức: $x^{2} = 6, 5^{2} + 5^{2} - 2.6, 5.5. \cos 72^{o}$

Lời giải

a) Áp dụng định lí cosin, ta có:

$\begin{array}{l} x^{2} = 6, 5^{2} + 5^{2} - 2.6, 5.5. \cos 72^{o} \approx 47, 16 \\ \Leftrightarrow x \approx 6, 87 \end{array}$

b) Áp dụng định lí cosin, ta có:

$\begin{array}{l} x^{2} = {(\frac{1}{5})}^{2} + {(\frac{1}{3})}^{2} - 2. \frac{1}{5} . \frac{1}{3} . \cos 123^{o} \approx 0, 224 \\ \Leftrightarrow x \approx 0, 473 \end{array}$

Bài 2 trang 72 Toán 10 Tập 1: Tính độ dài cạnh c trong tam giác ABC ở Hình 14.

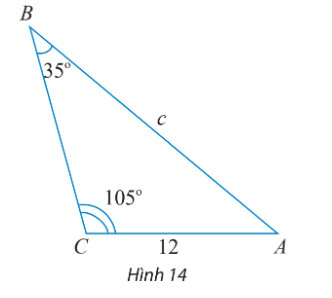
Bài 2 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Áp dụng định lí sin:

$\frac{c}{\sin 105^{o}} = \frac{12}{\sin 35^{o}}$

Lời giải

Áp dụng định lí sin, ta có:

$\frac{c}{\sin 105^{o}} = \frac{12}{\sin 35^{o}} \Rightarrow c = \frac{12. \sin 105^{o}}{\sin 35^{o}} \approx 3, 37$

Bài 3 trang 72 Toán 10 Tập 1: Cho tam giác ABC, biết cạnh $a = 152, \hat{B} = 79^{o}, \hat{C} = 61^{o} .$ Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.

Phương pháp giải

Áp dụng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

Lời giải

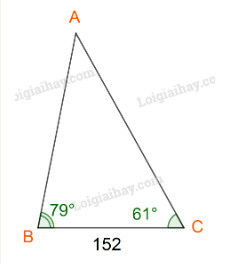
Bài 3 trang 72 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Đặt $A B = c, A C = b, B C = a .$

Ta có: $a = 152; \hat{A} = 180^{o} - (79^{o} + 61^{o}) = 40^{o}$

Áp dụng định lí sin, ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

Suy ra:

$\begin{array}{l} A C = b = \frac{a . \sin B}{\sin A} = \frac{152. \sin 79^{o}}{\sin 40^{o}} \approx 232, 13 \\ A B = c = \frac{a . \sin C}{\sin A} = \frac{152. \sin 61^{o}}{\sin 40^{o}} \approx 206, 82 \\ R = \frac{a}{\sin A} = \frac{152}{\sin 40^{o}} \approx 236, 47 \end{array}$

Câu hỏi trang 73 Toán 10

Bài 4 trang 73 Toán 10 Tập 1: Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

Bài 4 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Áp dụng định lí cosin để tính góc:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} .$

Lời giải

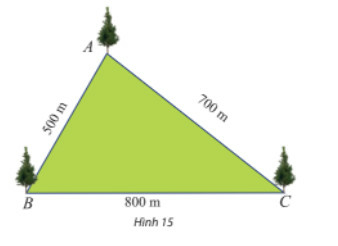
Đặt $a = B C, b = A C, c = A B$

Ta có: $a = 800, b = 700, c = 500.$

Áp dụng định lí cosin, ta có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} .$

Suy ra:

$\begin{array}{l} \cos A = \frac{700^{2} + 500^{2} - 800^{2}}{2.700.500} = \frac{1}{7} \Rightarrow \hat{A} = 81^{o} 47^{'} 12, 44^{″}; \\ \cos B = \frac{500^{2} + 800^{2} - 700^{2}}{2.500.800} = \frac{1}{2} \Rightarrow \hat{B} = 60^{o}; \\ \cos C = \frac{800^{2} + 700^{2} - 500^{2}}{2.800.700} = \frac{11}{14} \Rightarrow \hat{C} = 38^{o} 12^{'} 47, 56^{″} . \end{array}$

Vậy $\hat{A} = 81^{o} 47^{'} 12, 44^{″}; \hat{B} = 60^{o}; \hat{C} = 38^{o} 12^{'} 47, 56^{″} .$

Bài 5 trang 73 Toán 10 Tập 1: Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là $35^{o} .$

Bài 5 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Tính diện tích bằng công thức: $S = \frac{1}{2} b c \sin A$

Lời giải

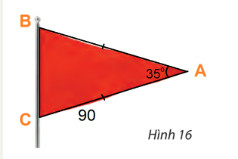
Bài 5 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Kí hiệu các điểm A, B, C như hình trên.

Từ giả thiết ta có: $A B = A C = 90, \hat{A} = 35^{o}$

Áp dụng công thức $S = \frac{1}{2} b c \sin A$ , ta có: $S = \frac{1}{2} .90 .90 . c \sin 35^{o} \approx 2323 (c m^{2})$

Bài 6 trang 73 Toán 10 Tập 1: Cho tam giác ABC có $A B = 6, A C = 8$ và $\hat{A} = 60^{o} .$

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC

Phương pháp giải

a) Tính diện tích bằng công thức: $S = \frac{1}{2} b c \sin A$

b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC

Lời giải

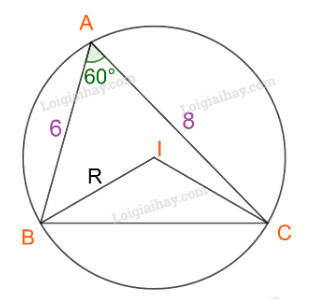
Đặt $a = B C, b = A C, c = A B .$

a) Áp dụng công thức $S = \frac{1}{2} b c \sin A$ , ta có: $S_{A B C} = \frac{1}{2} .8 .6 . \sin 60^{o} = \frac{1}{2} .8 .6 . \frac{\sqrt{3}}{2} = 12 \sqrt{3}$

b) Áp dụng định lí cosin cho tam giác ABC ta được:

$\begin{array}{l} B C^{2} = a^{2} = 8^{2} + 6^{2} - 2.8.6. \cos 60^{o} = 52 \\ \Rightarrow B C = 2 \sqrt{13} \end{array}$

Xét tam giác IBC ta có:

Góc $\hat{B I C} = 2. \hat{B A C} = 120^{o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$I B = I C = R = \frac{a}{\sin A} = \frac{2 \sqrt{13}}{\frac{\sqrt{3}}{2}} = \frac{4 \sqrt{39}}{3} .$

$\Rightarrow S_{I B C} = \frac{1}{2} . \frac{4 \sqrt{39}}{3} . \frac{4 \sqrt{39}}{3} \sin 120^{o} = \frac{52 \sqrt{3}}{3} .$

Bài 7 trang 73 Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.

a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.

b) Tính diện tích tam giác GBC.

Phương pháp giải

a) Tính r bằng công thức: $S = p . r$ . Trong đó S tính bởi công thức heron.

b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC

Lời giải

a) Đặt $a = B C, b = A C, c = A B .$

Ta có: $p = \frac{1}{2} (15 + 18 + 27) = 30$

Áp dụng công thức heron, ta có:

$S_{A B C} = \sqrt{30 (30 - 15) (30 - 18) (30 - 27)} = 90 \sqrt{2}$

Và $r = \frac{S}{p} = \frac{90 \sqrt{2}}{30} = 3 \sqrt{2}$

b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.

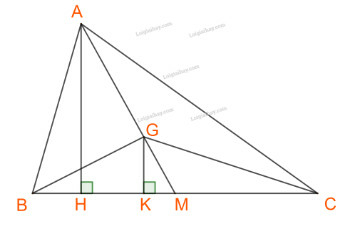
Bài 7 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

G là trọng tâm tam giác ABC nên $G M = \frac{1}{3} A M$

$\begin{array}{l} \Rightarrow G K = \frac{1}{3} . A H \\ \Rightarrow S_{G B C} = \frac{1}{3} . S_{A B C} = \frac{1}{3} .90 \sqrt{2} = 30 \sqrt{2} . \end{array}$

Xét tam giác IBC ta có:

Góc $\hat{B I C} = 2. \hat{B A C} = 120^{o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$I B = I C = R = \frac{a}{\sin A} = \frac{2 \sqrt{13}}{\frac{\sqrt{3}}{2}} = \frac{4 \sqrt{39}}{3} .$

$\Rightarrow S_{I B C} = \frac{1}{2} . \frac{4 \sqrt{39}}{3} . \frac{4 \sqrt{39}}{3} \sin 120^{o} = \frac{52 \sqrt{3}}{3} .$

Bài 8 trang 73 Toán 10 Tập 1: Cho $h_{a}$ là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: $h_{a} = 2 R . \sin B . \sin C$

Phương pháp giải

Bước 1: Tính $h_{a}$ theo b và sinC

Bước 2: Tính b theo R và sinB. Từ đó suy ra điều phải chứng minh. $h_{a} = 2 R \sin B \sin C .$

Lời giải

Đặt $a = B C, b = A C, c = A B$

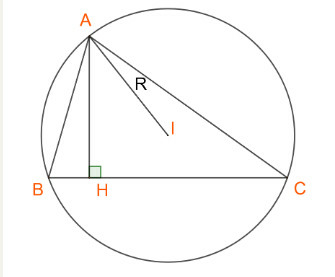
Bài 8 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Ta có: $\sin C = \frac{A H}{A C} = \frac{h_{a}}{b} \Rightarrow h_{a} = b . \sin C$

Theo định lí sin, ta có: $\frac{b}{\sin B} = 2 R \Rightarrow b = 2 R . \sin B$

$\Rightarrow h_{a} = 2 R . \sin B . \sin C$

Bài 9 trang 73 Toán 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C} .$

b) Biết rằng $S_{A B C} = 9 S_{B D E}$ và $D E = 2 \sqrt{2} .$ Tính $\cos B$ và bán kính đường tròn ngoại tiếp tam giác ABC.

Phương pháp giải

a) Tính diện tích bằng công thức $S = \frac{1}{2} a c . \sin B$

b) $\cos B = \frac{B D}{B A} = \frac{B E}{B C}$

Lời giải

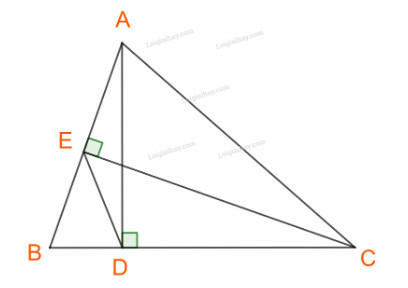
Bài 9 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Áp dụng công thức $S = \frac{1}{2} a c . \sin B$ cho tam giác ABC và BED, ta có:

$S_{A B C} = \frac{1}{2} . B A . B C . \sin B; S_{B E D} = \frac{1}{2} . . B E . B D . \sin B$

$\Rightarrow \frac{S_{B E D}}{S_{A B C}} = \frac{\frac{1}{2} . B E . B D . \sin B}{\frac{1}{2} . B A . B C . \sin B} = \frac{B E . B D}{B A . B C}$

b) Ta có: $\cos B = \frac{B D}{B A} = \frac{B E}{B C}$

Mà $\frac{S_{B E D}}{S_{A B C}} = \frac{1}{9} \Rightarrow \frac{B D}{B A} . \frac{B E}{B C} = \frac{1}{9}$

$\Rightarrow \cos B = \frac{B D}{B A} = \frac{B E}{B C} = \frac{1}{3}$

+) Xét tam giác ABC và tam giác DEB ta có:

$\frac{B E}{B C} = \frac{B D}{B A} = \frac{1}{3}$ và góc B chung

$\Rightarrow Δ A B C \sim Δ D E B$ (cgc)

$\Rightarrow \frac{D E}{A C} = \frac{1}{3} \Rightarrow A C = 3. D E = 3.2 \sqrt{2} = 6 \sqrt{2} .$

Ta có: $\cos B = \frac{1}{3} \Rightarrow \sin B = \sqrt{1 - {(\frac{1}{3})}^{2}} = \frac{2 \sqrt{2}}{3}$ (do B là góc nhọn)

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{A C}{\sin B} = 2 R \Rightarrow R = \frac{6 \sqrt{2}}{\frac{2 \sqrt{2}}{3}} : 2 = \frac{9}{2}$

Bài 10 trang 73 Toán 10 Tập 1: Cho tứ giác lồi ABCD có các đường chéo $A C = x, B D = y$ và góc giữa AC và BD bằng $α .$ Gọi S là diện tích của tứ giác ABCD.

a) Chứng minh $S = \frac{1}{2} x y . \sin α$

b) Nêu kết quả trong trường hợp $A C ⊥ B D .$

Phương pháp giải

a) Tính diện tích 4 tam giác nhỏ theo $\sin α$ .

Chú ý: $\sin (180^{o} - α) = \sin α$

b) $α = 90^{o}$ thì $\sin α = 1$

Lời giải

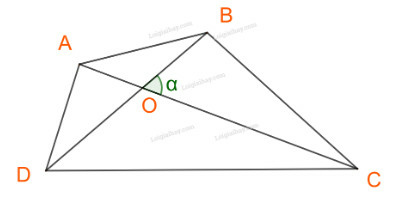
Bài 10 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Gọi O là giao điểm của AC và BD.

a) Áp dụng công thức $S = \frac{1}{2} a c . \sin B$ , ta có:

$\begin{array}{l} S_{O A D} = \frac{1}{2} . O A . O D . \sin α; S_{O B C} = \frac{1}{2} . . O B . O C . \sin α; \\ S_{O A B} = \frac{1}{2} . O A . O B . \sin (180^{o} - α); S_{O C D} = \frac{1}{2} . O D . O C . \sin (180^{o} - α) . \end{array}$

Mà $\sin (180^{o} - α) = \sin α$

$\Rightarrow S_{O A B} = \frac{1}{2} . O A . O B . \sin α; S_{O C D} = \frac{1}{2} . O D . O C . \sin α .$

$\begin{array}{l} \Rightarrow S_{A B C D} = (S_{O A D} + S_{O A B}) + (S_{O B C} + S_{O C D}) \\ = \frac{1}{2} . O A . \sin α . (O D + O B) + \frac{1}{2} . O C . \sin α . (O B + O D) \\ = \frac{1}{2} . O A . \sin α . B D + \frac{1}{2} . O C . \sin α . B D \\ = \frac{1}{2} . B D . \sin α . (O A + O C) \\ = \frac{1}{2} . A C . B D . \sin α = \frac{1}{2} . x . y . \sin α . \end{array}$

b) Nếu $A C ⊥ B D$ thì $α = 90^{o} \Rightarrow \sin α = 1.$

$\Rightarrow S_{A B C D} = \frac{1}{2} . x . y .1 = \frac{1}{2} . x . y .$

Lý thuyết Bài 2. Định lí cosin và định lí sin

1. Định lí cosin trong tam giác

Trong tam giác ABC:

$\begin{array}{l} a^{2} = b^{2} + c^{2} - 2 b c \cos A \\ b^{2} = c^{2} + a^{2} - 2 c a \cos B \\ c^{2} = a^{2} + b^{2} - 2 a b \cos C \end{array}$

Hệ quả

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

2. Định lí sin trong tam giác

Trong tam giác ABC: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R .$

(R là bán kính đường tròn ngoại tiếp tam giác ABC)

Hệ quả

$a = 2 R . \sin A; b = 2 R \sin B; c = 2 R \sin C$

$\sin A = \frac{a}{2 R}; \sin B = \frac{b}{2 R}; \sin C = \frac{c}{2 R} .$

3. Các công thức tính diện tích tam giác

1) $S = \frac{1}{2} a h_{a} = \frac{1}{2} b h_{b} = \frac{1}{2} c h_{c}$

2) $S = \frac{1}{2} b c \sin A = \frac{1}{2} c a \sin B = \frac{1}{2} a b \sin C$

3) $S = \frac{a b c}{4 R}$

4) $S = p r = \frac{(a + b + c) . r}{2}$

5) $S = \sqrt{p (p - a) (p - b) (p - c)}$ (Công thức Heron)

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

215

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

256

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

277

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

229