Toptailieu.vn xin giới thiệu 40 bài tập trắc nghiệm Giải hệ phương trình bằng phương cách lập hệ phương trình (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Giải hệ phương trình bằng phương cách lập hệ phương trình
Câu 1: Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số mới lớn hơn số đã cho là 63. Tổng của số đã cho và số mới tạo thành 99. Tổng các chữ số của số đó là?
A. 9
B. 8
C. 7
D. 6
Lời giải:
Gọi số cần tìm là
Đổi chỗ hai chữ số của nó thì ta được một số mới là
Ta có hệ phương trình:
Vậy số cần tìm là 18 nên tổng các chữ số là: 1 + 8 = 9
Đáp án cần chọn là: A
Câu 2: Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 18. Tổng của số đã cho và số mới tạo thành bằng 66. Tổng các chữ số của số đó là?
A. 9
B. 8
C. 7
D. 6
Lời giải:
Gọi số cần tìm là
Đổi chỗ hai chữ số của nó thì ta được một số mới là
Ta có hệ phương trình:
Vậy số cần tìm là 24 nên tổng các chữ số là 2 + 4 = 6
Đáp án cần chọn là: D
Câu 3: Cho một số có hai chữ số. Chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng 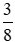
A. 12
B. 16
C. 14
D. 6
Lời giải:
Gọi số cần tìm là
Đổi chỗ hai chữ số của nó thì ta được một số mới là
Ta có hệ phương trình:
Vậy số cần tìm là 72 nên tích các chữ số là 2.7 = 14
Đáp án cần chọn là: C
Câu 4: Một ô tô đi quãng đường AB với vận tốc 50 km/h, rồi đi tiếp quãng đường BC với vận tốc 45 km/h. Biết quãng đường tổng cộng dài 165 km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên đoạn đường AB.
A. 2 giờ
B. 1,5 giờ
C. 1 giờ
D. 3 giờ
Lời giải:
Gọi thời gian ô tô đi trên mỗi đoạn đường AB và BC lần lượt là x, y
(x > 0; y > 0,5; đơn vị: giờ). Ta có hệ phương trình:
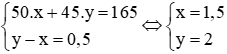
Vậy thời gian ô tô đi hết quãng đường AB là 1,5 giờ. Thời gian ô tô đi hết quãng đường BC là 2 giờ.
Đáp án cần chọn là: B
Câu 5: Một ô tô đi quãng đường AB với vận tốc 52 km/h, rồi đi tiếp quãng đường BC với vận tốc 42 km/h. Biết quãng đường tổng cộng dài 272 km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 2 giờ. Tính thời gian ô tô đi trên đoạn đường BC.
A. 2 giờ
B. 4 giờ
C. 1 giờ
D. 3 giờ
Lời giải:
Gọi thời gian ô tô đi trên mỗi đoạn đường AB và BC lần lượt là x, y
(x > 0; y > 2; đơn vị: giờ).
Quãng đường AB là 52x (km), quãng đường BC là 42 (km) mà tổng quãng đường 272 km nên ta có phương trình 52x + 42y = 272
Vì thời gian đi quãng đường AB ít hơn thời gian đi quãng đường BC là 2 giờ nên ta có phương trình y – x = 2
Vậy thời gian ô tô đi hết quãng đường AB là 2 giờ. Thời gian ô tô đi hết quãng đường BC là 4 giờ.
Đáp án cần chọn là: B
Câu 6. Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 3 giờ, còn nếu xe chạy chậm lại mỗi giờ 10 km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc ban đầu.
A. 40 km/h
B. 35 km/h
C. 50 km/h
D. 60 km/h
Lời giải:
Gọi vận tốc lúc đầu của xe là x (km/h; x > 10), thời gian theo dự định là y (y > 3) (giờ)
Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ nên ta có phương trình (x + 10) (y – 3) = xy
Vậy vận tốc ban đầu là 40 km/h
Đáp án cần chọn là: A
Câu 7: Một xe đạp dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 1 giờ, còn nếu xe chạy chậm lại mỗi giờ 5 km thì đến nơi chậm mất 2 giờ. Tính vận tốc của xe lúc ban đầu.
A. 8 km/h
B. 12 km/h
C. 10 km/h
D. 20 km/h
Lời giải:
Gọi vận tốc lúc đầu của xe là x (km/h; x > 10), thời gian theo dự định là y (y > 3) (giờ)
Quãng đường xe đi được là: x.y (km)
Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 1 giờ nên ta có phương trình (x + 10) (y – 1) = xy
Nếu xe chạy chậm lại mỗi giờ 5 km thì đến nơi chậm mất 2 giờ nên ta có phương trình (x – 5) (y + 2) = xy
Vậy vận tốc ban đầu là 10 km/h
Đáp án cần chọn là: C
Câu 8: Một cano chạy trên sông trong 7 giờ, xuôi dòng 108 km và ngược dòng 63 km. Một lần khác cũng trong 7 giờ, cano xuôi dòng 81 km và ngược dòng 84 km. Tính vận tốc nước chảy.
A. 4 km/h
B. 3 km/h
C. 2 km/h
D. 2,5 km/h
Lời giải:
Gọi vận tốc thực của cano là x (km/h, x > 0), vận tốc dòng nước là y (km/h, 0 < y < x)
Vận tốc cano khi xuôi dòng là x + y (km/h), vận tốc cano khi ngược dòng là: x – y (km/h)
Cano chạy trên sông trong 7 giờ, xuôi dòng 108 km và ngược dòng 63 km nên ta có phương trình:
Cano chạy trên sông trong 7 giờ, xuôi dòng 81 km và ngược dòng 84 km nên ta có phương trình:
Vậy vận tốc dòng ngước là 3 km/h
Đáp án cần chọn là: B
Câu 9: Một chiếc cano đi xuôi dòng theo một khúc sông trong 3 giờ và đi ngược dòng trong 4 giờ, được 380 km. Một lần khác cano này xuôi dòng trong 1 giờ và ngược dòng trong vòng 30 phút được 85 km. Hãy tính vận tốc của dòng nước (vận tốc thật của cano và vận tốc dòng nước ở hai lần là như nhau).
A. 5 km/h
B. 3 km/h
C. 2 km/h
D. 2,5 km/h
Lời giải:
Gọi vận tốc thực của cano là x (km/h, x > 0), vận tốc dòng nước là y (km/h, 0 < y < x)
Vận tốc cano khi xuôi dòng là x + y (km/h), vận tốc cano khi ngược dòng là: x – y (km/h)
Cano đi xuôi dòng theo một khúc sông trong 3 giờ và đi ngược dòng trong 4 giờ, được 380 km nên ta có phương trình: 3 (x + y) + 4 (x – y) = 380
Cano xuôi dòng trong 1 giờ và ngược dòng trong 30 phút được 85 km nên ta có phương trình:
Vậy vận tốc dòng ngước là 5 km/h
Đáp án cần chọn là: A
Câu 10: Hai người đi xe đạp xuất phát đồng thời từ hai thành phố cách nhau 38 km. Họ đi ngược chiều và gặp nhau sau 2 giờ. Hỏi vận tốc của người thứ nhất, biết rằng đến khi gặp nhau, người thứ nhất đi được nhiều hơn người thứ hai 2 km.
A. 7 km/h
B. 8 km/h
C. 9 km/h
D. 10 km/h
Lời giải:
Gọi vận tốc của người thứ nhất và người thứ hai lần lượt là x, y (km/h, x, y > 0)
Quãng đường người thứ nhất đi được khi gặp nhau là 2x (km)
Quãng đường người thứ hai đi được đến khi gặp nhau là 2y (km)
Ta có hệ phương trình 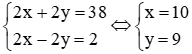
Vậy vận tốc của người thứ nhất là 10 (km/h)
Đáp án cần chọn là: D
Câu 11: Hai người đi xe máy xuất phát đồng thời từ hai thành phố cách nhau 225 km. Họ đi ngược chiều và gặp nhau sau 3 giờ. Hỏi vận tốc của người thứ nhất, biết rằng vận tốc người thứ nhất lớn hơn người thứ hai 5 km/h.
A. 40 km/h
B. 35 km/h
C. 45 km/h
D. 50 km/h
Lời giải:
Gọi vận tốc của người thứ nhất và người thứ hai lần lượt là x, y (km.h, x > 5, y > 0)
Quãng đường người thứ nhất đi được khi gặp nhau là 3x (km)
Quãng đường người thứ hai đi được đến khi gặp nhau là 3y (km)
Ta có hệ phương trình
Vậy vận tốc của người thứ nhất là 40 km/h
Đáp án cần chọn là: A
Câu 12: Một khách du lịch đi trên ô tô 4 giờ sau đó đi tiếp bằng tàu hỏa trong 7 giờ được quãng đường dài 640 km. Hỏi vận tốc của tàu hỏa biết mỗi giờ tàu hỏa đi nhanh hơn ô tô 5 km.
A. 40 km/h
B. 50 km/h
C. 60 km/h
D. 65 km/h
Lời giải:
Gọi vận tốc của tàu hỏa và ô tô lần lượt là x, y (km/h, x > y > 0; x > 5)
Vì khách du lịch đi ô tô 4 giờ sau đó đi tiếp bằng tàu hỏa trong 7 giờ được quãng đường dài 640 km nên ta có phương trình 7x + 4y = 640
Và mỗi giờ tàu hỏa đi nhanh hơn ô tô 5 km nên ta có phương trình x – y = 5
Suy ra hệ phương trình:
Vậy vận tốc tàu hỏa là 60km/h
Đáp án cần chọn là: C
Câu 13: Một khách du lịch đi trên ô tô 5 giờ sau đó đi tiếp bằng xe máy trong 3 giờ được quãng đường dài 330 km. Hỏi vận tốc của ô tô, biết rằng mỗi giờ xe máy đi chậm hơn ô tô 10 km.
A. 40 km/h
B. 50 km/h
C. 35 km/h
D. 45 km/h
Lời giải:
Gọi vận tốc của ô tô và xe máy lần lượt là x, y (km/h, x > y > 0; x > 10)
Vì khách du lịch đi trên ô tô 5 giờ, sau đó đi tiếp bằng xe máy trong 3 giờ được quãng đường dài 330 km nên ta có phương trình 5x + 3y = 330
Và mỗi giờ ô tô đi nhanh hơn xe máy 10 km nên ta có phương trình x – y = 10
Suy ra hệ phương trình:
Vậy vận tốc ô tô là 45 km/h
Đáp án cần chọn là: D
Câu 14: Hai vòi nước cùng chảy vào một bể thì sau 4 giờ 48 phút bể đầy. Nếu vòi I chảy riêng trong 4 giờ, vòi II chảy riêng trong 3 giờ thì cả hai vòi chảy được 3/4 bể. Tính thời gian vòi I chảy 1 mình đầy bể.
A. 6 giờ
B. 8 giờ
C. 10 giờ
D. 12 giờ
Lời giải:
Gọi thời gian vòi I, vòi II chảy một mình đầy bể lần lượt là x, y 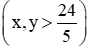
Mỗi giờ vòi I chảy được 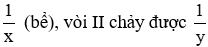
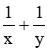
Vì hai vòi ngước cùng chảy vào một bể thì sau 4 giờ 48 phút 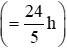
Nếu vòi I chảy riêng trong 4 giờ, vòi II chảy riêng trong 3 giờ thì cả hai vòi chảy được
Suy ra hệ phương trình:
Vậy thời gian vòi I một mình đầy bể là 8h.
Đáp án cần chọn là: B
Câu 15: Hai vòi ngước cùng chảy vào một bể không có nước thì sau 1,5 giờ sẽ đầy bể. Nếu mở vòi 1 chảy trong 0,25 giờ rồi khóa lại và mở vòi 2 chảy trong 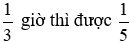
A. 2,5h
B. 2h
C. 3h
D. 4h
Lời giải:
Gọi thời gian vòi 1 chảy một mình đầy bể là x (h), thời gian vòi 2 chảy một mình đầy bể là y (h) (x; y > 1,5)
Mỗi giờ vòi I chảy được 
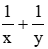
Hai vòi cùng chảy thì sau 1,5h sẽ đầy bể nên ta có phương trình:
Nếu mở vòi 1 chảy trong 0,25h rồi khóa lại và mở vòi 2 chảy trong 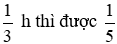
Từ (1) và (2) ta có hệ phương trình:
Vậy thời gian vòi 2 chảy một mình đầy bể là 2,5h
Đáp án cần chọn là: A
Câu 16: Hai bạn A và B cùng làm chung một công việc thì hoàn thành sau 6 ngày. Hỏi nếu A làm một nửa công việc rồi nghỉ thì B hoàn thành nốt công việc trong bao lâu? Biết rằng nếu làm một mình xong công việc thì B làm lâu hơn A là 9 ngày.
A. 9 ngày
B. 18 ngày
C. 10 ngày
D. 12 ngày
Lời giải:
Gọi thời gian A, B làm một mình xong công việc lần lượt là x, y (y > x > 6, đơn vị: ngày)
Mỗi ngày các bạn A, B lầm lượt làm được 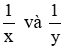
Vì hai bạn A và B cùng làm chung một công việc thì hoàn thành sau 6 ngày nên ta có:
Do làm một mình xong công việc thì B làm lâu hơn A là 9 ngày nên ta có phương trình: y – x = 9 (2)
Từ (1) và (2) ta có hệ phương trình:
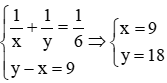
Vậy B hoàn thành cả công việc trong 18 ngày.
Suy ra sau khi A làm một mình xong nửa công việc rồi nghỉ, B hoàn thành công việc còn lại trong 9 ngày.
Đáp án cần chọn là: A
Câu 17: Hai bạn A và B cùng làm chung một công việc thì hoàn thành sau 8 ngày. Hỏi nếu A làm riêng hết 1/3 công việc rồi nghỉ thì B hoàn thành nốt công việc trong thời gian bao lâu? Biết rằng nếu làm một mình xong công việc thì A làm nhanh hơn B là 12 ngày.
A. 16 ngày
B. 18 ngày
C. 10 ngày
D. 12 ngày
Lời giải:
Gọi thời gian A, B làm một mình xong công việc lần lượt là x, y (y > x > 0; y > 12, đơn vị: ngày)
Mỗi ngày các bạn A, B lầm lượt làm được 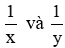
Vì hai bạn A và B cùng làm chung một công việc thì hoàn thành sau 8 ngày nên ta có:
Do làm một mình xong công việc thì B làm lâu hơn A là 12 ngày nên ta có phương trình: y – x = 12 (2)
Từ (1) và (2) ta có hệ phương trình
Vậy B hoàn thành cả công việc trong 24 ngày
Suy ra sau khi A làm một mình xong 1/3 công việc rồi nghỉ, B hoàn thành 2/3 công việc còn lại trong 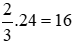
Đáp án cần chọn là: A
Câu 18: Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ. Trên thực tếm xí nghiệp 1 vượt mức 12%, xí nghiệp 2 vượt mức 10%, do đó cả hai xí nghiệp làm tổng cộng 400 dụng cụ. Tính số dụng cụ xí nghiệp 2 phải làm theo kế hoạch.
A. 160 dụng cụ
B. 200 dụng cụ
C. 120 dụng cụ
D. 240 dụng cụ
Lời giải:
Gọi số dụng cụ cần làm của xí nghiệp 1 và xí nghiệp 2 lần lượt là x, y
(x, y ∈ N*; x, y < 360, dụng cụ)
Số dụng cụ xí nghiệp 1 và xí nghiệp 2 làm được khi vượt mức lần lượt là 112%x và 110%y (dụng cụ)
Ta có hệ phương trình
Vậy xí nghiệp 1 phải làm 200 dụng cụ, xí nghiệp 2 phải làm 160 dụng cụ.
Đáp án cần chọn là: A
Câu 19: Tháng thứ nhất, 2 tổ sản xuất được 1200 sản phẩm. Tháng thứ hai, tổ 1 vượt mức 30% và tổ II bị giảm năng suất 22% so với tháng thứ nhất. Vì vậy 2 tổ đã sản xuất được 1300 sản phẩm. Hỏi tháng thứ hai, tổ 2 sản xuất được bao nhiêu sản phẩm.
A. 400 sản phẩm
B. 450 sản phẩm
C. 390 sản phẩm
D. 500 sản phẩm
Lời giải:
Gọi số sản phẩm của tổ I sản xuất được trong tháng thứ I là x (sản phẩm)
Số sản phẩm của tổ II sản xuất được trong tháng thứ nhất là y (sản phẩm) (x, y ∈ N*)
Tháng thứ nhất 2 tổ sản xuất được 1200 sản phẩm nên ta có phương trình:
x + y = 1200 (1)
Tháng thứ hai tổ I vượt mức 30% và tổ II giảm mức đi 22% so với tháng thứ nhất nên 2 tổ đã sản xuất được 1300 sản phẩm, ta có:
Từ (1) và (2) ta có hệ phương trình:
Vậy trong tháng thứ hai tổ II sản xuất được 500.78 : 100 = 390 sản phẩm
Đáp án cần chọn là: C
Câu 20: Một tam giác có chiều cao bằng 3/4 cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 4 dm thì diện tích của nó tăng thêm 12 dm2. Tính diện tích của tam giác ban đầu.
A. 700 dm2
B. 678 dm2
C. 627 dm2
D. 726 dm2
Lời giải:
Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a ∈ N*, a > 3, dm)
Diện tích tam giác ban đầu là 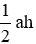
Vì chiều cao bằng 3/4 cạnh đáy nên ta có phương trình:
Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 dm2.
Vậy chiều cao của tam giác bằng 44 dm, cạnh đáy tam giác bằng 33 dm
Suy ra diện tích tam giác ban đầu là 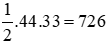
Đáp án cần chọn là: D
Câu 21: Một tấm bìa hình tam giác có chiều cao bằng 1/4 cạnh đáy tương ứng. Nếu tăng chiều cao 2 dm và giảm cạnh đáy 2 dm thì diện tích tam giác tăng thêm 2,5 dm2. Tính chiều cao và cạnh đáy của tấm bìa lúc đầu.
A. 1,5 dm và 6 dm
B. 2 dm và 8 dm
C. 1 dm và 4 dm
D. 3 dm và 12 dm
Lời giải:
Gọi chiều cao của tam giác là h, cạnh đáy tam giác là a. (h, a , dm); (a > 2)
Diện tích tam giác ban đầu là 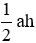
Vì chiều cao bằng 1/4 cạnh đáy nên ta có phương trình
Nếu chiều cao tăng thêm 2 dm và cạnh đáy giảm đi 2 dm thì diện tích của nó tăng thêm 2,5 dm2.
Vậy chiều cao và cạnh đáy của tấm bìa lần lượt là 1,5 dm và 6 dm
Đáp án cần chọn là: A
Câu 22: Một khu vườn hình chữ nhật có chu vi bằng 48 m. Nếu tăng chiều rộng lên bốn lần và tăng chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162m. Tìm diện tích của khu vườn ban đầu.
A. 24m2
B. 153m2
C. 135m2
D. 14m2
Lời giải:
Gọi chiều dài và chiều rộng của khu vương hình chữ nhật lần lượt là x, y
(24 > x > y > 0; m)
Vì khu vườn hình chữ nhật có chu vi bằng 48 m nên ta có (x + y). 2 = 48
Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162m
Nên ta có phương trình (4y + 3x). 2 = 162
Suy ra hệ phương trình 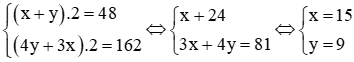
Vậy diện tích khu vườn ban đầu là 15.9 = 135m2
Đáp án cần chọn là: C
Câu 23: Một hình chữ nhật có chu vi 300cm. Nếu tăng chiều rộng thêm 5cm và giảm chiều dài 5 cm thì diện tích tăng 275 cm2. Tính chiều dài và chiều rộng của hình chữ nhật.
A. 120 cm và 30 cm
B. 105 cm và 45 cm
C. 70 cm và 80 cm
D. 90 cm và 60 cm
b
Gọi chiều dài và chiều rộng của khu vương hình chữ nhật lần lượt là x, y
(150 > x > y > 0; cm)
Diện tích ban đầu của khu vương là x.y (cm2)
Vì hình chữ nhật có chu vi bằng 300 (cm) nên ta có (x + y). 2 = 300
Nếu tăng chiều rộng thêm 5 cm và giảm chiều dài 5cm thì diện tích tăng 275cm2
Nên ta có phương trình (x − 5).(y + 5) = xy + 275
Vậy chiều rộng của hình chữ nhật ban đầu là 45 cm
Chiều dài của hình chữ nhật ban đầu là 105 cm
Đáp án cần chọn là: B
Câu 24: Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng 4/5 số sách ở giá thứ nhất. Tính số sách trên giá thứ hai.
A. 150 cuốn
B. 300 cuốn
C. 200 cuốn
D. 250 cuốn
Lời giải:
Gọi số sách trên hai giá lần lượt là x, y (0 < x, y < 450, cuốn)
Vì hai giá sách có 450 cuốn nên ta có phương trình: x + y = 450 (cuốn)
Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng 4/5 số sách ở giá thứ nhất nên ta có:
Vậy số sách trên giá thứ nhất là 300 cuốn, số sách trên giá thứ hai là 150 cuốn.
Đáp án cần chọn là: A
Câu 25: Nam có 360 viên bi trong hai hộp. Nếu Nam chuyển 30 viên bi từ hộp thứ hai sang hộp thứ nhất thì số viên vi ở hộp thứ nhất bằng 5/7 số viên bi ở hộp thứ hai. Hỏi hộp thứ hai có bao nhiêu viên bi?
A. 250 viên
B. 180 viên
C. 120 viên
D. 240 viên
Lời giải:
Gọi số viên bi trong hộp thứ nhất và hộp thứ hai lần lượt là x, y (0 < x, y < 360, viên)
Vì Nam có 360 viên bi nên ta có phương trình x + y = 360 (viên bi)
Nếu Nam chuyển 30 viên bi từ hộp thứ hai sang hộp thứ nhất thì số viên bi ở hộp thứ nhất bằng 5/7 số viên bi ở hộp thứ hai nên ta có phương trình
Vậy số viên bi ở hộp thứ nhất là 120 viên bi, số viên bi ở hộp thứ hai là 240 viên bi.
Đáp án cần chọn là: D
Câu 26: Trên một cánh đồng cấy 60 ha lúa giống mới và 40 ga lúa giống cũ, thu hoạch được tất cả 460 tấn thóc. Hỏi năng suất lúa mới trên 1 ha là bao nhiêu, biết rằng 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn.
A. 5 tấn
B. 4 tấn
C. 6 tấn
D. 3 tấn
Lời giải:
Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị: tấn/ha
Vì cấy 60 ha lúa giống mới và 40 ga lúa giống cũ, thu hoạch được tất cả 460 tấn thóc nên ta có 60x + 40y = 460
Vì 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn nên ta có phương trình: 4y – 3x = 1
Vậy năng suất lúa mới trên 1 ha là 5 tấn
Đáp án cần chọn là: A
Câu 27: Trên một cánh đồng cấy 50 ha lúa giống mới và 30 ha lúa giống cũ, thu hoạch được tất cả 410 tấn thóc. Hỏi năng suất lúa cũ trên 1 ha là bao nhiêu, biết rằng 5 ha trồng lúa mới thu hoạch được nhiều hơn 6 ha trồng lúa cũ là 0,5 tấn.
A. 5,5 tấn
B. 4 tấn
C. 4,5 tấn
D. 3 tấn
Lời giải:
Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị: tấn/ha
Vì đồng cấy 50 ha lúa giống mới và 30 ha lúa giống cũ, thu hoạch được tất cả 410 tấn thóc nên ta có 50x + 30y = 410
Vì 5 ha trồng lúa mới thu hoạch được nhiều hơn 6 ha trồng lúa cũ là 0,5 tấn nên ta có phương trình: 5x – 6y = 0,5
Vậy năng suất lúa cũ trên 1 ha là 4,5 tấn.
Đáp án cần chọn là: C
Câu 28: Trong một kì thi, hai trường A, B có tổng cộng 350 học sinh dự thi. Kết quả hai trường đó có 338 học sinh trúng tuyển. Tính ra thì trường A có 97% và trường B có 96% số học sinh trúng tuyển. Hỏi trường B có bao nhiêu học sinh dự thi.
A. 200 học sinh
B. 150 học sinh
C. 250 học sinh
D. 225 học sinh
Lời giải:
Gọi số học sinh dự thi của hai trường A, B lần lượt là x, y (350 > x, y > 0) (học sinh)
Vì hai trường A, B có tổng cộng 350 học sinh dự thi nên ta có phương trình
x + y = 350 (học sinh)
Vì trường A có 97% và trường B có 96% số học sinh trúng tuyển và cả hai trường đó có 338 học sinh trúng tuyển nên ta có phương trình 97%.x +96%.y = 338
Vậy trường B có 150 học sinh dự thi
Đáp án cần chọn là: B
Câu 29: Hai trường có tất cả 300 học sinh tham gia một cuộc thi. Biết trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt. Số học sinh dự thi của trường A và trường B lần lượt là:
A. 160 và 140
B. 200 và 100
C. 180 và 120
D. Tất cả đều sau
Lời giải:
Gọi số học sinh của trường thứ nhất dự thi là x (học sinh) (x ∈ N*, x < 300)
Số học sinh của trường thứ hai dự thi là y (học sinh) (y ∈ N*, y < 300)
Hai trường có tất cả 300 học sinh tham gia cuộc thi nên ta có phương trình: x + y = 300 (1)
Trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt, ta có:
Vậy số học sinh của trường thứ nhất dự thi là 180 học sinh; Số học sinh của trường thứ hai dự thi là 120 học sinh.
Đáp án cần chọn là: C
Câu 30: Một mảnh đất hình chữ nhật có chu vi bằng 42m. Đường chéo hình chữ nhật dài 15m. Tính độ dài chiều rộng mảnh đất hình chữ nhật.
A. 10m
B. 12m
C. 9m
D. 8m
Lời giải:
Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y
(21 > x > y > 0; m)
Vì mảnh đất hình chữ nhật có chu vi bằng 42m nên ta có (x + y). 2 = 42
Đường chéo hình chữ nhật dài 15m nên ta có phương trình: x2 + y2 = 152
Vậy chiều rộng mảnh đất ban đầu là 9m
Đáp án cần chọn là: C
Câu 31: Một mảnh đất hình chữ nhật có nửa chu vi bằng 34 m. Đường chéo hình chữ nhật dài 26 m. Tính chiều dài mảnh đất hình chữ nhật.
A. 24m
B. 12m
C. 18m
D. 20m
Lời giải:
Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y
(34 > x > y > 0; m)
Vì mảnh đất hình chữ nhật có nửa chu vi bằng 37m nên ta có x + y = 37
Đường chéo hình chữ nhật dài 26m nên ta có phương trình: x2 + y2 = 262
Vậy chiều dài mảnh đất ban đầu là 24m
Đáp án cần chọn là: A
Câu 32. Trong tháng đầu hai tổ sản xuất được 800 sản phẩm. Sang tháng thứ 2, tổ 1 sản xuất vượt mức 12%, tổ 2 giảm 10% so với tháng đầu nên cả hai tổ làm được 786 sản phẩm. Tính số sản phẩm tổ 1 làm được trong tháng đầu.
A. 500 sản phẩm
B. 300 sản phẩm
C. 200 sản phẩm
D. 400 sản phẩm
Lời giải:
Gọi số sản phẩm tổ 1 và tổ 2 làm được trong tháng đầu lần lượt là
x, y (x, y , x, y < 800 sản phẩm)
Số sản phẩm tổ 1 và tổ 2 làm được trong tháng hai là 112%.x và 90%.y sản phẩm
Ta có hệ phương trình:
Vậy số sản phẩm tổ 1 làm được trong tháng đầu là 300 sản phẩm.
Đáp án cần chọn là:B
Câu 33: Tổng hai số tự nhiên bằng 51. Biết số thứ nhất bằng số thứ hai. Tìm hai số tự nhiên đó.
A. 14 và 37
B. 36 và 15
C. 34 và 17
Lời giải:

Đáp án cần chọn là:B
Câu 34: Tìm hai số tự nhiên, biết tổng của chúng bằng 72 và nếu lấy số lớn chia số nhỏ thì được thương là 4 và số dư là 2.
Nếu gọi số nhỏ là x, số lớn là y (điều kiện và x < y) thì hệ phương trình ta lập được là:
A.
B.
C.
D.
Lời giải:

Đáp án cần chọn là:C
Câu 35: Tổng của hai số bằng 59. Hai lần số này bé hơn ba lần số kia là 7. Tích của hai số là:
A. 850
B. 800
C. 900
D. 750
Lời giải:

Đáp án cần chọn là:A
Câu 36: Có 50 con gà và chó. Biết tổng số chân gà và chó là 140 chân. An nói: ''Số gà nhiều hơn số chó'' đúng hay sai?
A. Đúng
B. Sai
Lời giải:

Đáp án cần chọn là:A
Câu 37: Hai người cùng làm một công việc trong 7h 12 phút thì xong công việc nếu người thứ 1 làm trong 4h người thứ hai làm trong 3h thì được 50% công việc. Hỏi mỗi người làm 1 mình trong mấy ngày thì xong
A. x = 12, y =18
B. x=18, y = 12
C. x = 11; y = 17
D. x = 20; y = 30
Lời giải:
Gọi thời gian người thứ 1 làm 1 mình xong công việc là x h đ/k x > 0 gọi thời gian người thứ 2 làm 1 mình xong công việc là y h đ/k y > 0
Trong 1 giờ cả 2 người làm được là 1/x + 1/y = 5/36
Trong 4h người thứ 1 và trong 3h người thứ 2 làm được là 4/x + 3/y = 1/2
Ta có hệ phương trình:
==> x = 12, y = 18
Đáp án cần chọn là:A
Câu 38: Năm ngoái, cả 2 cánh đồng thu hoạch được 500 tấn thóc. Năm nay, do áp dụng khoa học kĩ thuật nên lượng lúa thu được trên cánh đồng thứ nhất tăng lên 30% so với năm ngoái, trên cánh đồng thứ hai tăng 20%. Do đó tổng cộng cả hai cánh đồng thu được 630 tấn thóc. Hỏi trên mỗi cánh đồng năm nay thu được bao nhiêu tấn thóc?
A. 400 tấn và 230 tấn
B. 390 tấn và 240 tấn
C. 380 tấn và 250 tấn
D. Tất cả đều sai
Lời giải:
Gọi số thóc năm ngoái thu được của cánh đồng thứ nhất là (x) (tấn) (x > 0)
Gọi số thóc năm ngoái thu được của cánh đồng thứ hai là y (tấn) (y > 0)
Năm ngoái, cả 2 cánh đồng thu hoạch được 500 tấn thóc nên ta có phương trình:
x + y = 500 (1)
Năm nay, lượng lúa thu được trên cánh đồng thứ nhất tăng lên 30% so với năm ngoái, trên cánh đồng thứ hai tăng 20% nên ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
Vậy lượng lúa thu hoạch được năm nay của
cánh đồng thứ nhất là 300.1,3 = 390 (tấn);
lượng lúa thu được năm nay của
cánh đồng thứ hai là 200.1,2 = 240 tấn.
Đáp án cần chọn là:B
Câu 39: Một cano chạy trên sông trong 7 giờ, xuôi dòng 108 km và ngược dòng 63 km. Một lần khác cũng trong 7 giờ, cano xuôi dòng 81 km và ngược dòng 84 km. Tính vận tốc nước chảy
A. 4 km/h
B. 3 km/h
C. 2 km/h
D. 2,5 km/h
Lời giải:
Gọi vận tốc thực của cano là x (km/h, x > 0), vận tốc dòng nước là y (km/h, 0 < y < x)
Vận tốc cano khi xuôi dòng là x + y (km/h), vận tốc cano khi ngược dòng là: x – y (km/h)
Cano chạy trên sông trong 7 giờ, xuôi dòng 108 km và ngược dòng 63 km nên ta có phương trình
Cano chạy trên sông trong 7 giờ, xuôi dòng 81 km và ngược dòng 84 km nên ta có phương trình:
Ta có hệ phương trình:
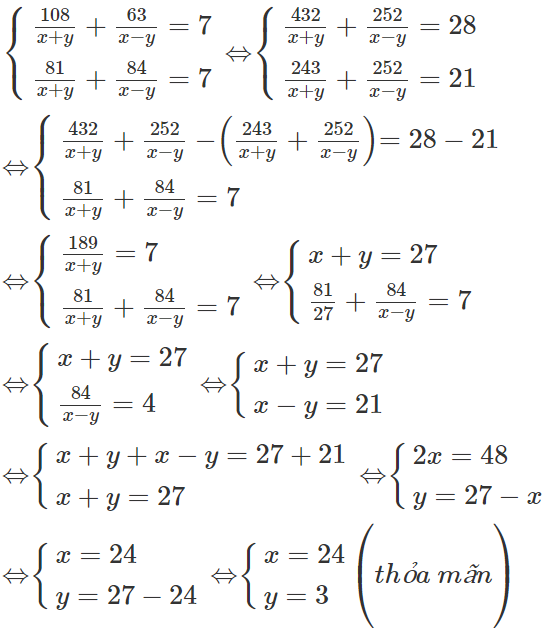
Đáp án cần chọn là:B
Câu 40: Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì họ làm được một phần tư công việc. Hỏi mỗi người thợ làm một mình thì trong bao nhiêu giờ mới xong công việc đó.
A. 24 giờ và 48 giờ
B. 24 giờ và 36 giờ
C. 36 giờ và 40 giờ
D. Đáp án khác
Lời giải:
Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)
Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)
Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc
Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc
Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc
Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc
Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 ta có phương trình:
Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:
Từ đó ta có hệ phương trình:
Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)
Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ
Đáp án cần chọn là:A
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.