Toptailieu.vn xin giới thiệu 35 bài tập trắc nghiệm Phương trình bậc hai một ẩn (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Phương trình bậc hai một ẩn
Câu 1: Phương trình nào dưới đây là phương trình bậc hai một ẩn
Lời giải:
Phương trình bậc hai một ẩn (hay gọi tắt là phương trình bậc hai) là phương trình có dạng ax2 + bx + c = 0 (a ≠ 0) trong đó a, b, c là các số thực cho trước, x là ẩn số.
Đáp án cần chọn là: B
Câu 2: Có bao nhiêu phương trình trong các phương trình dưới đây là phương trình bậc hai một ẩn:
A. 2
B. 3
C. 4
D. 0
Lời giải:
- Phương trình 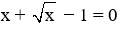
- Phương trình 2x + 2y2 + 3 = 9 có chứa hai biến x; y nên không là phương trình bậc hai một ẩn.
- Phương trình 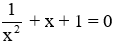
- Phương trình 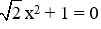
Vậy có hai phương trình bậc hai một ẩn trong số các phương trình đã cho.
Đáp án cần chọn là: A
Câu 3: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ = b2 – 4ac. Phương trình đã cho vô nghiệm khi:
A. ∆ < 0
B. ∆ = 0
C. ∆ ≥ 0
D. ∆ ≤ 0
Lời giải:
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu ∆ < 0 thì phương trình vô nghiệm
TH2. Nếu ∆ = 0 thì phương trình có nghiệm kép
TH3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: A
Câu 4: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ = b2 – 4ac > 0, khi đó, phương trình đã cho:
A. Vô nghiệm
B. Có nghiệm kép
C. Có hai nghiệm phân biệt
D. Có 1 nghiệm
Lời giải:
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu ∆ < 0 thì phương trình vô nghiệm
TH2. Nếu ∆ = 0 thì phương trình có nghiệm kép
TH3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: C
Câu 5: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ = b2 – 4ac > 0, khi đó, phương trình có hai nghiệm là:
Lời giải:
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b2 – 4ac
TH1: Nếu ∆ < 0 thì phương trình vô nghiệm
TH2. Nếu ∆ = 0 thì phương trình có nghiệm kép
TH3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: C
Câu 6: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức = b2 – 4ac = 0. Khi đó, phương trình có hai nghiệm là:
Lời giải:
Xét phương trình bậc hai một ẩn ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu ∆ < 0 thì phương trình vô nghiệm
TH2. Nếu ∆ = 0 thì phương trình có nghiệm kép
TH3: Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: D
Câu 7: Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6x2 – 7x = 0
Lời giải:
Đáp án cần chọn là: B
Câu 8: Không dùng công thức nghiệm, tính tích các nghiệm của phương trình 3x2 – 10x + 3 = 0
Lời giải:
Nên tích các nghiệm của phương trình là
Đáp án cần chọn là: C
Câu 9: Không dùng công thức nghiệm, tìm số nghiệm của phương trình −4x2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Lời giải:
Đáp án cần chọn là: D
Câu 10: Không dùng công thức nghiệm, tìm số nghiệm của phương trình
−9x2 + 30x − 25 = 0
A. 0
B. 1
C. 3
D. 2
Lời giải:
Đáp án cần chọn là: B
Câu 11: Tìm tích các giá trị của m để phương trình 4mx2 − x – 14m2 = 0 có nghiệm x = 2
Lời giải:
Thay x = 2 vào phương trình 4mx2 – x – 10m2 = 0, ta có:
Đáp án cần chọn là: A
Câu 12: Tìm tổng các giá trị của m để phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0 có nghiệm x = −3
A. −5
B. −4
C. 4
D. 6
Lời giải:
Thay x = −3 vào phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B
Câu 13: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: 9x2 − 15x + 3 = 0
A. ∆ = 117 và phương trình có nghiệm kép
B. ∆ = − 117 và phương trình vô nghiệm
C. ∆ = 117 và phương trình có hai nghiệm phân biệt
D. ∆ = − 117 và phương trình có hai nghiệm phân biệt
Lời giải:
Ta có: 9x2 − 15x + 3 = 0 (a = 9; b = −15; c = 3)
⇒ ∆ = b2 – 4ac = (−15)2 – 4.9.3 = 117 > 0 nên phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: C
Câu 14: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: −13x2 + 22x − 13 = 0
A. ∆ = 654 và phương trình có nghiệm kép
B. ∆ = −192 và phương trình vô nghiệm
C. ∆ = − 654 và phương trình vô nghiệm
D. ∆ = − 654 và phương trình có hai nghiệm phân biệt
Lời giải:
Ta có:
−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)
⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0 nên phương trình vô nghiệm
Đáp án cần chọn là: B
Câu 15: Tính biệt thức ∆ từ đó tìm các nghiệm (nếu có) của phương trình
A. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = √2
B. ∆ < 0 và phương trình vô nghiệm
C. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = −√2
D. ∆ > 0 và phương trình có hai nghiệm phân biệt x1 = −√2 ; x2 =√2
Lời giải:
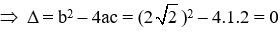
Đáp án cần chọn là: A
Câu 16: Tính biệt thức ∆ từ đó tìm các nghiệm (nếu có) của phương trình
A. ∆ > 0 và phương trình có nghiệm kép
B. ∆ < 0 và phương trình vô nghiệm
C. ∆ = 0 và phương trình có nghiệm kép
D. ∆ > 0 và phương trình có hai nghiệm phân biệt
Lời giải:
Đáp án cần chọn là: D
Câu 17: Tìm điều kiện cùa tham số m để phương trình −x2 + 2mx – m2 − m = 0 có hai nghiệm phân biệt
A. m ≥ 0
B. m = 0
C. m > 0
D. m < 0
Lời giải:
Phương trình −x2 + 2mx – m2 − m = 0 (a = −1; b = 2m; c = − m2 – m)
⇒ ∆ = (2m)2 – 4. (−1).( − m2 – m) = 4m2 – 4m2 – 4m = − 4
Để phương trình đã cho có hai nghiệm phân biệt thì
Vậy với m < 0 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: D
Câu 18: Tìm điều kiện cùa tham số m để phương trình x2 – 2(m – 2)x + m2 − 3m + 5 = 0 có hai nghiệm phân biệt
A. m < −1
B. m = −1
C. m > −1
D. m −1
Lời giải:
Phương trình x2 – 2(m – 2)x + m2 − 3m + 5 = 0
(a = 1; b = – 2(m – 2); c = m2 − 3m + 5)
⇒ ∆ = [– 2(m – 2)]2 – 4.1.( m2 − 3m + 5) = 4m2 − 16m + 16 − 4m2 + 12m – 20
= − 4m – 4
Để phương trình đã cho có hai nghiệm phân biệt thì:
Vậy với m < −1 thì phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: A
Câu 19: Tìm các giá trị của tham số m để phương trình x2 + mx − m = 0 có nghiệm kép.
A. m = 0; m = −4
B. m = 0
C. m = −4
D. m = 0; m = 4
Lời giải:
Phương trình x2 + mx − m = 0 (a = 1; b = m; c = −m)
⇒ ∆ = m2 – 4.1.(−m) = m2 + 4m
Để phương trình đã cho có nghiệm kép thì
Vậy với m = 0; m = −4 thì phương trình có nghiệm kép.
Đáp án cần chọn là: A
Câu 20: Tìm các giá trị của tham số m để phương trình x2 + (3 – m)x – m + 6 = 0 có nghiệm kép.
A. m = 3; m = −5
B. m = −3
C. m = 5; m = −3
D. m = 5
Lời giải:
Phương trình x2 + (3 – m)x – m + 6 = 0 (a = 1; b = 3 – m; c = −m + 6)
⇒ ∆ = (3 – m)2 – 4.1.( −m + 6) = m2 – 6m + 9 + 4m – 24 = m2 – 2m – 15
Để phương trình đã cho có nghiệm kép thì
Phương trình (*) có ∆m = (−2)2 – 4.1.(−15) = 64 > 0 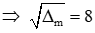
Vậy với m = 5; m = −3 thì phương trình có nghiệm kép.
Đáp án cần chọn là: C
Câu 21: Hệ số c của phương trình x2 + 7x + 9 = 9 là?
A. 9
B. -9
C. 0
D. 18
Lời giải:
Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 .Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0 .
Khi đó ta có:
Do đó hệ số c là x2 + 7x + 9 = 9 ⇔ x2 + 7x = 0
Đáp án cần chọn là:C
Câu 22: Trong các phương trình sau, phương trình nào là phương trình bậc hai?
A. x2 + 4x - 7 = x2 + 8x - 10
B. x3 + 8x = 0
C. x2 - 4 = 0
D. 5x - 1 = 0
Lời giải:
Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 .Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0 .
+ x2 + 4x - 7 = x2 + 8x - 10 ⇔ 4x - 3 = 0 . Loại vì đây là phương trình bậc nhất
+ x3 + 8x = 0 vì mũ cao nhất của x là 3 nên không là phương trình bậc hai.
+ x2 - 4 = 0 là phương trình bậc hai thỏa mãn
+ 5x - 1 = 0 là phương trình bậc nhất một ẩn
Đáp án cần chọn là:
Câu 23: Số nghiệm của phương trình x2 = 20x - 102 là?
A. 1 nghiệm
B. 2 nghiệm
C. Vô số nghiệm
D. Vô nghiệm
Lời giải:
Ta có:
Vậy phương tình đã cho có 1 nghiệm
Đáp án cần chọn là:A
Câu 24: Tập nghiệm của bất phương trình
A. x > -4
B. x < -4
C. x ≤ -4
D. x = -4
Lời giải:
Ta có:
Suy ra x = -4
Đáp án cần chọn là:D
Câu 25: Tập nghiệm của bất phương trình x2 + 10x + 26 < 1
A. x ≥ -5
B. x ≤ -5
C. x = -5
D. Vô nghiệm
Lời giải:
Ta có:
Bất phương trình vô nghiệm vì
Đáp án cần chọn là:D
Câu 26: Cho phương trình 2x2 – 10x + 100 = -2x + 10. Sau khi đưa phương trình trên về dạng ax2 + bx + c = 0 thì hệ số b là?
A. -8
B. -12
C. 12
D. 8
Lời giải:
Ta có:
2x2 – 10x + 100 = -2x + 10
⇔ 2x2 – 10x +100 + 2x -10 =0
⇔ 2x2 – 8x + 90 = 0
Đây là phương trình bậc hai một ẩn có a = 2; b = - 8 và c = 90 .
Đáp án cần chọn là:A
Câu 27: Cho phương trình 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10. Sau khi biến đổi đưa phương trình trên về dạng ax2 + bx+ c =0 thì hệ số a bằng ?
A. 2
B.1
C. 3
D. -1
Lời giải:
Ta có : 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10
⇔ 2x3 + 2x2 - 3x + 10 - 2x3 - x2 + 10= 0
⇔ x2 – 3x + 20 = 0
Phương trình trên là phương trình bậc hai một ẩn với a = 1; b = -3 và c = 20.
Đáp án cần chọn là:B
Câu 28: Giải phương trình -10x2 + 40 = 0
A. Vô nghiệm
B. x = 2
C. x = 4
D. x = ±2
Lời giải:
Ta có: -10x2 + 40 = 0
⇔ -10x2 = - 40 ⇔ x 2 = 4
⇔ x = ±2
Đáp án cần chọn là:C
Câu 29: Tìm tích các giá trị của m để phương trình 4mx2 − x – 14m2 = 0 có nghiệm x = 2
Lời giải:
Thay x = 2 vào phương trình 4mx2 – x – 10m2 = 0, ta có:
Đáp án cần chọn là:A
Câu 30: Tìm tổng các giá trị của m để phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0 có nghiệm x = −3
A. −5
B. −4
C. 4
D. 6
Lời giải:
Thay x = −3 vào phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là:B
Câu 31: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: 9x2 − 15x + 3 = 0
A. ∆ = 117 và phương trình có nghiệm kép
B. ∆ = − 117 và phương trình vô nghiệm
C. ∆ = 117 và phương trình có hai nghiệm phân biệt
D. ∆ = − 117 và phương trình có hai nghiệm phân biệt
Lời giải:
Ta có: 9x2 − 15x + 3 = 0 (a = 9; b = −15; c = 3)
⇒ ∆ = b2 – 4ac = (−15)2 – 4.9.3 = 117 > 0 nên phương trình có hai nghiệm phân biệt
Đáp án cần chọn là:C
Câu 32: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: −13x2 + 22x − 13 = 0
A. ∆ = 654 và phương trình có nghiệm kép
B. ∆ = −192 và phương trình vô nghiệm
C. ∆ = − 654 và phương trình vô nghiệm
D. ∆ = − 654 và phương trình có hai nghiệm phân biệt
Lời giải:
Ta có:
−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)
⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0 nên phương trình vô nghiệm
Đáp án cần chọn là:B
Câu 33: Tính biệt thức ∆ từ đó tìm các nghiệm (nếu có) của phương trình
A. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = √2
B. ∆ < 0 và phương trình vô nghiệm
C. ∆ = 0 và phương trình có nghiệm kép x1 = x2 = −√2
D. ∆ > 0 và phương trình có hai nghiệm phân biệt x1 = −√2 ; x2 =√2
Lời giải:
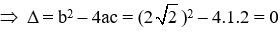
Đáp án cần chọn là:A
Câu 34: Phương trình x2 + x + 1/4 = 0 có một nghiệm là:
A. -1
B -1/2
C. 1/2
D. 2
Lời giải:
Ta có: Δ = 1 - 4.1/4 = 0. Khi đó phương trình có nghiệm kép x= -1/2
Đáp án cần chọn là:B
Câu 35: Cho phương trình 2x2 + x - 1 = 0 có tập nghiệm là:
A. {-1}
B. {-1; -1/2}
C. {-1; 1/2}
D. ∅
Lời giải:
ta có Δ = 1 - 4.2.(-1) = 9 => √%Delta; = 3
Khi đó phương trình có 2 nghiệm là
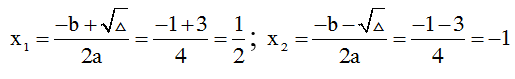
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.