Toptailieu.vn xin giới thiệu 35 câu trắc nghiệm Nhân đơn thức với đa thức (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 8 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

35 câu trắc nghiệm Nhân đơn thức với đa thức (có đáp án) chọn lọc

Bài 1: Tích 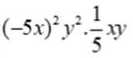  bằng

A. 5x³y³      

B. -5x³y³     

C. -x³y³       

D. x³y²

Lời giải

Ta có: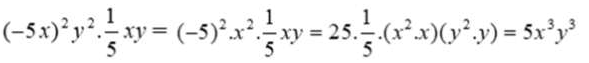 

Đáp án cần chọn là: A

Bài 2: Tích 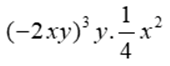 bằng

A. -2x⁴y⁵    

B.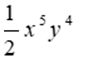   

C. 2x⁵y⁴      

D. -2x⁵y⁴

Lời giải

Ta có:

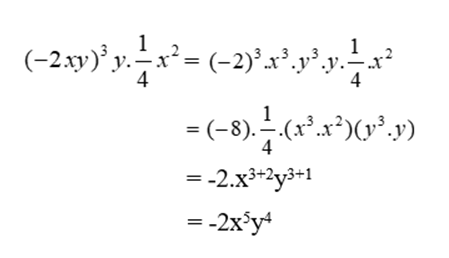
Đáp án cần chọn là: D

Bài 3: Thu gọn 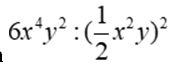,ta được

A. 12          

B. 24          

C. 24x²y     

D. 12x²y

Lời giải

Ta có:

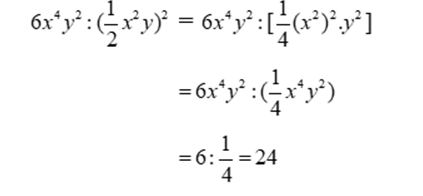
Đáp án cần chọn là: B

Bài 4: Thu gọn biểu thức 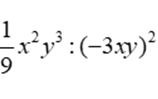 ta được

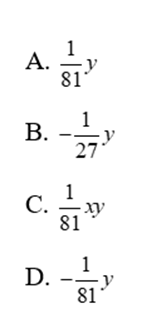
Lời giải

Ta có:

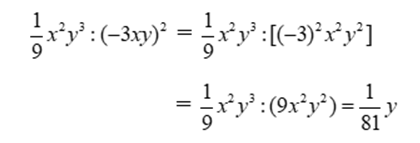
Đáp án cần chọn là: A

Bài 5: Kết quả của phép tính (ax² + bx – c).2a²x bằng

A. 2a⁴x³ + 2a²bx² – 2a²cx         

B. 2a³x³ + bx – c

C. 2a⁴x² + 2a²bx² – a²cx           

D. 2a³x³ + 2a²bx² – 2a²cx

Lời giải

Ta có: (ax² + bx – c).2a²x = 2a²x.(ax² + bx – c)

                                      = 2a²x.ax² + 2a²x.bx – 2a²x.c

                                      = 2a³x³ + 2a²bx² – 2a²cx

Đáp án cần chọn là: D

Bài 6: Tích 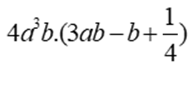 có kết quả bằng

A. 12a⁴b² – 4a³b + a³b             

B. 12a⁴b² – 4a³b² + a³b

C. 12a³b² + 4a³b² + 4a³b          

D. 12a⁴b² – 4a³b² + a³b

Lời giải

Ta có: 12a⁴b² – 4a³b + a³b = 4a³b.3ab – 4a³b.b + 4a³b.

                                      = 12a⁴b² – 4a³b² + a³b

Đáp án cần chọn là: D

Bài 7: Kết quả của phép tính -4x²(6x³ + 5x² – 3x + 1) bằng

A. 24x⁵ + 20x⁴ + 12x³ – 4x²     

B. -24x⁵ – 20x⁴ + 12x³ + 1

C. -24x⁵ – 20x⁴ + 12x³ – 4x²     

D. -24x⁵ – 20x⁴ – 12x³ + 4x²

Lời giải

Ta có: -4x²(6x³ + 5x² – 3x + 1)

= (-4x²).6x³ + (-4x²).5x² + (-4x²).(-3x) + (-4x²).1

= -24x⁵ – 20x⁴ + 12x³ – 4x²

Đáp án cần chọn là: C

Bài 8: Tích ( x- y)(x + y) có kết quả bằng

A. x² – 2xy + y²    

B. x² + y²    

C. x² – y²    

D. x² + 2xy + y²

Lời giải

Ta có ( x- y)(x + y) = x.x + x.y – x.y – y.y = x² – y²

Đáp án cần chọn là: C

Bài 9: Tích (2x – 3)(2x + 3) có kết quả bằng

A. 4x² + 12x+ 9    

B. 4x² – 9   

C. 2x² – 3   

D. 4x² + 9

Lời giải

Ta có (2x – 3)(2x + 3) = 2x.2x + 2x.3 – 3.2x + (-3).3

          = 4x² + 6x – 6x – 9 = 4x² – 9

Đáp án cần chọn là: B

Bài 10: Giá trị của biểu thức P = -2x²y(xy + y²) tại x = -1; y = 2 là

A. 8                     

B. -8           

C. 6            

D. -6

Lời giải

Thay x = -1; y = 2 vào biểu thức P = -2x²y(xy + y²) ta được

P = -2.(-1)².2[(-1).2 + 2²] = -4.2 = -8

Đáp án cần chọn là: B

Bài 11: Chọn câu sai.

A. Giá trị của biểu thức ax(ax + y) tại x = 1; y = 0 là a².

B. Giá trị của biểu thức ay²(ax + y) tại x = 0; y = 1 là (1 + a)².

C. Giá trị của biểu thức -xy(x - y) tại x = -5; y = -5 là 0.

D. Giá trị của biểu thức xy(-x - y) tại x = 5; y = -5 là 0.

Lời giải

+) Thay x = 1; y = 0 vào biểu thức ax(ax + y) ta được 

a.1(a.1+0) = a.a = a² nên phương án A đúng

+) Thay x = 0, y = 1 vào biểu thức ay²(ax + y) ta được 

a.1²(a.0+1) = a.1 = a nên phương án B sai.

+) Thay x = −5, y = −5 vào biểu thức −xy(x − y) ta được 

−(−5)(−5)[−5−(−5)] = −25.0 = 0  nên phương án C đúng

+) Thay x = 5, y = −5 vào biểu thức xy(−x − y) ta được 

5.(−5)[−5−(−5)] = −25.0 = 0 nên phương án D đúng.

Đáp án cần chọn là: B

Bài 12: Rút gọn và tính giá trị của biểu thức

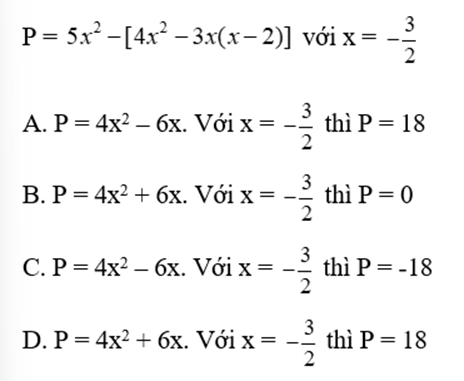
Lời giải

Ta có P = 5x² - [4x² - 3x(x - 2)]

= 5x² – (4x² – 3x² + 6x) = 5x² – (x² + 6x)

= 5x² – x² – 6x = 4x² – 6x

Thay 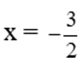 vào biểu thức P = 4x² – 6x ta được:

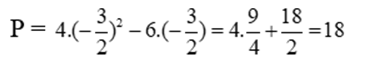
Vậy P = 4x² – 6x. Với 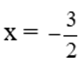 thì P = 18

Đáp án cần chọn là: A

Bài 13: Chọn câu đúng.

A. (x² – 1)(x² + 2x) = x⁴ – x³ – 2x      

B. (x² – 1)(x² + 2x) = x⁴ – x² – 2x

C. (x² – 1)(x² + 2x) = x⁴ + 2x³ – x² – 2x

D. (x² – 1)(x² + 2x) = x⁴ + 2x³ – 2x

Lời giải

Ta có: (x² – 1)(x² + 2x) = x².x² + x².2x – 1.x² – 1.2x

                                      = x⁴ + 2x³ – x² – 2x

Đáp án cần chọn là: C

Bài 14: Chọn câu đúng.

A. (x – 1)(x² + x + 1) = x³ – 1            

B. (x – 1)(x + 1) = 1 – x²

C. (x + 1)(x – 1) = x² + 1                   

D. (x² + x + 1)(x – 1) = 1 – x²

Lời giải

Ta có

+) (x – 1)(x + 1) = x.x + x – x – 1 = x² – 1 nên phương án B sai, C sai

+) (x – 1)(x² + x + 1)

= x.x² + x.x + x.1 – x² – x – 1

= x³ + x² + x – x² – x – 1 = x³ – 1 nên phương án D sai, A đúng

Đáp án cần chọn là: A

Bài 15: Chọn câu đúng.

A. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 17x – 1

B. (2x – 1)(3x² -7x + 5) = 6x³ – 4x² + 4x – 5

C. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 10x – 5

D. (2x – 1)(3x² -7x + 5) = 6x³ – 17x² + 17x – 5

Lời giải

Ta có (2x – 1)(3x² -7x + 5) = 2x.3x² + 2x.(-7x) + 2x.5 – 3x² – (-7x) – 1.5

                                      = 6x³ – 14x² + 10x – 3x² + 7x – 5

                                      = 6x³ – 17x² + 17x – 5

Đáp án cần chọn là: D

Bài 16: Cho 4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14). Kết quả x bằng:

A. 8            

B. -8           

C. 6            

D. -6

Lời giải

Ta có

4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14)

⇔ 72 – 20x – 36x + 84 = 30x – 240 – 6x – 84

⇔ -56x + 156 = 24x – 324

⇔ 24x + 56x = 156 +324

⇔ 80x = 480

⇔ x = 6

Vậy x = 6

Đáp án cần chọn là: C

Bài 17: Cho 2x(3x – 1) – 3x(2x – 3) = 11. Kết quả x bằng:

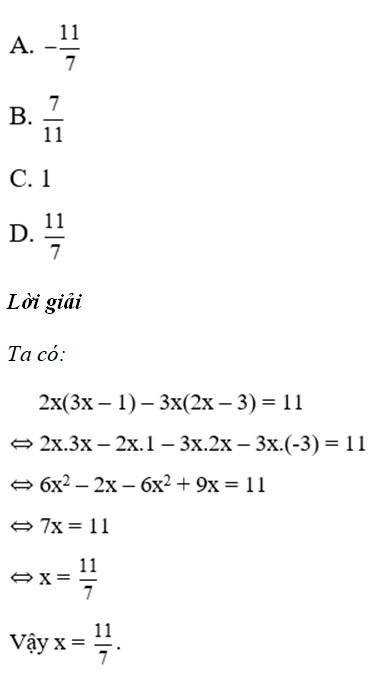
Đáp án cần chọn là: D

Bài 18: Cho biểu thức P = 2x(x² – 4) + x²(x² – 9). Hãy chọn câu đúng:

A. Giá trị của biểu thức P tại x = 0 là 1

B. Giá trị của biểu thức P tại x = 2 là -20

C. Giá trị của biểu thức P tại x = -2 là 30

D. Giá trị của biểu thức P tại x = -9 là 0

Lời giải

Thay x = 0 vào P ta được

P = 2.0(0² – 4) + 0²(0² – 9) = 0 nên A sai.

Thay x = -2 vào P ta được

P = 2.(-2).((-2)² – 4) + (-2)².((-2)² – 9) = -20 nên C sai.

Thay x = -9 vào P ta được

P = 2.(-9).((-9)² – 4) + (-9)².((-9)² – 9) = 4446 nên D sai.

Thay x = 2 vào P ta được

P = 2.2.(2² – 4) + 2²(2² – 9) = 4.0 + 4.(-5) = -20 nên B đúng

Đáp án cần chọn là: B

Bài 19: Cho biểu thức M = x²(3x – 2) + x(-3x² + 1). Hãy chọn câu đúng

A. Giá trị của biểu thức M tại x = 0 là 1

B. Giá trị của biểu thức M tại x = 1 là 1

C. Giá trị của biểu thức M tại x = -2 là -6

D. Giá trị của biểu thức M tại x = 3 là -15

Lời giải

Ta có M = x²(3x – 2) + x(-3x² + 1) = x².3x + x².(-2) + x.(-3x²) + x.1

                                                    = 3x³ – 2x² – 3x³ + x = -2x² + x

Thay x = 0 vào M = -2x² + x ta được

M = -2.0² + 0 = 0 nên A sai.

Thay x = 1 vào M = -2x² + x ta được

M = -2.1² + 1 = -1 nên B sai

Thay x = -2 vào M = -2x² + x ta được

M = -2.(-2)² + (-2) = -10 nên C sai.

Thay x = 3 vào M = -2x² + x ta được

M = -2.3² + 3 = -15 nên D đúng

Đáp án cần chọn là: D

Bài 20: Cho biểu thức A = x(x + 1) + (1 – x)(1 + x) – x. Khẳng định nào sau đây là đúng.

A. A = 2 – x

B. A < 1     

C. A > 0     

D. A > 2

Lời giải

Ta có A = x(x + 1) + (1 – x)(1 + x) – x = x² + x + 1 + x – x – x² – x = 1

Suy ra A = 1 > 0

Đáp án cần chọn là: C

Bài 21: Cho bểu thức B = (2x – 3)(x +7) – 2x(x + 5) – x. Khẳng định nào sau đây là đúng.

A. B = 21 – x

B. B < -1    

C. B > 0     

D. 10 < B < 20

Lời giải

Ta có B = (2x – 3)(x +7) – 2x(x + 5) – x

          = 2x.x + 2x.7 – 3.x – 3.7 – 2x.x – 2x.5 – x

          = 2x² + 14x – 2x – 21 – 2x² – 10x – x

          = (2x² – 2x²) + (14x – 3x – 10x – x) – 21 = -21

Đáp án cần chọn là: B

Bài 22: Cho biểu thức C = x(y + z) – y(z + x) – z(x – y). Chọn khẳng định đúng.

A. Biểu thức C không phụ thuộc vào x; y; z

B. Biểu thức C phụ thuộc vào cả x; y; z

C. Biểu thức C chỉ phụ thuộc vào y

D. Biểu thức C chỉ phụ thuộc vào z

Lời giải

Ta có C = x(y + z) – y(z + x) – z(x – y)

= xy + xz – yz – xy – zx + xy

= (xy – xy) + (zy – zy) + (xz – zx) = 0

Nên C không phụ thuộc vào x; y; z

Đáp án cần chọn là: A

Bài 23: Cho biểu thức D = x(x – y) + y(x + y) – (x + y)(x – y) – 2y². Chọn khẳng định đúng.

A. Biểu thức D có giá trị là một số dương

B. Biểu thức D có giá trị là một số âm

C. Biểu thức D có giá trị phụ thuộc vào y, x

D. Biểu thức D có giá trị là 0

Lời giải

Ta có

D = x(x – y) + y(x + y) – (x + y)(x – y) – 2y²

= x² – xy + xy + y² – (x² – xy + xy – y²) – 2y²

= x² + y² – (x² – y²) – 2y²

= x² + y² – x² + y² – 2y²

= (x² – x²) + (y² + y² – 2y²)

= 0

Nên D = 0

Đáp án cần chọn là: D

Bài 24: Biểu thức D = x(x^2n-1 + y) – y(x + y^2n-1) + y²ⁿ – x²ⁿ + 5, D có giá trị là:

A. 2y²ⁿ        

B. -5           

C. x²ⁿ          

D. 5

Lời giải

Ta có

D = x(x^2n-1 + y) – y(x + y^2n-1) + y²ⁿ – x²ⁿ + 5

= x.x^2n-1 + x.y – y.x – y.y^2n-1 + y²ⁿ – x²ⁿ + 5

= x²ⁿ + xy – xy – y²ⁿ + y²ⁿ – x²ⁿ + 5

= (x²ⁿ – x²ⁿ) + (xy – xy) + (y²ⁿ – y²ⁿ) + 5

= 0 + 0 + 0 + 5 = 5

Đáp án cần chọn là: D

Bài 25: Rút gọn biểu thức N = 2xⁿ(3xⁿ⁺² – 1) – 3xⁿ⁺²(2xⁿ – 1) ta được

A. N = 2xⁿ + 3xⁿ⁺²                   

B. N = -2xⁿ – 3xⁿ⁺²

C. N = -2xⁿ + 3xⁿ⁺²                  

D. N = -2xⁿ + xⁿ⁺²

Lời giải

Ta có N = 2xⁿ(3xⁿ⁺² – 1) – 3xⁿ⁺²(2xⁿ – 1)

N = 2xⁿ(3xⁿ⁺² – 1) – 3xⁿ⁺²(2xⁿ – 1)

= 2xⁿ.3xⁿ⁺² – 2xⁿ.1 – 3xⁿ⁺².2xⁿ – 3xⁿ⁺².(-1)

= 6xⁿ⁺ⁿ⁺² – 2xⁿ – 6.xⁿ⁺²⁺ⁿ + 3xⁿ⁺²

= 6x²ⁿ⁺² – 6x²ⁿ⁺² – 2xⁿ + 3xⁿ⁺²

= – 2xⁿ + 3xⁿ⁺²

Vậy N = – 2xⁿ + 3xⁿ⁺²

Đáp án cần chọn là: C

Bài 26: Cho hai số tự nhiên n và m. Biết rằng n chia 5 dư 1, m chia 5 dư 4. Hãy chọn câu đúng:

A. m.n chia 5 dư 1                   

B. m – n chia hết cho 5

C. m + n chia hết cho 5            

D. m.n chia 5 dư 3

Lời giải

Ta có n chia 5 dư 1 nên n = 5p + 1 (0 < p < n; p ∈ N); m chia 5 dư 4 nên 

m = 5q + 4 (0 < q < m ; q ∈ N)

Khi đó m.n = (5p + 1)(5q + 4) = 25pq + 20p + 5q + 4 = 5(5pq + 4p + q) + 4 

Mà 5(5pq + 4p + q) ⋮ nên m.n chia 5 dư 4 , phương án A sai, D sai.

Ta có m – n = 5q + 4 − (5p + 1) = 5q − 5p + 3

Mà 5p ⋮ 5; 5q ⋮ 5 nên m − n chia 5 dư 3 , phương án B sai.

Ta có m + n = 5q + 4 + 5p + 1 = 5q + 5p + 5 = 5(q + p + 1) ⋮ 5 nên C đúng.

Đáp án cần chọn là: C

Bài 27: Cho hai a, b là những số nguyên và (2a + b) ⋮ 13; (5a – 4b) ⋮ 13. Hãy chọn câu đúng:

A. a – 6b chia hết cho 13         

B. a – 6b chia cho 13 dư 6

C. a – 6b chia cho 13 dư 1        

D. a – 6b chia cho 13 dư 3

Lời giải

Ta có (2a + b) ⋮ 13; (5a – 4b) ⋮ 13, suy ra 2(2a + b) ⋮ 13

Từ đó ta có (5a – 4b) - 2(2a + b) ⋮ 13 hay a – 6b ⋮ 13

Đáp án cần chọn là: A

Bài 28: Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao 2 đơn vị. Biểu thức tính diện tích hình thang là

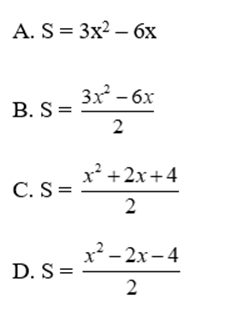
Lời giải

Gọi x (x > 2) là độ dài đáy nhỏ của hình thang

Theo giả thiết ta có độ dài đáy lớn là 2x, chiều cao của hình thang là x – 2

Diện tích hình thang là

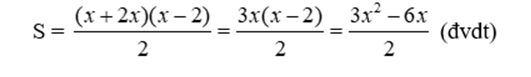
Đáp án cần chọn là: B

Bài 29: Cho hình chữ nhật có chiều dài lớn hơn chiều rộng là 5 đơn vị. Biểu thức tính diện tích hình chữ nhật là:

A. S = x² + 5x

B. S =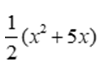 

C. S = 2x + 5

D. S = x² – 5x

Lời giải

Gọi x ( x > 0) là chiều rộng của hình chữ nhật

Theo giả thiết ta có chiều dài hình chữ nhật là x + 5

Diện tích hình chữ nhật là S = x(x + 5) = x² + 5x (đvdt)

Đáp án cần chọn là: A

Bài 30: Giá trị của biểu thức M = x(x³ + x² – 3x – 2)- (x² – 2)(x² + x – 1) là

A. 2            

B. 1            

C. – 1         

D. – 2

Lời giải

Ta có

M = x(x³ + x² – 3x – 2)- (x² – 2)(x² + x – 1)

= x.x³ + x.x² – 3x.x – 2.x – (x².x² + x².x – x² – 2x² – 2x + 2)

= x⁴ + x³ – 3x² – 2x – (x⁴ + x³ – 3x² – 2x + 2)

= x⁴ + x³ – 3x² – 2x – x⁴ – x³ + 3x² + 2x – 2

= - 2

Vậy M = -2

Đáp án cần chọn là: D

Bài 31: Giá trị của biểu thức P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x là

A. P = -8    

B. P = 8      

C. P = 2      

D. P = -2

Lời giải

Ta có

P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x

= 3x.2x + 3x.3 – 1.2x – 1.3 – (x.6x – x – 5.6x – 5.(-1)) – 38x

= 6x² + 9x – 2x – 3 – 6x² + x + 30x – 5 – 38x

= (6x² – 6x²) + (9x – 2x + x + 30x – 38x) – 3 – 5

= -8

Vậy P = -8

Đáp án cần chọn là: A

Bài 32: Cho A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11); B = x(2x + 1) – x²(x + 2) + x³ – x + 3. Chọn khẳng định đúng

A. A = B    

B. A = 25B 

C. A = 25B + 1

D. A = B/2 

Lời giải

A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)

= 3x.2x + 3x.3 + 7.2x + 7.3 – (3x.2x + 3x.11 – 5.2x – 5.11)

= 6x² + 9x + 14x + 21 – (6x² + 33x – 10x – 55)

= 6x² + 23x + 21 – 6x² – 33x + 10x + 55 = 76

B = x(2x + 1) – x²(x + 2) + x³ – x + 3

= x.2x + x – (x².x + 2x²) + x³ – x + 3

= 2x² + x – x³ – 2x² + x³ – x + 3 = 3

Từ đó ta có A = 76; B = 3 mà 76 = 25.3 + 1 nên A = 25B + 1

Đáp án cần chọn là: C

Bài 33: Cho M = -3(x – 4)(x – 2) + x(3x – 18) – 25; N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1). Chọn khẳng định đúng.

A. M – N = 30

B. M – N = -30

C. M – N = 20

D. M – N = -68

Lời giải

M = -3(x – 4)(x – 2) + x(3x – 18) – 25

= -3(x² – 2x – 4x + 8) + x.3x + x.(-18) – 25

= -3x² + 6x + 12x – 24 + 3x² – 18x – 25

= (-3x² + 3x²) + (6x + 12x – 18x) – 24 – 25

= -49

N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1)

= x.x + x.7 – 3.x – 3.7 – (2x.x + 2x.2 – x – 1.2) + x.x + x.(-1)

= x ² + 7x – 3x – 21 – 2x² – 4x + x + 2 + x² – x

= (x² – 2x² + x²) + (7x – 3x – 4x + x – x) – 21 + 2

= -19

Vậy M = -49; N = -19 ⇒ M – N = -30

Đáp án cần chọn là: B

Bài 34: Gọi x là giá trị thỏa mãn 5(3x + 5) – 4(2x – 3) = 5x + 3(2x – 12) + 1. Khi đó

A. x > 18    

B. x < 17    

C. 17 < x < 19

D. 18 < x < 20

Lời giải

Ta có

5(3x + 5) − 4(2x − 3) = 5x + 3(2x − 12) + 1

⇔ 15x + 25 − 8x + 12 = 5x + 6x – 36 + 1

⇔ 7x + 37 = 11x − 35

⇔ 4x = 72

⇔ x = 18

Vậy x = 18. 

Suy ra 17 < x < 19 nên chọn C.

Đáp án cần chọn là: C

Bài 35: Gọi x là giá trị thỏa mãn (3x – 4)(x – 2) = 3x(x – 9) – 3. Khi đó

A. x < 0      

B. x < -1     

C. x > 2      

D. x > 0

Lời giải

Ta có (3x – 4)(x – 2) = 3x(x – 9) – 3

⇔ 3x.x+ 3x.(-2) – 4.x – 4.(-2) = 3x.x + 3x.(-9) – 3

⇔ 3x² – 6x -4x + 8 = 3x² – 27x – 3

⇔ 17x = -11 ⇔ x =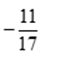 

Vậy x =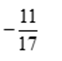 

Đáp án cần chọn là: A