Toptailieu.vn xin giới thiệu 35 câu trắc nghiệm Những hằng đẳng thức đáng nhớ (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 8 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

35 câu trắc nghiệm Những hằng đẳng thức đáng nhớ (có đáp án) chọn lọc

Bài 1: Chọn câu đúng.

A. (A + B)² = A² + 2AB + B²   

B. (A + B)² = A² + AB + B²

C. (A + B)² = A² + B²              

D. (A + B)² = A² – 2AB + B²

Lời giải

Ta có (A + B)² = A² + 2AB + B²

Đáp án cần chọn là: A

Bài 2: Chọn câu đúng.

A. (A – B)(A + B) = A² + 2AB + B²

B. (A + B)(A – B) = A² – B²

C. (A + B)(A – B) = A² – 2AB + B²

D. (A + B)(A – B) = A² + B²

Lời giải

Ta có A² – B² = (A – B)(A + B)

Đáp án cần chọn là: B

Bài 3: Chọn câu sai.

A. (x + y)² = (x + y)(x + y)       

B. x² – y² = (x + y)(x – y)

C. (-x – y)² = (-x)² – 2(-x)y + y²

D. (x + y)(x + y) = y² – x²

Lời giải

Ta có (x + y)(x + y) = (x + y)² = x² + 2xy + y² ≠ y² – x² nên câu D sai.

Đáp án cần chọn là: D

Bài 4: Chọn câu sai.

A. (x + 2y)² = x² + 4xy + 4y²    

B. (x – 2y)² = x² – 4xy + 4y²

C. (x – 2y)² = x² – 4y²                       

^D. (x – 2y)(x + 2y) = x² – 4y²

Lời giải

Ta có (x + 2y)² = x² + 2x.2y + (2y)² = x² + 4xy + 4y² nên A đúng

(x – 2y)² = x² – 2x.2y + (2y)² = x² – 4xy + 4y² nên B đúng, C sai.

(x – 2y)(x + 2y) = x² – (2y)² = x² – 4y² nên D đúng

Đáp án cần chọn là: C

Bài 5: Khai triển 4x² – 25y² theo hằng đẳng thức ta được

A. (4x – 5y)(4x + 5y)               

B. (4x – 25y)(4x + 25y) 

C. (2x – 5y)(2x + 5y)               

D. (2x – 5y)²

Lời giải

Ta có 4x² – 25y² = (2x)² – (5y)² = (2x – 5y)(2x + 5y)

Đáp án cần chọn là: C

Bài 6: Khai triển 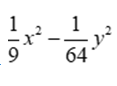 theo hằng đẳng thức ta được

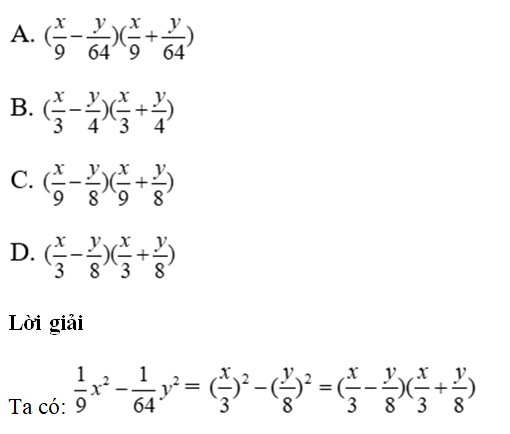
Đáp án cần chọn là: D

Bài 7: Khai triển (3x – 4y)² ta được

A. 9x² – 24xy + 16y²               

B. 9x² – 12xy + 16y²

C. 9x² – 24xy + 4y²                  

D. 9x² – 6xy + 16y²

Lời giải

Ta có (3x – 4y)² = (3x)² – 2.3x.4y + (4y)² = 9x² – 24xy + 16y²

Đáp án cần chọn là: A

Bài 8: Khai triển 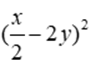  ta được

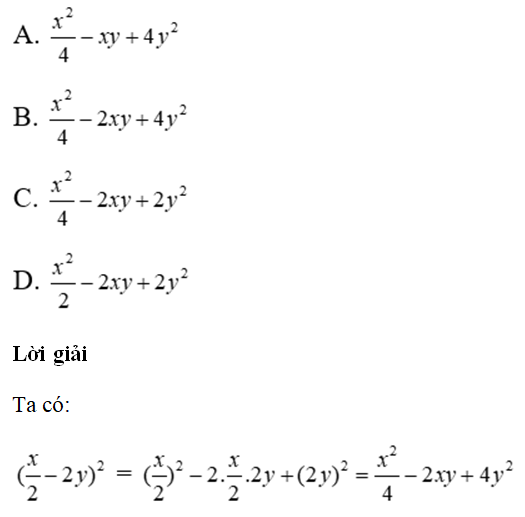
Đáp án cần chọn là: B

Bài 9: Biểu thức 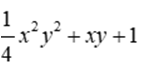 bằng

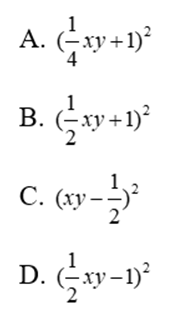
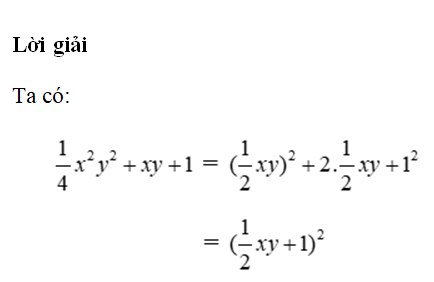
Đáp án cần chọn là: B

Bài 10: Viết biểu thức 25x² – 20xy + 4y² dưới dạng bình phương của một hiệu

A. (5x – 2y)²

B. (2x – 5y)²

C. (25x – 4y)²

D. (5x + 2y)²

Lời giải

Ta có 25x² – 20xy + 4y² = (5x)² – 2.5x.2y + (2y)² = (5x – 2y)²

Đáp án cần chọn là: A

Bài 11: Chọn câu đúng

A. (c + d)² – (a + b)² = (c + d + a + b)(c + d – a + b)

B. (c – d)² – (a + b)² = (c – d + a + b)(c – d – a + b)

C. (a + b + c – d)(a + b – c + d) = (a + b)² – (c – d)²

D. (c – d)² – (a – b)² = (c – d + a – b)(c – d – a – b)

Lời giải

Ta có

(c + d)² – (a + b)² = (c + d + a + b)(c + d – (a + b)) = (c + d + a + b)(c + d – a – b) nên A sai

(c – d)² – (a + b)² = (c – d + a + b)[c – d – (a + b)] = (c – d + a + b)(c – d – a – b) nên B sai

(c – d)² – (a – b)² = (c – d + a – b)(c – d – (a – b)) = (c – d + a – b)(c – d – a + b) nên D sai

(a + b + c – d)(a + b – c + d) = [(a + b) + (c – d)][(a + b) – (c – d)] = (a + b)² – (c – d)² nên C đúng

Đáp án cần chọn là: C

Bài 12: Chọn câu đúng

A. 4 – (a + b)² = (2 + a + b)(2 – a + b)

B. 4 – (a + b)² = (4 + a + b)(4 – a – b)

C. 4 – (a + b)² = (2 + a – b)(2 – a + b)

D. 4 – (a + b)² = (2 + a + b)(2 – a – b)

Lời giải

Ta có 4 – (a + b)² = 2² – (a + b)² = (2 + a + b)[2 – (a + b)]

                                                = (2 + a + b)(2 – a – b)

Đáp án cần chọn là: D

Bài 13: Rút gọn biểu thức A = (3x – 1)² – 9x(x + 1) ta được

A. -15x + 1 

B. 1            

C. 15x + 1            

D. – 1

Lời giải

Ta có A = (3x – 1)² – 9x(x + 1)

          = (3x)² – 2.3x.1 + 1 – (9x.x + 9x)

          = 9x² – 6x + 1 – 9x² – 9x

          = -15x + 1

Đáp án cần chọn là: A

Bài 14: Rút gọn biểu thức A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4), ta được2 ^{+ 4(x – 5)}2 ^{– 9(}

A. 342        

B. 243        

C. 324        

D. -324

Lời giải

Ta có A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4)

          = 5(x² + 2.x.4 + 16) + 4(x² – 2.x.5 + 5²) – 9(x² – 4²)

          = 5(x² + 8x + 16) + 4(x² – 10x + 25) – 9(x² – 4²)

          = 5x² + 40x + 80 + 4x² – 40x + 100 – 9x² + 144

=

(5x² + 4x² – 9x²) + (40x – 40x) + (80 +100 + 144)

          = 324

Đáp án cần chọn là: C

Bài 15: Rút gọn biểu thức B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7) ta được

A. 0            

B. 1            

C. 19          

D. – 19

Lời giải

Ta có B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7)

          = 2a² + 2a – 3a – 3 – (a² – 8a + 16) – (a² + 7a)

          = 2a² + 2a – 3a – 3 – a² + 8a – 16 – a² – 7a

          = - 19

Đáp án cần chọn là: D

Bài 16: Cho B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1). Chọn câu đúng.

A. B < 12   

B. B > 13   

C. 12 < B< 14

D. 11 < B < 13

Lời giải

Ta có B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1).

          = (x²)² +2.x².4 + 3² – (x².x² + x².3) – 3(x² – 1)       

          = x⁴ + 6x² + 9 – x⁴ – 3x² – 3x² + 3 = 12

Đáp án cần chọn là: D

Bài 17: Cho 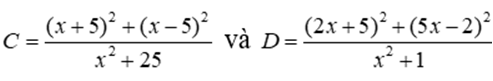 . Tìm mối quan hệ giữa C và D.

A. D = 14C + 1

B. D = 14C 

C. D = 14C – 1

D. D = 14C – 2

Lời giải

Ta có:

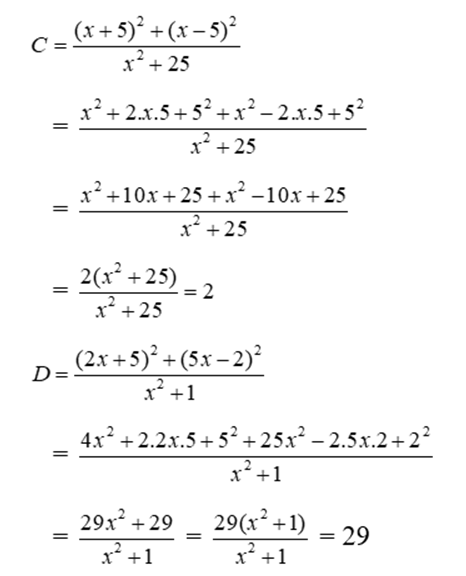
Vậy D = 29; C = 2 suy ra D = 14C + 1 (do 29 = 14.2 + 1)

Đáp án cần chọn là: A

Bài 18: Cho M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14).

Tìm mối quan hệ giữa M và N

A. 2N – M = 60

B. 2M – N = 60

C. M> 0, N < 0

D. M > 0, N > 0

Lời giải

Ta có

M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12

= 4(x² + 2x + 1) + (4x² + 4x + 1) – 8(x² – 1) – 12x

= 4x² + 8x + 4 + 4x² + 4x + 1 – 8x² +8 – 12x

= (4x² + 4x² – 8x²) + (8x + 4x – 12x) + 4 + 1 +8

= 13

N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14)

= 2(x² – 2x + 1) – 4(9 + 6x + x²) + 2x² + 28x

= 2x² – 4x + 2 – 36 – 24x – 4x² + 2x² + 28x

= (2x² +2x² – 4x²) + (-4x – 24x + 28x) + 2 – 36

= -34

Suy ra M = 13, N = -34 ⇔ 2M – N = 60

Đáp án cần chọn là: B

Bài 19: Có bao nhiêu giá trị x thỏa mãn (2x – 1)² – (5x – 5)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

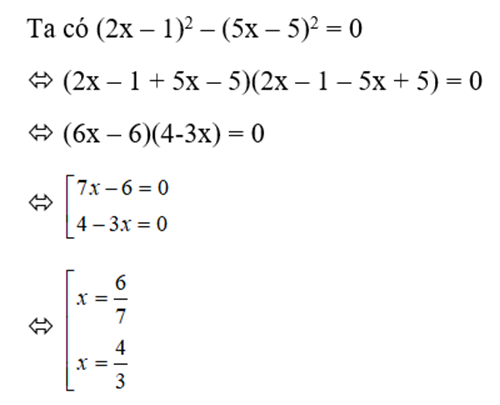
Vậy có hai giá trị của x thỏa mãn yêu cầu

Đáp án cần chọn là: C

Bài 20: Có bao nhiêu giá trị x thỏa mãn (2x + 1)² – 4(x + 3)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

Ta có:

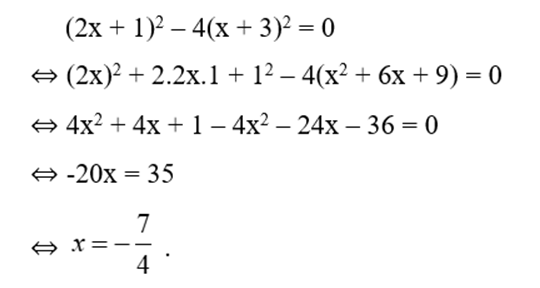
Vậy có một giá trị của x thỏa mãn yêu cầu.

Đáp án cần chọn là: B

Bài 21: Tìm x biết (x – 6)(x + 6) – (x + 3)² = 9

A. x = -9     

B. x = 9      

C. x = 1      

D. x = -6

Lời giải

Ta có (x – 6)(x + 6) – (x + 3)² = 9

⇔ x² – 36 – (x² + 6x + 9) = 9

⇔ x² – 36 – x² – 6x – 9 – 9 = 0

⇔ - 6x – 54 = 0

⇔ 6x = -54

⇔ x = -9

Vậy x = -9

Đáp án cần chọn là: A

Bài 22: Tìm x biết (3x – 1)² + 2(x + 3)² + 11(1 + x)(1 – x) = 6

A. x = -4     

B. x = 4      

C. x = -1     

D. x = -2

Lời giải

Ta có (3x – 1)² + 2(x + 3)² + 11(1 + x)(1 – x) = 6

⇔ (3x)² – 2.3x.1 + 1² + 2(x² + 6x + 9) + 11(1 – x²) = 6

⇔ 9x² – 6x + 1 + 2x² + 12x + 18 + 11 – 11x² = 6

⇔ (9x² + 2x² – 11x²) + (-6x + 12x) = 6 – 1 – 11 – 18

⇔ 6x = -24 ⇔ x = -4

Vậy x = -4

Đáp án cần chọn là: x = -4

Bài 23: So sánh A = 2016.2018.a và B = 2017.a (với a > 0)

A. A = B    

B. A < B     

C. A > B     

D. A ≥ B

Lời giải

Ta có A = 2016.2018.a = (2017 – 1)(2017 + 1)a = (2017² – 1)a

Vì 2017² – 1 < 2017² và a > 0 nên (2017² – 1)a < 2017²a hay A < B

Đáp án cần chọn la: B

Bài 24: So sánh A = 2019.2021.a và B = (2019² + 2.2019 + 1)a (với a > 0)

A. A= B     

B. A ≥ B     

C. A > B     

D.A < B

Lời giải

Ta có A = 2019.2021.a = (2020 – 1)(2020 + 1)a = (2020² – 1)a

Và B = (2019² + 2.2019 + 1)a = (2019 + 1)²a = 2020²a

Vì 2020² – 1 < 2020² và a > 0 nên (2020² – 1)a < 2020²a hay A < B

Đáp án cần chọn là: D

Bài 25: So sánh M = 2³² và N = (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

A. M > N    

B. M < N    

C. M = N    

D. M = N – 1

Lời giải

Ta có N = (2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

(2¹⁶ + 1) = 3(2² + 1)(2⁴ + 1)(2⁸ + 1)

(2¹⁶ + 1) = [(2² – 1)(2² + 1)](2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

          = (2⁴ – 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

          = (2⁸ – 1)(2⁸ + 1)(2¹⁶ + 1)

          = (2¹⁶ - 1)(2¹⁶ + 1) = (2¹⁶)² – 1 = 2³² – 1

Mà 2³² – 1 < 2³² ⇒ N < M

Đáp án cần chọn là: A

Bài 26: Chọn câu đúng về giá trị các biểu thức sau mà không tính cụ thể

A = 1 + 15(4² + 1)(4⁴ + 1)(4⁸ + 1) và B = (4³)⁵ + (4⁵)³

A. A = B + 2

B. B = 2A   

C. A = 2B   

D. A = B

Lời giải

Ta có A = 1 + 15(4² + 1)(4⁴ + 1)(4⁸ + 1)

          = 1 + (4² – 1)(4² + 1)(4⁴ + 1)(4⁸ + 1)

          = 1 + [(4²)² – 1](4⁴ + 1)(4⁸ + 1)

          = 1 + (4⁴ – 1)(4⁴ + 1)(4⁸ + 1) = 1 + [(4⁴)² – 1](4⁸ + 1)

          = 1 + (4⁸ – 1)(4⁸ + 1) = 1 + (4⁸)² – 1 = 1 + 4¹⁶ – 1 = 4¹⁶

          = 4.4¹⁵

Và B = (4³)⁵ + (4⁵)³ = 4^3.5 + 4^5.3 = 4¹⁵ + 4¹⁵ = 2.4¹⁵

Vì A = 4.4¹⁵; B = 2.4¹⁵ ⇒ A = 2B

Đáp án cần chọn là: C

Bài 27: Cho P = -4x² + 4x – 2. Chọn khẳng định đúng.

A. P ≤ -1    

B. P > -1     

C. P > 0      

D. P ≤ - 2

Lời giải

Ta có P = -4x² + 4x – 2

          = -4x² + 4x – 1 – 1 = -(4x² – 4x + 1) – 1

          = - 1 – (2x – 1)²

Nhận thấy –(2x – 1)² ≤ 0

⇒ -1 – (2x – 1)² ≤ -1, Ɐx hay P ≤ -1.

Đáp án cần chọn là: A

Bài 28: Cho T = -9x² + 6x – 5. Chọn khẳng định đúng

A. T < -4    

B. T ≥ -4    

C. T > -4    

D.T ≤ -4

Lời giải

Ta có T = -9x² + 6x – 5 = -9x² + 6x – 1 – 4

          = -4 – (9x² – 6x + 1) = -4 – (3x – 1)²

Nhận thấy –(3x – 1)² ≤ 0 ⇒ -4 – (3x – 1)² ≤ -4, Ɐx hay T ≤ -4

Đáp án cần chọn là: D

Bài 29: Tìm giá trị lớn nhất của biểu thức Q = 8 – 8x – x²

A. 8            

B. 11          

C. -4           

D. 24

Lời giải

Ta có Q = 8 – 8x – x²

= -x² – 8x – 16 + 16 + 8 = -(x + 4)² + 24

= 24 – (x + 4)²

Nhận thấy (x + 4)² ≥ 0; Ɐx

⇒ 24 – (x + 4)² ≤ 24

Dấu “=” xẩy ra khi (x + 4)² = 0 ⇔ x = -4

Giá trị lớn nhất của Q là 24 khi x = -4

Đáp án cần chọn là: D

Bài 30: Tìm giá trị lớn nhất của biểu thức B = 4 – 16x² – 8x

A. 5            

B. -5           

C. 8            

D.  

Lời giải

Ta có B = 4 – 16x² – 8x

          = 5 – (16x² + 8x + 1) = 5 – [(4x)² + 2.4x.1 + 1²]

          = 5 – (4x + 1)²

Nhận thấy (4x + 1)² ≥ 0; Ɐx

⇒ 5 – (4x + 1)² ≤ 5

Dấu “=” xảy ra khi (4x + 1)² = 0 ⇔ x = 

Đáp án cần chọn là: A

Bài 31: Biểu thức E = x² – 20x +101 đạt giá trị nhỏ nhất khi

A. x = 9      

B. x = 10    

C. x = 11    

D.x = 12

Lời giải

Ta có E = x² – 20x +101 = x² – 2.x.10 + 100 + 1 = (x – 10)² + 1

Vì (x – 10)² ≥ 0; Ɐx ⇒ (x – 10)² + 1 ≥ 1

Dấu “=” xảy ra khi (x – 10)² = 0 ⇔ x – 10 = 0 ⇔ x = 10

Vậy giá trị nhỏ nhất của E là 1 khi x = 10

Đáp án cần chọn là: B

Bài 32: Biểu thức F = x² – 12x +34 đạt giá trị nhỏ nhất khi

A. x = 6      

B. x = -6     

C. x = 8      

D. x = 2

Lời giải

Ta có

F = x² – 12x +34 = x² – 2.x.6 + 6² – 2 = (x – 6)² – 2

Vì (x – 6)² ≥ 0; Ɐx ⇒ (x – 6)² – 2 ≥ - 2

Dấu “=” xảy ra khi (x – 6)² = 0 ⇔ x – 6 = 0 ⇔ x = 6

Vậy giá trị nhỏ nhất của E là -2 khi x = 6

Đáp án cần chọn là: A

Bài 33: Biểu thức K = x² – 6x + y² – 4y + 6 có giá trị nhỏ nhất là

A. 6            

B. 1            

C. -7           

D. 7

Lời giải

Ta có K = x² – 6x + y² – 4y + 6

          = x² – 2x.3 + 9 + y² – 2.y.2 + 4 – 7

          = (x – 3)² + (y – 2)² – 7

Vì (x – 3)² ≥ 0; (y – 2)² ≥ 0; Ɐx; y nên (x – 3)² + (y – 2)² – 7 ≥ -7

Dấu “=” xảy ra khi  ⇔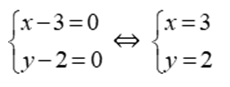  

Vậy giá trị nhỏ nhất của K là -7 khi x = 3; y = 2

Đáp án cần chọn là: C

Bài 34: Biểu thức J = x² – 8x + y² + 2y+ 5 có giá trị nhỏ nhất là

A. -12         

B. 5            

C. 12          

D. -5

Lời giải

Ta có J = x² – 8x + y² + 2y + 5

          = x² – 2.x.4 + 16 + y² + 2.y.1 + 1 – 12

          = (x – 2)² + (y + 1)² – 12

Vì (x – 2)² ≥ 0; (y + 1)² ≥ 0; Ɐx; y nên (x – 2)² + (y + 1)² – 12 ≥ -12

Dấu “=” xảy ra khi  ⇔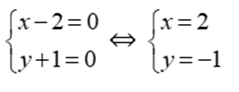   

Vậy giá trị nhỏ nhất của J là -12 khi x = 2; y = -1

Đáp án cần chọn là: A

Bài 35: Giá trị nhỏ nhất của biểu thức I = (x² + 4x + 5)(x² + 4x + 6) + 3 là

A. 4            

B. 5            

C. 3            

D. 2

Lời giải

Ta có I = (x² + 4x + 5)(x² + 4x + 6) + 3

          = (x² + 4x + 5)(x² + 4x + 5 + 1) + 3

          = (x² + 4x + 5)² + (x² + 4x + 5) + 3

          = (x² + 4x + 5)² + (x² + 4x + 4) + 4

          = (x² + 4x + 5)² + (x + 2)² + 4

Ta có x² + 4x + 5 = x² + 4x + 4 + 1

= (x + 2)² + 1 ≥ 1; Ɐx nên (x² + 4x + 5)² ≥ 1; Ɐx

Và (x + 2)² ≥ 0; Ɐx (x² + 4x + 5)² + (x + 2)² + 4 ≥ 1 + 4

⇔ (x² + 4x + 5)² + (x + 2)² + 4 ≥ 5

Dấu “=” xảy ra khi 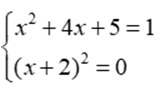  ⇒ x = -2

Vậy giá trị nhỏ nhất của I là 5 khi x = -2

Đáp án cần chọn là: B