Toptailieu.vn xin giới thiệu 30 bài tập trắc nghiệm Cung chứa góc (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Cung chứa góc

Câu 1: Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là:

A. Đường tròn đường kính AB          

B. Nửa đường tròn đường kính AB

C. Đường tròn đường kính  

D. Đường tròn bán kính AB

Lời giải:

Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB

Đáp án cần chọn là: A

Câu 2: Đường tròn đường kính CD là quỹ tích của điểm nào dưới đây?

A. Quỹ tích các điểm P nhìn đoạn thẳng CD cho trước dưới một góc 60^o.

B. Quỹ tích các điểm N nhìn đoạn thẳng CD cho trước dưới một góc 45^o.

C. Quỹ tích các điểm M nhìn đoạn thẳng CD cho trước dưới một góc vuông.

D. Quỹ tích các điểm Q thuộc đường trung trực của CD

Lời giải:

Quỹ tích các điểm M nhìn đoạn thẳng CD cho trước dưới một góc vuông là đường tròn đường kính CD

Đáp án cần chọn là: C

Câu 3: Với đoạn thẳng AB và góc  (O^o < α < 180^o) cho trước thì quỹ tích các điểm M thỏa mãn 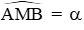 là:

A. Hai cung chứa góc α dựng trên đoạn AB. Hai cung này không đối xứng nhau qua AB

B. Hai cung chứa góc α dựng trên đoạn AB và không lấy đoạn AB

C. Hai cung chứa góc α dựng trên đoạn AB. Hai cung này đối xứng nhau qua AB

D. Một cung chứa góc α dựng trên đoạn AB

Lời giải:

Với đoạn thẳng AB và góc  (0^o < α < 180^o) cho trước thì quỹ tích các điểm M thỏa mãn 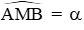 là hai cung chứa góc  dựng trên đoạn AB

Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB. Hai điểm A, B được coi là thuộc quỹ tích

Đáp án cần chọn là: C

Câu 4: Cho hình vẽ sau, chọn kết luận đúng:

A. Điểm E thuộc cung chứa góc 80^o dựng trên đoạn AC

B. Điểm B, D thuộc cung chứa góc 80^o dựng trên đoạn AC

C. Ba điểm B, E, D cùng thuộc cung chứa góc 80^o dựng trên đoạn AC

D. Năm điểm A, B, C, D, E cùng thuộc một đường tròn

Lời giải:

Quan sát hình vẽ ta thấy các điểm B, D thuộc cung chứa góc 80^o dựng trên đoạn AC, còn điểm E thuộc cung chứa góc 75^o dựng trên đoạn AC

Do đó chỉ có đáp án 2 điểm B, D thuộc cung chứa góc 80^o dựng trên đoạn AC là đúng

Đáp án cần chọn là: B

Câu 5: Cho tam giác ABC có BC cố định và góc A bằng 50^o. Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D

A. Một cung chứa góc 115^o dựng trên đoạn BC

B. Một cung chứa góc 115^o dựng trên đoạn AC

C. Hai cung chứa góc 115^o dựng trên đoạn AB

D. Hai cung chứa góc 115^o dựng trên đoạn BC

Lời giải:

Quỹ tích của điểm D là hai cung chứa góc 115^o dựng trên đoạn BC

Đáp án cần chọn là: D

Câu 6: Cho tam giác ABC có BC cố định và góc A bằng 60^o. Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D

A. Hai cung chứa góc 120^o dựng trên đoạn BC

B. Một cung chứa góc 120^o dựng trên đoạn AC

C. Hai cung chứa góc 60^o dựng trên đoạn AB

D. Hai cung chứa góc 115^o dựng trên đoạn BC

Lời giải:

Quỹ tích của điểm D là hai cung chứa góc 120^o dựng trên đoạn BC

Đáp án cần chọn là: A

Câu 7: Cho nửa đường tròn đường kính AB. Gọi M là điểm chính giữa của cung AB. Trên cung AM lấy điểm N. Trên tia đối của tia MA lấy điểm D sao cho MD = MB, trên tia đối của tia NB lấy điểm E sao cho NA = NE, trên tia đối của tia MB lấy điểm C sao cho MC = MA. Các điểm nào dưới đây cùng thuộc một đường tròn?

A. A, B, C, M, E                               

B. M, B, C, D, N

C. A, B, C, D, E                                

D. A, B, C, D, N

Lời giải:

Các tam giác ∆ANE, ∆AMC, ∆BMD lần lượt vuông cân tại N, M, M nên:

Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn

Đáp án cần chọn là: C

Câu 8: Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích của điểm M khi E di động trên cạnh BC

A. Nửa đường tròn đường kính BD

B. Cung BC của đường tròn đường kính BD

C. Cung BC của đường tròn đường kính BD trừ điểm B, C

D. Đường tròn đường kính BD

Lời giải:

Hay 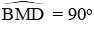 nên M thuộc đường tròn đường kính BD mà E  BC nên quỹ tích của điểm M là cung  BC của đường tròn đường kính BD

Đáp án cần chọn là: B

Câu 9: Cho tam giác ABC vuông tại A, có cạnh BC cố định. Gọi M là tâm đường tròn nội tiếp tam giác ABC. Tìm quỹ tích điểm M khi A di động.

A. Quỹ tích điểm M là hai cung chứa góc 120^o dựng trên BC

B. Quỹ tích điểm M là hai cung chứa góc 135^o dựng trên BC

C. Quỹ tích điểm M là hai cung chứa góc 115^o dựng trên BC

D. Quỹ tích điểm M là hai cung chứa góc 90^o dựng trên BC

Lời giải:

Tam giác ABC có: 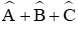 = 180^o (tính chất tổng 3 góc trong tam giác)

Vì M là tâm đường tròn nội tiếp tam giác nên BM, CM là phân giác của các góc 

 Quỹ tích điểm M là hai cung chứa góc 135^o dựng trên BC

Đáp án cần chọn là: B

Câu 10: Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo của hình thoi đó.

A. Quỹ tích điểm O là hai cung chứa góc 120^o dựng trên AB.

B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B

C. Quỹ tích điểm O là hai cung chứa góc 60^o dựng trên AB.

D. Quỹ tích điểm O là hai cung chứa góc 30^o dựng trên AB.

Lời giải:

Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường

⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B

Đáp án cần chọn là: B

Câu 11: Cho các hình vuông ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo của hình vuông đó.

A. Quỹ tích điểm O là hai cung chứa góc 120^o dựng trên AB.

B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B

C. Quỹ tích điểm O là hai cung chứa góc 60^o dựng trên AB.

D. Quỹ tích điểm O là hai cung chứa góc 30^o dựng trên AB.

Lời giải:

Xét hình vuông ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường

⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B

Đáp án cần chọn là: B

Câu 12: Cho tam giác đều ABC. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho MA² = MB² + MC²

A. Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên BC, trừ hai điểm B và C.

B. Quỹ tích điểm M là đường tròn đường kính BC

C. Quỹ tích điểm M là đường tròn đường kính BC, trừ hai điểm B và C.

D. Quỹ tích điểm M là 2 cung chứa góc 150^o dựng trên BC

Lời giải:

Vẽ tam giác BMN đều (N khác phía C đối với BM)

Xét ∆BNA và ∆BMC có:

BN = BM (vì tam giác BMN đều)

BA = BC (Vì tam giác ABC đều)

Suy ra ∆BNA = ∆BMC (c.g.c) nên ta có NA = MC

Ta có MA² = MB² + MC² = MN² + NA² nên 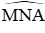 = 90^o

B,C cố định ⇒ Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên BC, trừ hai điểm B và C.

Đáp án cần chọn là: A

Câu 13: Cho tam giác đều ABC. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho MB² = MA² + MC²

A. Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên BC, trừ hai điểm B và C.

B. Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên AC, trừ hai điểm A và C.

C. Quỹ tích điểm M là đường tròn đường kính BC, trừ hai điểm B và C.

D. Quỹ tích điểm M là 2 cung chứa góc 150^o dựng trên AC

Lời giải:

Vẽ tam giác AMN đều (N khác phía C đối với AM)

Xét ∆BNA và ∆AMC có:

AN = AM (vì tam giác AMN đều)

BA = BC (Vì tam giác ABC đều)

Suy ra ∆ANB = ∆AMC (c.g.c) nên ta có NB = MC

Ta có MB² = MA² + MC² = MN² + NB² nên 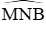 = 90^o

B, C cố định ⇒ Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên AC, trừ hai điểm A và C.

Đáp án cần chọn là: B

Câu 14: Cho tam giác ABC vuông cân tại A. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho 2MA² = MB² − MC²

A. Quỹ tích điểm M là hai cung chứa góc 135^o dựng trên AC, trừ hai điểm A và C.

B. Quỹ tích điểm M là đường tròn đường kính AC

C. Quỹ tích điểm M là đường tròn đường kính AC, trừ hai điểm A và C.

D. Quỹ tích điểm M là cung chứa góc 135^o dựng trên AC

Lời giải:

Vẽ tam giác MAD vuông cân tại A (M và D khác phía đối với AC)

Xét ∆BAM và ∆CAD có:

AM = AD (vì tam giác MAD vuông cân tại A)

BA = AC (Vì tam giác ABC vuông cân tại A )

Suy ra ∆BAM = ∆CAD (c.g.c) nên ta có BM = CD

⇒ Quỹ tích điểm M là hai cung chứa góc 135^o dựng trên AC, trừ hai điểm A và C.

Đáp án cần chọn là: A

Câu 15: Cho tam giác ABC vuông cân tại B. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho 2MB² = MA² − MC²

A. Quỹ tích điểm M là cung chứa góc 135^o dựng trên BC

B. Quỹ tích điểm M là đường tròn đường kính BC

C. Quỹ tích điểm M là đường tròn đường kính BC, trừ hai điểm B và C.

D. Quỹ tích điểm M là cung chứa góc 135^o dựng trên BC, trừ hai điểm B và C

Lời giải:

Vẽ tam giác MBD vuông cân tại B (M và D khác phía đối với BC)

Xét ∆ABM và ∆CBD có:

BM = BD (vì tam giác MBD vuông cân tại B)

BA = BC (Vì tam giác ABC vuông cân tại B)

Suy ra ∆ABM = ∆CBD (c.g.c) nên ta có AM = CD

Mà B,C cố định ⇒ Quỹ tích điểm M là cung chứa góc 135^o dựng trên BC, trừ hai điểm B và C.

Đáp án cần chọn là: D

Câu 16: Cho hình bình hành ABCD, hai đường chéo cắt nhau tại I. Từ A kẻ các đường vuông góc với BC, CD, DB thứ tự tại H, E, K. Xét các khẳng định sau:

I. Bốn điểm A, H, C, E nằm trên một đường tròn

II. Bốn điểm A, K, D, E nằm trên một đường tròn

III. Bốn điểm A, H, K, B nằm trên một đường tròn

IV. Bốn điểm K, I, E, H nằm trên một đường tròn

Chọn khẳng định đúng

A. Cả bốn khẳng định đều sai            

B. Cả bốn khẳng định đều đúng

C. Có ít nhất một khẳng định sai        

D. Có nhiều nhất một khẳng định sai

Lời giải:

AH ⊥ BC, AE ⊥ CD ⇒ bốn điểm A, H, C, E nằm trên đường tròn đường kính AC, I là trung điểm của AC

Lại có AH ⊥ BC, AK ⊥ BD, AE ⊥ CD nên bốn đỉnh A, K, E, D nằm trên đường tròn đường kính AD và bốn đỉnh A; K; H; B nằm trên đường tròn đường kính AB

Suy ra K và I cùng nhìn đoạn HE dưới một góc 2(180^o − )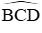

Vậy K, I, E, H nằm trên một đường tròn

Đáp án cần chọn là: B

Câu 17: Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB. Quỹ tích các điểm I là:

A. Quỹ tích điểm I là 2 cung chứa góc 30^o dựng trên AB

B. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 2

C. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 1/2

D. Quỹ tích điểm I là 2 cung chứa góc 60^o dựng trên AB

Lời giải:

Tam giác AMB vuông tại M, ta có 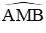 = 90^o. Mặt khác ta có

Mà A, B cố định ⇒ Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 1/2

Đáp án cần chọn là: C

Câu 18: Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 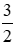 MB. Quỹ tích các điểm I là:

A. Quỹ tích điểm I là 2 cung chứa góc 45^o dựng trên AB

B. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 2

C. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 

D. Quỹ tích điểm I là 2 cung chứa góc 60^o dựng trên AB với tan a = 

Lời giải:

Tam giác AMB vuông tại M, ta có 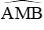 = 90^o. Mặt khác ta có

Mà A, B cố định ⇒ Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 

Đáp án cần chọn là: D

Câu 19: Cho tam giác ABC, gọi I là tâm đường tròn nội tiếp tam giác, P là một điểm trong tam giác thỏa mãn 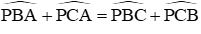. Xét các khẳng định sau:

I. P nhìn đoạn BC dưới một góc 90^o +  

II. I nhìn đoạn BC dưới một góc 90^o + 

Kết luận nào sau đây đúng?

A. Cả hai khẳng định đều sai             

B. Cả hai khẳng định đều đúng

C. Chỉ có I đúng và II sai                   

D. Chỉ có I sai và II đúng

Lời giải:

Suy ra P và I luôn nhìn đoạn BC về cùng một phía dưới cùng một góc 

Đáp án cần chọn là: B

Câu 20: Cho tam giác ABC cân tại A, M là điểm trên cạnh đáy BC. Qua M kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại D và E. Gọi N là điểm đối xứng của M qua DE. Quỹ tích các điểm N là:

A. Quỹ tích các điểm N là cung chứa góc bằng 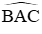 dựng trên đoạn BC

B. Quỹ tích các điểm N là cung chứa góc bằng 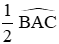 dựng trên đoạn BC

C. Quỹ tích các điểm N là cung chứa góc bằng 2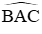 dựng trên đoạn BC

D. Quỹ tích các điểm N là cung chứa góc bằng 180^o − 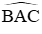 dựng trên đoạn BC

Lời giải:

(góc nội tiếp bằng nửa góc ở tâm cùng chắn cung BM)

Tương tự, E là tâm đường tròn ngoại tiếp tam giác CMN

Suy ra N nhìn đoạn BC dưới một góc bằng 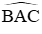 không đổi

Nên quỹ tích các điểm N là cung chứa góc bằng 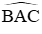 dựng trên đoạn BC

Đáp án cần chọn là: A

Câu 21: Cho tứ giác ABCD có 2 đường chéo vuông góc với nhau tại O.Biết 2 điểm A và B cố định, 2 điểm C và D di chuyển. Tìm quỹ tích điểm O

A. Đường tròn đường kính AB.

B. Đường tròn bán kính AB.

C. Đường tròn bán kính AB/2

D. Đường tròn đường kính 2AB

Lời giải:

Ta có: AC vuông góc BD tại O nên: 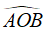 = 90°

Suy ra: quỹ tích điểm O là đường tròn đường kính AB

Đáp án cần chọn là:A

Câu 22: Cho đoạn thẳng BC cố định. Lấy điểm A bất kì sao cho tam giác ABC cân tại

A. Tìm quỹ tích điểm A?

A. Đường tròn tâm B bán kính BC.

B. Đường tròn tâm C bán kính BC.

C. Đường trung trực của đoạn thẳng BC.

D. Đường tròn đường kính BC.

Lời giải:

Do tam giác ABC cân tại A nên AB = AC

Suy ra, A thuộc đường trung trực của đoạn thẳng BC

Đáp án cần chọn là:C

Câu 23: Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại A.

Gọi M và N lần lượt là trung điểm BC và A

C. Tìm quỹ tích điểm N .

A. Đường tròn đường kính MC

B. Đường tròn đường kính BC

C. Đường tròn đường kính BM.

D. Đáp án khác

Lời giải:

Xét tam giác ABC có M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC

Suy ra: MN// AB

Lại có: AB ⊥ AC ⇒ MN ⊥ AC

Suy ra: 

Vì B và C cố định nên trung điểm M của BC cũng cố định

Do đó, quỹ tích các điểm N là đường tròn đường kính MC.

Đáp án cần chọn là:A

Câu 24: Cho hai điểm B và C cố định. Lấy A là điểm bất kì sao cho tam giác ABC cân tại

A. Gọi H là trực tâm của tam giác AB

C. Tìm quỹ tích điểm H

A. Đường tròn đường kính BC

B. Đường trung trực của đoạn thẳng BC

C. Đường tròn tâm B, bán kính BC

D. Đường tròn tâm C, bán kính BC

Lời giải:

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC

Lại có tam giác ABC là tam giác cân tại A nên đường cao AH đồng thời là đường trung trực.

Suy ra: H nằm trên đường trung trực của đoạn thẳng BC.

Đáp án cần chọn là:B

Lời giải:

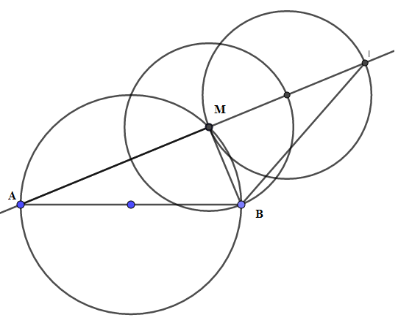
Tam giác $AMB$ vuông tại$M$ , ta có $\widehat{AMB}={90}^0$. Mặt khác ta có: $\widehat{AMB}+\widehat{IMB}={180}^0,$ suy ra $\widehat{IMB}={90}^0$

hay tam giác $BMI$ vuông tại $M$ . Trong tam giác vuông $BMI$ ta có $\tan \widehat{MIB}={\displaystyle \frac{MB}{MI}}={\displaystyle \frac{1}{2}}$

Suy ra $\widehat{MIB}=a^0$ không đổi hay $\widehat{AIB}=a^0$ không đổi. Mà $A,B$ cố định

$\Rightarrow$ Quỹ tích điểm $I$ là $2$  cung chứa góc $a^0$ dựng trên $AB$ với $\tan a={\displaystyle \frac{1}{2}}.$

Đáp án cần chọn là:C

Lời giải:

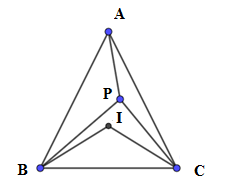
Theo giả thiết ta có:$\widehat{PBA}+\widehat{PCA}=\widehat{PBC}+\widehat{PCB}\Rightarrow \widehat{PBA}+\widehat{PCA}+\widehat{PBC}+\widehat{PCB}=2\left(\widehat{PBC}+\widehat{PCB}\right)$

$\Rightarrow 2\left(\widehat{PBC}+\widehat{PCB}\right)=\hat{B}+\hat{C}\Rightarrow 2\left({180}^0-\widehat{BPC}\right)=\hat{B}+\hat{C}={180}^0-\widehat{BAC}$$\Rightarrow \widehat{BPC}={90}^0+{\displaystyle \frac{1}{2}}\widehat{BAC}$

Mặt khác $\widehat{BIC}={180}^0-\left(\widehat{IBC}+\widehat{ICB}\right)={180}^0-{\displaystyle \frac{1}{2}}\left(\widehat{ABC}+\widehat{ACB}\right)$

$={180}^0-{\displaystyle \frac{1}{2}}\left({180}^0-\widehat{BAC}\right)={90}^0+{\displaystyle \frac{1}{2}}\widehat{BAC}$

Suy ra $P$ và $I$ luôn nhìn đoạn $BC$ về cùng một phía dưới cùng một góc ${90}^0+{\displaystyle \frac{1}{2}}\widehat{BAC}$.

Đáp án cần chọn là:B

Lời giải:

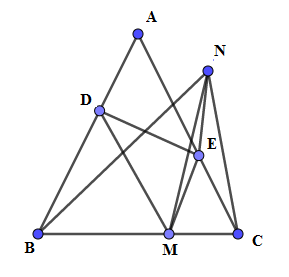
Ta có $MD//AC,ME//AB$

$\Rightarrow \widehat{BDM}=\hat{A}=\widehat{MEC}$

$\Rightarrow DB=DM,EC=EM.$

$M,N$ đối xứng nhau qua $DE$

$\Rightarrow DN=DM;EM=EN.$

$\Rightarrow$ $D$ là tâm đường tròn ngoại tiếp tam giác $BMN$

$\Rightarrow \widehat{BNM}={\displaystyle \frac{1}{2}}\widehat{BDM}={\displaystyle \frac{1}{2}}\hat{A}$ (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung $BM$ ).

Tương tự, $E$ là tâm đường tròn ngoại tiếp tam giác $CMN$ .

$\Rightarrow \widehat{MNC}={\displaystyle \frac{1}{2}}\widehat{MEC}={\displaystyle \frac{1}{2}}\hat{A}$ $\Rightarrow \widehat{BNC}=\widehat{BNM}+\widehat{MNC}=\hat{A}$

Suy ra $N$ nhìn đoạn $BC$ dưới một góc bằng $\widehat{BAC}$ không đổi.

Nên quỹ tích các điểm $N$ là  cung chứa góc bằng $\widehat{BAC}$  dựng trên đoạn $BC$ .

Đáp án cần chọn là:A

Lời giải:

Vì $C{A}^2+C{B}^2=100=A{B}^2$ nên $\mathrm{\Delta }ABC$ là tam giác vuông tại $C$ hay điểm $C$ luôn nhìn đoạn $AB$ một góc ${90}^0$.

Do đó quỹ tích các điểm $C$ là đường tròn đường kính $AB=10cm$ hay đường tròn tâm $M$ bán kính $5cm$.

Đáp án cần chọn là:C

Câu 29: Cho tam giác ABC nội tiếp đường tròn (O,R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau:

(I): O nằm trên cung tròn nhìn về một phía của BC dưới góc ${120}^{\circ }$.

(II): I nằm trên cung tròn nhìn về một phía của BC dưới góc ${120}^{\circ }$.

(III): H trên cung tròn nhìn về một phía của BC dưới góc ${120}^{\circ }$.

A.Cả ba khẳng định trên đều đúng.

B.Cả ba khẳng định trên đều sai.

C.Chỉ khẳng định I đúng.

D.Có ít nhất 1 khẳng định sai.

Lời giải:

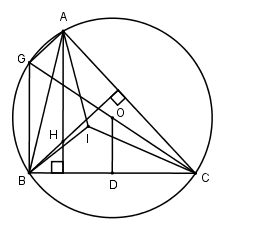
Gọi D là trung điểm của BC. Suy ra  $OD\mathrm{\perp }BC$.

Kéo dài OC cắt đường tròn tại điểm G ta có : $\widehat{CBG}={90}^0\Rightarrow BG\mathrm{\perp }BC\Rightarrow BG//AH$

$\Rightarrow OD={\displaystyle \frac{1}{2}}BG$ (tính chất đường trung bình).

Ta có: $\widehat{CAG}={90}^0\Rightarrow AG\mathrm{\perp }AC\iff AG//BH\Rightarrow$ AHBG là hình bình hành $\Rightarrow BG=AH\Rightarrow AH=2OD$ 

Theo giả thiết $AH=R\Rightarrow R=OB=2OD$

Tam giác OBD là tam giác vuông có $OB=2OD\Rightarrow \widehat{OBD}={30}^0$

$\Rightarrow \widehat{BOC}={120}^0\Rightarrow \widehat{BAC}={60}^0$

H là trực tâm của tam giác ABC$\Rightarrow CH\mathrm{\perp }AB,BH\mathrm{\perp }AC\Rightarrow \widehat{BHC}={120}^{\circ }.$

$\widehat{BIC}={180}^0-{\displaystyle \frac{1}{2}}\left(\widehat{ABC}+\widehat{ACB}\right)$$={180}^0-{\displaystyle \frac{1}{2}}\left({180}^0-\widehat{BAC}\right)={90}^0+{\displaystyle \frac{1}{2}}\widehat{BAC}={120}^0$

Ta thấy $\widehat{BOC}=\widehat{BHC}=\widehat{BIC}={120}^{\circ }$nên ba điểm O, H, I nằm trên cung tròn nhìn về một phía của BC dưới góc ${120}^0$.

Đáp án cần chọn là:A

Lời giải:

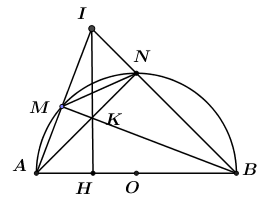
Gọi H là chân đường cao kẻ từ I đến cạnh AB.

Khi đó ta có: $S_{IAB}={\displaystyle \frac{1}{2}}IH.AB.$

Ta có AB là đường kính $\Rightarrow S_{IAB}Max\iff IHMax\iff$ H trùng với O.

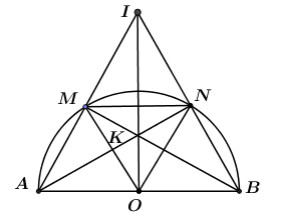
Khi H trùng với O thì OI vừa là đường cao vừa là đường trung tuyến của tam giác $\Rightarrow \mathrm{\Delta }IAB$ cân tại I.

Lại có ${\displaystyle \frac{MN}{AB}}={\displaystyle \frac{R}{2R}}={\displaystyle \frac{1}{2}}\Rightarrow MN$ là đường trung bình của tam giác $\mathrm{\Delta }ABC$.

$\Rightarrow MN//BC.$

Xét $\mathrm{\Delta }MON$ có $MO=ON=MN=R\Rightarrow \mathrm{\Delta }MON$ là tam giác đều.

Tam giác IAB cân tại I có MN là đường trung bình $\Rightarrow$ M và N lần lượt là trung điểm của AM và AB.

Lại có O là trung điểm của AB $\Rightarrow OM;ON$ cũng là hai đường trung bình của tam giác IAB.

$\Rightarrow \{\begin{array}{l}ON//IM\\ OM//IN\end{array}\Rightarrow$ tứ giác IMON là hình bình hành.

Lại có hai đường chéo OI và MN vuông góc với nhau $\left(doMN//AB;OI\mathrm{\perp }AB\right).$

$\Rightarrow IMON$ là hình thoi $\Rightarrow MI=IN=OM=R\Rightarrow IA=2IM=2R.$

Xét tam giác AOI vuông tại O ta có: $OI=\sqrt{I{A}^2-O{A}^2}=\sqrt{4R^2-R^2}=R\sqrt{3}.$

$\Rightarrow S_{IAB}={\displaystyle \frac{1}{2}}OI.AB={\displaystyle \frac{1}{2}}.R\sqrt{3}.2R=R^2\sqrt{3}.$

Đáp án cần chọn là:D