Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 1: Phương trình bậc nhất hai ẩn chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 1: Phương trình bậc nhất hai ẩn
Trả lời câu hỏi giữa bài:
b) Tìm thêm một nghiệm khác của phương trình
Phương pháp giải:
a) Cặp số là nghiệm của phương trình khi thỏa mãn hệ thức
b) Để tìm một nghiệm khác của phương trình ta cho nhận giá trị khác nghiệm tìm được ở câu a) rồi thay vào phương trình để tìm . Từ đó tìm được nghiệm của phương trình.
Lời giải:
a) + Cặp số là nghiệm của phương trình vì thay vào phương trình ta được (luôn đúng).
+ Cặp số là nghiệm của phương trình vì thay vào phương trình ta được (luôn đúng).
b) Chọn ta có:
Vậy cặp số là một nghiệm của phương trình
Phương pháp giải:
Chú ý rằng với mỗi x bất kì ta đều tìm được y thỏa mãn phương trình và ngược lại. Từ đó suy ra số nghiệm của phương trình.
Lời giải:
Vì với mỗi x bất kì ta đều tìm được y thỏa mãn phương trình và ngược lại.
Do đó, phương trình 2x – y = 1 có vô số nghiệm
|
x |
-1 |
0 |
0,5 |
1 |
2 |
2,5 |
|
y = 2x – 1 |
Lời giải:
|
x |
-1 |
0 |
0,5 |
1 |
2 |
2,5 |
|
y = 2x – 1 |
-3 |
-1 |
0 |
1 |
3 |
4 |
Vậy 6 nghiệm của phương trình là :
Bài tập trang 7 SGK Toán 9
a) ? b) ?
Phương pháp giải:
Cặp là nghiệm của phương trình nếu khi thay vào phương trình ta được hai vế bằng nhau.
Lời giải:
a) +) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
là nghiệm của phương trình .
Vậy có hai cặp số và là nghiệm của phương trình .
b) +) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
không là nghiệm của phương trình .
+) Xét cặp số . Thay vào phương trình ta được
là nghiệm của phương trình .
Vậy có hai cặp số và là nghiệm của phương trình .
Bài 2 trang 7 SGK Toán 9 tập 2: Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:a) b)
d)
e) f)
Phương pháp giải:
1) Tìm nghiệm tổng quát của phương trình:
+) Nếu thì tìm theo . Khi đó công thức nghiệm là:
+) Nếu thì tìm theo . Khi đó công thức nghiệm là:
2) Cách vẽ đường thẳng có phuương trình: .
+) Nếu thì vẽ đường thẳng
+) Nếu thì vẽ đường thẳng song song hoặc trùng với trục tung.
+) Nếu thì vẽ đường thẳng song song hoặc trùng với trục hoành.
Lời giải:
a) Ta có phương trình . Nghiệm tổng quát của phương trình là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Cho ta được .
Cho ta được .
Biểu diễn cặp điểm và trên hệ trục tọa độ và đường thẳng chính là tập nghiệm của phương trình .
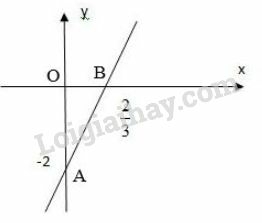
b)
Ta có phương trình . Nghiệm tổng quát của phương trình là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
+) Cho ta được .
+) Cho ta được .
Biểu diễn cặp điểm , trên hệ trục toa độ và đường thẳng chính là tập nghiệm của phương trình.
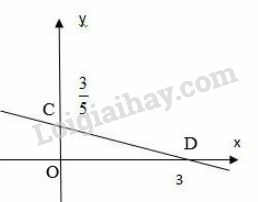
c) Ta có phương trình . Nghiệm tổng quát của phương trình là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình
+) Cho ta được
+) Cho ta được
Biểu diễn cặp điểm và trên hệ tọa độ và đường thẳng chính là tập nghiệm của phương trình .
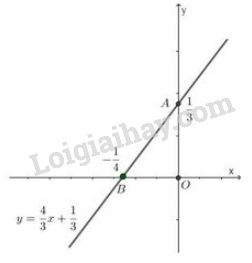
d)
Ta có phương trình . Nghiệm tổng quát của phương trình là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình
+) Cho ta được
+) Cho ta được .
Biểu diễn cặp điểm và trên hệ tọa độ và đường thẳng OA chính là tập nghiệm của phương trình .
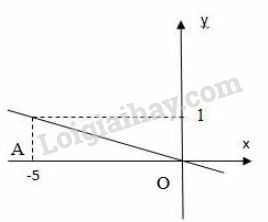
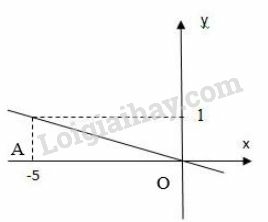
e)
Ta có phương trình . Nghiệm tổng quát của phương trình là:
Tập nghiệm là đường thẳng đi qua và song song với trục tung.
f)
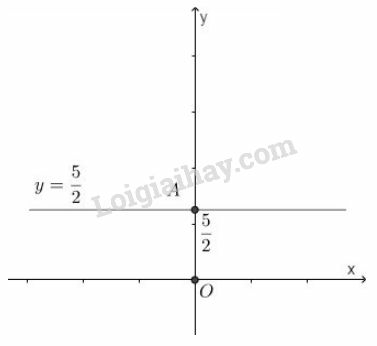
Nghiệm tổng quát của phương trình là:
Tập nghiệm là đường thẳng đi qua và song song với trục hoành
Phương pháp giải:
1) Cho phương trình: . Biến đổi .
+) Cho . Đường thẳng đi qua điểm
+) Cho . Đường thẳng đi qua điểm
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm .
2) Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình: . Giải phương trình tìm được thay vào một trong hai phương trình trên tìm được tung độ giao điểm.
Lời giải:
* Ta có: .
+ Cho ta được .
+ Cho ta được .
Đường thẳng cần vẽ là đường thẳng đi qua .
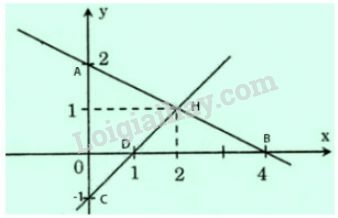
* Ta có: .
+ Cho ta được .
+ Cho ta được .
Đường thẳng cần vẽ là đường thẳng đi qua .
* Tìm giao điểm:
Hoành độ giao điểm là nghiệm của phương trình:
Vậy tọa độ giao điểm của hai đường thẳng trên là . Tọa độ của nó là nghiệm của cả hai phương trình đã cho.
Lý thuyết Bài 1: Phương trình bậc nhất hai ẩn
1. Các kiến thức cần nhớ
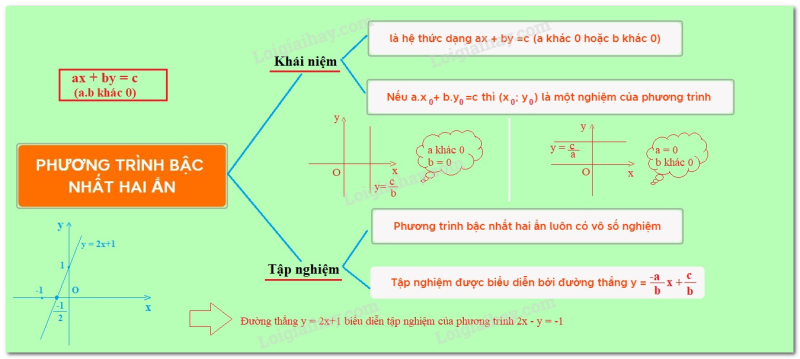
Khái niệm phương trình bậc nhất hai ẩn
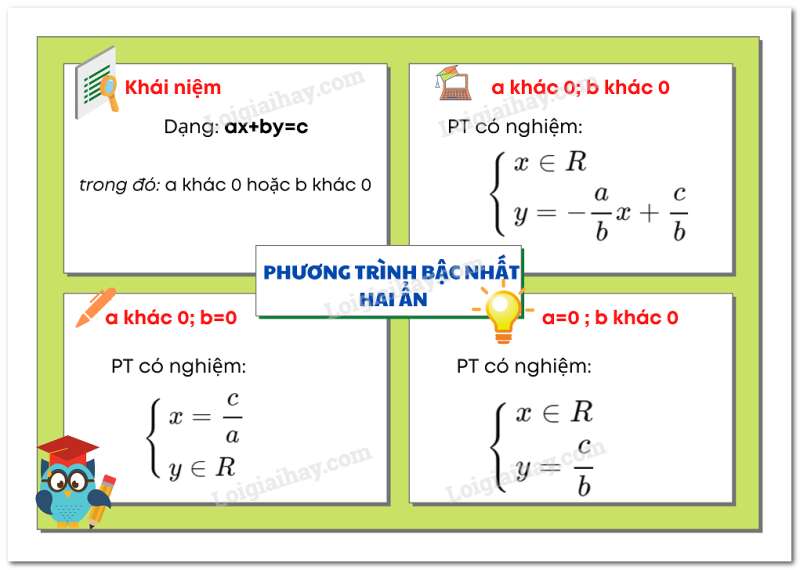
+) Phương trình bậc nhất hai ẩn là phương trình có dạng
Trong đó là những số cho trước hoặc .
- Nếu các số thực thỏa mãn thì cặp số được gọi là nghiệm của phương trình .
- Trong mặt phẳng tọa độ , mỗi nghiệm của phương trình được biểu diễn bới điểm có tọa độ .
Tập nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng
+) Nếu và thì phương trình có nghiệm
và đường thẳng song song hoặc trùng với trục tung.
+) Nếu và thì phương trình có nghiệm
và đường thẳng song song hoặc trùng với trục hoành.
+) Nếu và thì phương trình có nghiệm
và đường thẳng là đồ thị hàm số
2. Các dạng toán thường gặp
Dạng 1: Tìm điều kiện của tham số để một cặp số cho trước là nghiệm của phương trình bậc nhất hai ẩn.
Phương pháp:
Nếu cặp số thực thỏa mãn thì nó được gọi là nghiệm của phương trình .
Dạng 2: Viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn. Biểu diễn tập nghiệm trên hệ trục tọa độ.
Phương pháp:
Xét phương trình bậc nhất hai ẩn .
1. Để viết công thức nghiệm tổng quát của phương trình, trước tiên ta biểu diễn theo ( hoặc theo ) rồi đưa ra công thức nghiệm tổng quát.
2. Để biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có phương trình .
Dạng 3: Tìm điều kiện của tham số để đường thẳng thỏa mãn điều kiện cho trước
Phương pháp:
Ta có thể sử dụng một số lưu ý sau đây khi giải dạng toán này:
1. Nếu và thì phương trình đường thẳng có dạng . Khi đó song song hoặc trùng với .
2. Nếu và thì phương trình đường thẳng có dạng . Khi đó song song hoặc trùng với .
3. Đường thẳng đi qua điểm khi và chỉ khi .
Dạng 4: Tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn
Phương pháp:
Để tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn , ta làm như sau:
Cách 1:
Bước 1: Rút gọn phương trình, chú ý đến tính chia hết của các ẩn
Bước 2: Biểu thị ẩn mà hệ số của nó có giá trị tuyệt đối nhỏ (chẳng hạn ) theo ẩn kia.
Bước 3: Tách riêng giá trị nguyên ở biểu thức của
Bước 4: Đặt điều kiện để phân bố trong biểu thức của bằng một số nguyên , ta được một phương trình bậc nhất hai ẩn và
- Cứ tiếp tục như trên cho đến khi các ần đều được biểu thị dưới dạng một đa thức với các hệ số nguyên.
Cách 2:
Bước 1. Tìm một nghiệm nguyên của phương trình.
Bước 2. Đưa phương trình về dạng từ đó dễ dàng tìm được các nghiệm nguyên của phương trình đã cho.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.