Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 1. Phương trình bậc nhất hai ẩn trang 5,6,7,8 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 1. Phương trình bậc nhất hai ẩn
Phần câu hỏi bài 1 trang 5, 6 Vở bài tập toán 9 tập 2
Câu 1
Phương trình bậc nhất hai ẩn là hệ thức dạng ax + by = c, trong đó a, b và c là:
(A) ba số đã cho tùy ý
(B) Ba số đã cho thỏa mãn điều kiện và và
(C) Ba số đã cho thỏa mãn điều kiện hoặc hoặc
(D) Ba số đã cho thỏa mãn điều kiện hoặc hoặc c tùy ý.
Phương pháp giải:
Sử dụng định nghĩa phương trình bậc nhất hai ẩn
Lời giải chi tiết:
Phương trình bậc nhất hai ẩn là phương trình có dạng , trong đó là những số cho trước a≠0 hoặc b≠0.
Chọn D.
Câu 2
Phương trình bậc nhất hai ẩn 0x – y = 2 có tập nghiệm là:
(A)
(B)
(C)
(D)
Khoanh tròn vào chữ cái trước đáp án đúng.
Phương pháp giải:
Tập nghiệm của phương trình bậc nhất hai ẩn :
Nếu a=0 và b≠0 thì phương trình có nghiệm , ta có thể viết
Trả lời:
Ta có
Tập nghiệm của phương trình là
Chọn C.
Câu 3
Xét bốn phương trình bậc nhất hai ẩn:
0x + 4y = 8 (1) ; 2x – 3y = -6 (2); 3x – 2y = -6 (3) ; 2x + 0y = 4 (4)
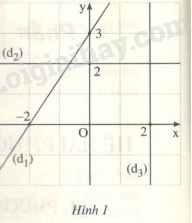
Với mỗi đường thẳng (d1), (d2) và (d3) cho bởi hình 1, hãy tìm một phương trình rồi ghép thành cặp sao cho trong mỗi cặp, tập nghiệm của phương trình được biểu diễn bởi đường thẳng cùng cặp với nó.
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
Nên để tìm phương trình ghép cặp được với đường thẳng cho trước ta có thể tìm nghiệm tổng quát của mỗi phương trình rồi xét xem nó tương ứng với đường thẳng nào trên hình vẽ.
Trả lời:
nên tập nghiệm của phương trình được biểu diễn bởi đường thẳng song song với trục Nhận thấy trên hình vẽ có đường thẳng song song với trục hoành và đi qua điểm nên ta ghép với phương trình
nên tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm . Nhận thấy không có đường thẳng nào trên hình vẽ thỏa mãn.
nên tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm . Nhận thấy đường thẳng thỏa mãn nên ta ghép cặp và phương trình
nên tập nghiệm phương trình được biểu diễn bởi đường thẳng đi qua
và song song với trục tung. Nhận thấy đường thẳng thỏa mãn nên ta ghép cặp và phương trình
.
Trong các cặp số cặp số nào là nghiệm của phương trình:
LG a
Phương pháp giải:
Nếu cặp số thực thỏa mãn thì nó được gọi là nghiệm của phương trình .
Trả lời:
Xét phương trình
Cặp số không phải nghiệm của phương trình vì
Cặp số là nghiệm của phương trình vì
Cặp số không phải nghiệm của phương trình vì
Cặp số không phải nghiệm của phương trình vì
Cặp số là nghiệm của phương trình vì
LG b
Phương pháp giải:
Nếu cặp số thực thỏa mãn thì nó được gọi là nghiệm của phương trình .
Trả lời:
Xét phương trình
Cặp số không phải nghiệm của phương trình vì
Cặp số không phải nghiệm của phương trình vì
Cặp số là nghiệm của phương trình vì
Cặp số không phải nghiệm của phương trình vì
Cặp số (4;-3) là nghiệm của phương trình vì 3.4+5.(-3) =-3
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
LG a
3x – y =2
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
+) Nếu a≠0 và b=0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm và đường thẳng d là đồ thị hàm số
Trả lời:
Ta có
Vậy nghiệm tổng quát của phương trình là với .
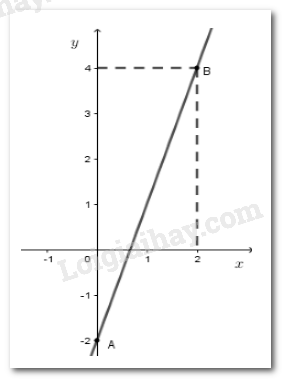
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm và .
Vẽ hình 2:
LG b
x + 5y = 3
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
+) Nếu a≠0 và b=0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm và đường thẳng d là đồ thị hàm số
Trả lời:
Ta có
Vậy nghiệm tổng quát của phương trình là với .
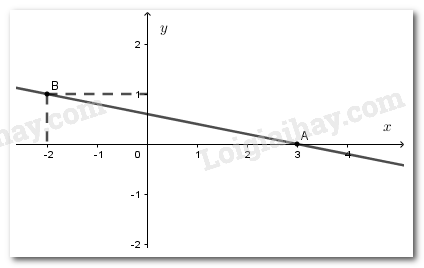
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm và .
Vẽ hình 3:
LG c
4x – 3y = -1
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
+) Nếu a≠0 và b=0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm và đường thẳng d là đồ thị hàm số
Trả lời:
Ta có
Vậy nghiệm tổng quát của phương trình là với .
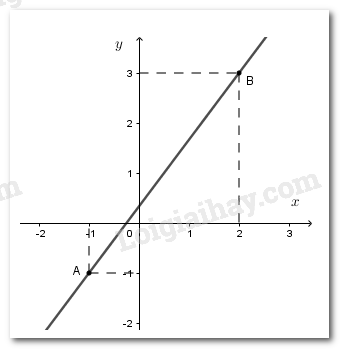
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm và .
Vẽ hình 4:
LG d
0x + 2y = 5
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
+) Nếu a≠0 và b=0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm và đường thẳng d là đồ thị hàm số
Trả lời:
Ta có
Vậy nghiệm tổng quát của phương trình là với .
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm và .
Vẽ hình 5:
Cho hai phương trình và Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của những phương trình nào ?
Phương pháp giải:
Tập nghiệm của phương trình biểu diễn bởi đường thẳng
Có thể vẽ đường thẳng bằng cách vẽ đường thẳng đi qua hai điểm và với
Vẽ các đường thẳng biểu diễn tập nghiệm của các phương trình đã cho. Sau đó xác định tọa độ giao điểm của hai đường thẳng.
Trả lời:
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm và
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng đi qua hai điểm và
Vẽ hình 6:
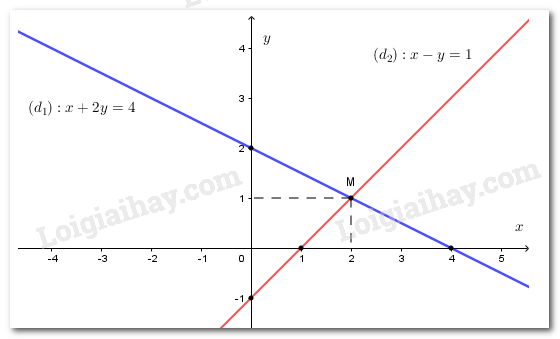
Trên hình 6 ta thấy và cắt nhau tại
Tọa độ của điểm thỏa mãn phương trình vì khi thay và vào vế trái, ta có
Tọa độ của điểm thỏa mãn phương trình vì khi thay và vào vế trái, ta có
Chú ý:
Sai lầm dễ mắc phải là học sinh vẽ các đường thẳng không chính xác, dẫn đến xác định sai tọa độ giao điểm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.