Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 2. Hệ hai phương trình bậc nhất hai ẩn trang 9,10,11,12,13 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
Nội dung bài viết
VBT Toán lớp 9 Bài 2. Hệ hai phương trình bậc nhất hai ẩn
Phần câu hỏi bài 2 trang 9, 10 Vở bài tập toán 9 tập 2
Câu 4
Cho hệ phương trình {2x=−43y+6=0
(A) Hệ phương trình đã cho có một nghiệm là x = -2
(B) Hệ phương trình đã cho có hai nghiệm là x = -2 và y = -2
(C) Hệ phương trình đã cho có nghiệm duy nhất là (x ; y) = (-2 ; -2)
(D) Hệ phương trình đã cho vô nghiệm
Phương pháp giải:
Sử dụng lý thuyết về nghiệm của hệ hai phương trình bậc nhất hai ẩn {ax+by=c(1)a′x+b′y=c′(2)
Giải phương trình (1) và phương trình (2) sau đó tìm nghiệm của hệ phương trình đã cho.
Trả lời:
Ta có {2x=−43y+6=0⇔{x=−23y=−6⇔{x=−2y=−2
Vậy hệ phương trình đã cho có nghiệm duy nhất là (x;y)=(−2;−2)
Chọn C.
Câu 5
Cho hai hệ phương trình
(I){x=y−1y=x+1 và (II){2x−3y=53y+5=2x
(A) Hệ (I) có vô số nghiệm và hệ (II) vô nghiệm
(B) Hệ (I) vô nghiệm và hệ (II) có vô số nghiệm
(C) Hệ (I) vô nghiệm và hệ (II) vô nghiệm
(D) Hệ (I) có vô số nghiệm và hệ (II) có vô số nghiệm
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Xét hệ (I):{x=y−1y=x+1⇔{y=x+1y=x+1 .
Nhận thấy rằng hai đường thẳng (d1):y=x+1 và (d2):y=x+1 trùng nhau nên hệ (I) có vô số nghiệm.
Xét hệ (II){2x−3y=53y+5=2x⇔{3y=2x−53y=2x−5⇔{y=23x−53y=23x−53
Nhận thấy rằng hai đường thẳng (d3):y=23x−53 và (d4):y=23x−53 trùng nhau nên hệ (II) có vô số nghiệm.
Vậy cả hai hệ đã cho đều có vô số nghiệm.
Chọn B.
Câu 6
Cho một hệ hai phương trình bậc nhất hai ẩn. Tập nghiệm của phương trình thứ nhất trong hệ được biểu diễn bởi đường thẳng (d1); Tập nghiệm của phương trình thứ hai trong hệ được biểu diễn bởi đường thẳng (d2). Hãy ghép mỗi cụm từ nằm ở cột trái với mỗi cụm từ nằm ở cột phải để được khẳng định đúng:
|
a) Nếu (d1) cắt (d2) tại một điểm thì b) Nếu (d1) song song (d2) thì c) Nếu (d1) trùng với (d2) thì |
1) Hệ phương trình đã cho có một nghiệm duy nhất 2) Hệ phương trình đã cho có tập nghiệm trùng với tập nghiệm của một trong hai phương trình trong hệ 3) Hệ phương trình đã cho vô nghiệm 4) Hệ phương trình đã cho có vô số nghiệm và mỗi cặp số (p ; q) tùy ý đều là một nghiệm của hệ. |
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Nếu (d1) cắt (d2) tại một điểm thì hệ phương trình đã cho có nghiệm duy nhất.
Nếu (d1) song song (d2) thì hệ phương trình đã cho vô nghiệm.
Nếu (d1) trùng (d2) thì hệ phương trình đã cho có vô số nghiệm. Tập nghiệm của hệ trùng với tập nghiệm của một trong hai phương trình trong hệ.
Như vậy ta có thứ tự nối đúng là a−1;b−3;c−2.
Không cần vẽ hình, hãy cho biết nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
Chú ý: Trong bài tập này, ta cần xét vị trí tương đối của hai đường thẳng (để suy ra số nghiệm của hệ phương trình mà không cần vẽ hai đường thẳng đó. Muốn vậy, ta phải dựa vào hệ số góc và tung độ gốc đối của chúng).
LG a
{y=3−2xy=3x−1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Đường thẳng y=3−2x có hệ số góc là −2
Đường thẳng y=3x−1 có hệ số góc là 3
Vì hai đường thẳng có hệ số góc khác nhau nên chúng cắt nhau tại một điểm.
Do đó, hệ phương trình có nghiệm duy nhất.
LG b
{y=−12x+3y=−12x+1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Đường thẳng y=−12x+3 có hệ số góc là −12 và tung độ gốc là 3.
Đường thẳng y=−12x+1 có hệ số góc là −12 và tung độ gốc là 1.
Vì hai đường thẳng có hệ số góc bằng nhau nhưng có tung độ gốc khác nhau nên chúng song song.
Vậy hệ phương trình vô nghiệm.
LG c
{2y=−3x3y=2x
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Ta có {2y=−3x3y=2x⇔{y=−32xy=23x
Đường thẳng y=−32x có hệ số góc là −32
Đường thẳng y=23x có hệ số góc là 23
Vì hai đường thẳng có hệ số góc khác nhau nên chúng cắt nhau tại một điểm.
Do đó, hệ phương trình có nghiệm duy nhất.
LG d
{3x−y=3x−13y=1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Ta có {3x−y=3x−13y=1⇔{y=3x−3y=3x−3
Hai đường thẳng có phương trình đã cho trong hệ là y=3x−3 nên hệ phương trình đã cho có vô số nghiệm.
Đoán nhận số nghiệm của các hệ phương trình sau bằng hình học:
Chú ý: Trong bài này, ta cần xét vị trí tương đối của hai đường thẳng (để suy ra số nghiệm của hệ phương trình) bằng cách vẽ hai đường thẳng đó.
LG a
{2x−y=1x−2y=−1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó ta vẽ hai đường thẳng d và d′ trên cùng hệ trục tọa độ để xác định số giao điểm của d và d′ .
Từ đó suy ra số nghiệm của hệ đã cho.
Trả lời:
Vẽ các đường thẳng 2x−y=1;x−2y=−1 trong cùng một hệ tọa độ (h.7)
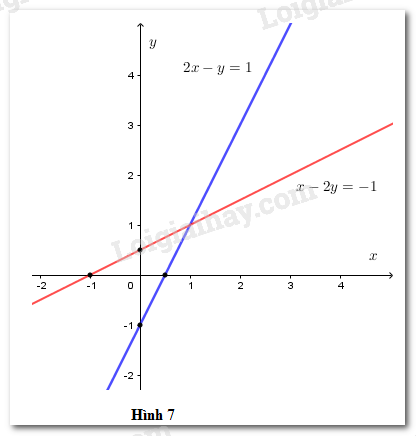
Ta thấy hai đường thẳng này cắt nhau tại một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
LG b
{2x+y=4−x+y=1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó ta vẽ hai đường thẳng d và d′ trên cùng hệ trục tọa độ để xác định số giao điểm của d và d′ .
Từ đó suy ra số nghiệm của hệ đã cho.
Trả lời:
Vẽ các đường thẳng 2x+y=4;−x+y=1 trong cùng một hệ tọa độ (h.8)
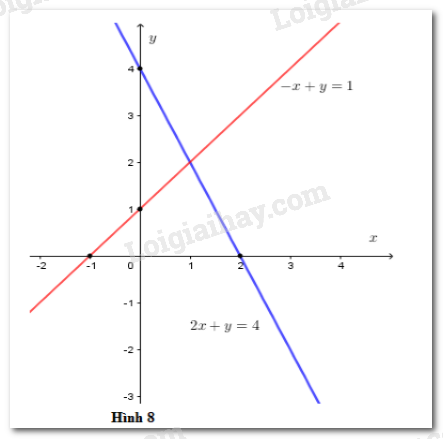
Ta thấy hai đường thẳng này cắt nhau tại một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5
LG a
Tìm nghiệm tổng quát của mỗi phương trình trên.
Phương pháp giải:
Sử dụng cách tìm nghiệm của phương trình bậc nhất hai ẩn ax+by=0(a,b≠0) để tìm nghiệm tổng quát của mỗi phương trình đã cho.
Trả lời:
Ta có 2x+y=4⇔y=−2x+4
Vậy nghiệm tổng quát của phương trình thứ nhất là (x;−2x+4) với x∈R.
Tương tự, 3x+2y=5⇔y=−32x+52
Vậy nghiệm tổng quát của phương trình thứ hai là (x;−32x+52) với x∈R.
LG b
Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ rồi xác định nghiệm chung của chúng.
Phương pháp giải:
Xác định tọa độ các điểm mà đường thẳng đi qua.
Vẽ các đường thẳng trên cùng hệ trục tọa độ để xác định nghiệm chung.
Trả lời:
Đường thẳng 2x+y=4 đi qua các điểm có tọa độ (2;0);(1;2)
Đường thẳng 3x+2y=5 đi qua các điểm có tọa độ (1;1);(−1;4)
Vẽ hai đường thẳng trong cùng hệ tọa độ (h.9)
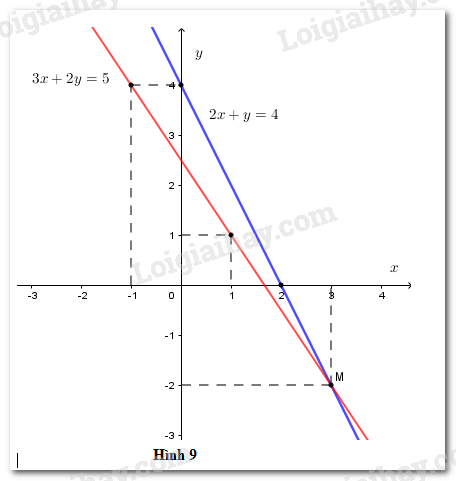
Hai đường thẳng cắt nhau tại M(3;−2)
Thử lại, ta thấy (3;−2) nghiệm đúng phương trình 2x+y=4 (vì 2.3+(−2)=4) và phương trình 3x+2y=5 (vì 3.3+2(−2)=5).
Vậy (3;−2) là nghiệm chung của hai phương trình đã cho.
Chú ý:
Nói chung, việc xác định tọa độ của M chỉ cho kết quả gần đúng. Do đó, để chắc chắn cặp số tìm được (tọa độ của điểm M) là nghiệm của phương trình thì ta phải thử trực tiếp vào phương trình.
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
LG a
{x+y=23x+3y=2
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Tập nghiệm của phương trình x+y=2 được biểu diễn bởi đường thẳng y=−x+2 có hệ số góc bằng −1, tung độ gốc bằng 2.
Tập nghiệm của phương trình 3x+3y=2 được biểu diễn bởi đường thẳng y=−x+23 có hệ số góc bằng −1, tung độ gốc bằng 23.
Hai đường thẳng này có hệ số góc bằng nhau nhưng tung độ gốc khác nhau nên chúng song song với nhau.
Vậy hệ phương trình đã cho vô nghiệm.
LG b
{3x−2y=1−6x+4y=0
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Tập nghiệm của phương trình 3x−2y=1 được biểu diễn bởi đường thẳng y=32x−12 có hệ số góc bằng 32, tung độ gốc bằng −12.
Tập nghiệm của phương trình −6x+4y=0 được biểu diễn bởi đường thẳng y=32x có hệ số góc bằng 32, tung độ gốc bằng 0.
Hai đường thẳng này có hệ số góc bằng nhau nhưng tung độ gốc khác nhau nên chúng song song với nhau.
Vậy hệ phương trình đã cho vô nghiệm.
Bài 8 trang 13 Vở bài tập toán 9 tập 2
LG a
{4x−4y=2−2x+2y=−1
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Tập nghiệm của phương trình 4x−4y=2 được biểu diễn bởi đường thẳng y=x−12 có hệ số góc bằng 1 và tung độ gốc bằng −12
Tập nghiệm của phương trình −2x+2y=−1 được biểu diễn bởi đường thẳng y=x−12 có hệ số góc bằng 1 và tung độ gốc bằng −12
Hai đường thẳng này có hệ số góc bằng nhau và tung độ gốc bằng nhau nên chúng trùng nhau.
Vậy hệ phương trình đã cho có vô số nghiệm.
LG b
{13x−y=23x−3y=2
Phương pháp giải:
Xét hệ phương trình {ax+by=c(1)a′x+b′y=c′(2) có d là đường thẳng biểu diễn tập nghiệm của phương trình (1) và d′ là đường thẳng biểu diễn tập nghiệm của phương trình (2), khi đó
Trường hợp 1. d∩d′=A(x0;y0)⇔ Hệ phương trình có nghiệm duy nhất (x0;y0);
Trường hợp 2. d//d′⇔ Hệ phương trình vô nghiệm;
Trường hợp 3. d≡d′⇔ Hệ phương trình có vô số nghiệm.
Trả lời:
Tập nghiệm của phương trình 13x−y=23 được biểu diễn bởi đường thẳng y=13x−23 có hệ số góc bằng 13, tung độ gốc bằng −23.
Tập nghiệm của phương trình x−3y=2 được biểu diễn bởi đường thẳng y=13x−23 có hệ số góc bằng 13, tung độ gốc bằng −23.
Hai đường thẳng này có hệ số góc bằng nhau và tung độ gốc bằng nhau nên chúng trùng nhau.
Vậy hệ phương trình đã cho có vô số nghiệm.
Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó ? Vì sao ?
Phương pháp giải:
Ta sử dụng nhận xét: nếu hệ phương trình bậc nhất hai ẩn có hai nghiệm trở lên thì hệ phương trình đó có vô số nghiệm.
Dựa vào việc minh họa hình học của tập nghiệm để lập luận suy ra lời giải đúng.
Trả lời:
Ta biết rằng tập nghiệm của một phương trình bậc nhất hai ẩn được biểu diễn bởi một đường thẳng. Do đó nếu hai nghiệm của hệ phương trình biểu diễn bởi hai điểm M và N phân biệt thì các đường thẳng biểu diễn tập nghiệm của mỗi phương trình trong hệ đều phải đi qua M và N. Điều đó có nghĩa là tập nghiệm của hệ phương trình đã cho cũng được biểu diễn bởi đường thẳng MN. Vậy hệ phương trình đã cho có vô số nghiệm.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.