Toán 10 Chân trời sáng tạo trang 40 Bài 1: Toạ độ vecto

Giang Ngày: 12-02-2023 Lớp 10

389

Với giải Câu hỏi trang 40 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 1: Toạ độ vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 40 Bài 1: Toạ độ vecto

Thực hành 1 trang 40 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm $D (- 1; 4), E (0; - 3), F (5; 0)$

a) Vẽ các điểm D, E, F trên mặt phẳng Oxy

b) Tìm tọa độ của các vectơ $\vec{O D}, \vec{O E}, \vec{O F}$ .

c) Vẽ và tìm tọa độ hai vectơ đơn vị và $\vec{j}$ lần lượt trên hai trục tọa độ Ox và Oy

Lời giải

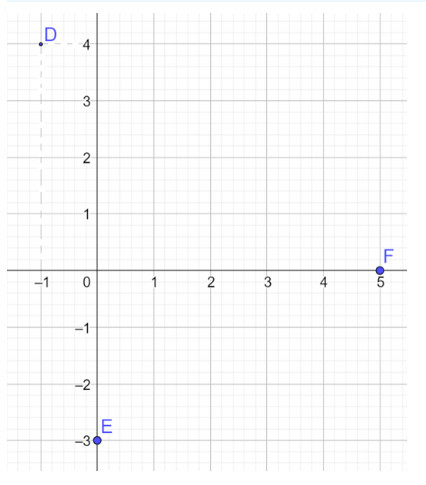
Thực hành 1 trang 40 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

b) Vì tọa độ vectơ $\vec{O M}$ chính là tọa độ của điểm M (với mọi M) nên ta có:

$\vec{O D} = (- 1; 4), \vec{O E} = (0; - 3), \vec{O F} = (5; 0)$

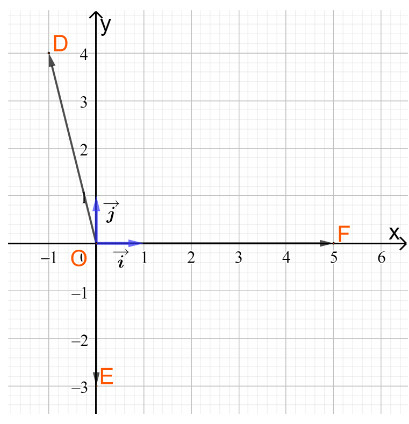
Thực hành 1 trang 40 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 2)

Từ hình vẽ ta có tọa độ của hai vectơ và $\vec{j}$ là

và $\vec{j} = (0; 1)$

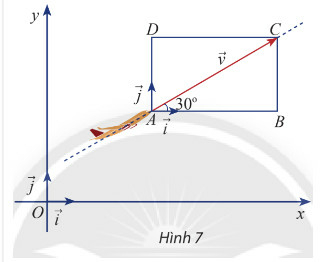
Vận dụng 1 trang 40 Toán 10 Tập 2: Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc $30^{\circ}$ (hình 7)

a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD

b) Biểu diễn vận tốc $\vec{v}$ theo hai vectơ và $\vec{j}$

c) Tìm tọa độ của $\vec{v}$

Vận dụng 1 trang 40 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

Lời giải

a) Vận tốc 240 km/h nên $| \vec{v} | = A C = 240$

Áp dụng các tính chất trong tam giác vuông ta có

$A B = D C = A C . \cos (\hat{C A B}) = 240. \cos (30^{\circ}) = 120 \frac{\sqrt{3}}{2}$

$A D = B C = A C . \sin (\hat{C A B}) = 240. \sin (30^{\circ}) = 120$

b) Xem A là gốc tọa độ nên ta có $\vec{A B} = 120 \vec{i}, \vec{A D} = 120 \frac{\sqrt{3}}{2} \vec{j}, \vec{v} = \vec{A C} = 120 \vec{i} + 120 \frac{\sqrt{3}}{2} \vec{j}$

Ta có $\vec{v} = 120 \vec{i} + 120 \frac{\sqrt{3}}{2} \vec{j}$

Vậy tọa độ của vectơ $\vec{v}$ là $(120; 120 \frac{\sqrt{3}}{2})$

2. Biểu thức tọa độ của các phép toán vecto

HĐ Khám phá 2 trang 40 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai vectơ $\vec{a} = (a_{1}, a_{2}), \vec{b} = (b_{1}, b_{2})$ và số thực k. Ta đã biết có thể biểu diễn từng vectơ $\vec{a}, \vec{b}$ theo hai vectơ , $\vec{j}$ như sau

a) Biểu diễn từng vectơ $\vec{a} + \vec{b}, \vec{a} - \vec{b}, k \vec{a}$ theo hai vectơ , $\vec{j}$

b) Tìm $\vec{a} . \vec{b}$ theo tọa độ của hai vectơ $\vec{a}$ và $\vec{b}$

Lời giải

a) Ta có

$\begin{array}{l} \vec{a} + \vec{b} = (a_{1} + a_{2} \vec{j}) + (b_{1} + b_{2} \vec{j}) = (a_{1} + b_{1}) + (a_{2} + b_{2}) \\ \vec{a} - \vec{b} = (a_{1} + a_{2} \vec{j}) - (b_{1} + b_{2} \vec{j}) = (a_{1} - b_{1}) + (a_{2} - b_{2}) \\ k \vec{a} = k (a_{1} + a_{2} \vec{j}) = k a_{1} + k a_{2} \vec{j} \end{array}$

b) Ta có

$\begin{array}{l} \vec{a} . \vec{b} = (a_{1} \vec{i} + a_{2} \vec{j}) . (b_{1} \vec{i} + b_{2} \vec{j}) \\ = a_{1} b_{1} {\vec{i}}^{2} + a_{1} b_{2} \vec{i} . \vec{j} + a_{2} b_{1} \vec{i} \vec{j} + a_{2} b_{2} {\vec{j}}^{2} \\ = a_{1} b_{1} + a_{2} b_{2} \end{array}$