Với giải Câu hỏi trang 38 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 1: Toạ độ vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Chân trời sáng tạo trang 41 Bài 1: Toạ độ vecto
Thực hành 2 trang 41 Toán 10 Tập 2: Cho hai vectơ →m=(−6;1),→n=(0;2)
a) Tìm tọa độ các vectơ →m+→n,→m−→n,10→m,−4→n
b) Tính các tích vô hướng →m.→n,(10→m).(−4→n)
Phương pháp giải:
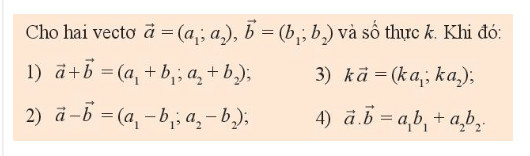
Lời giải
a) Ta có
→m+→n=((−6+0);1+2)=(−6;3)→m−→n=((−6−0);(1−2))=(−6;−1)10→m=(10.(−6);10.1)=(−60;10)−4→n=((−4).0;(−4).2)=(0;−8)
b) Ta có
→m.→n=(−6).0+1.2=0+2=2
Ta có 10→m=(−60;10) và −4→n=(0;−8) nên (10→m).(−4→n)=(−60).0+10.(−8)=0−80=−80
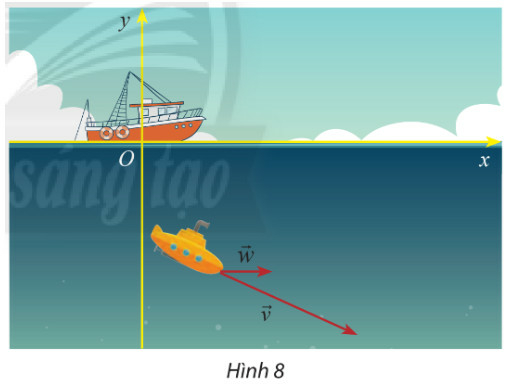
Phương pháp giải:
Với →v=(v1;v2),→w=(w1;w2) thì →v+→w là (v1+w1;v2+w2)
Lời giải
→v+→w=(10+3,5;(−8)+0)=(13,5;−8)
Vậy tọa độ của vectơ tổng hai vận tốc →v và →w là (13,5;−8)
3. Áp dụng của tọa độ vecto
Phương pháp giải:
Với →v=(v1;v2),→w=(w1;w2) thì →v+→w là (v1+w1;v2+w2)
Lời giải
Ta có tọa độ vectơ →OB,→OA chính là tọa độ điểm B và A
Nên ta có →OB=(xB;yB),→OA=(xA;yA)
→AB=→OB−→OA=(xB;yB)−(xA;yA)=(xB−xA;yB−yA)
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khởi động trang 38 Toán 10 Tập 2: Hãy tìm cách xác định vị trí các quân mã trên bàn cờ vua
Thực hành 1 trang 40 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho ba điểm D(−1;4),E(0;−3),F(5;0)...
Thực hành 2 trang 41 Toán 10 Tập 2: Cho hai vectơ →m=(−6;1),→n=(0;2)...
Thực hành 3 trang 42 Toán 10 Tập 2: Cho E(9;9),F(8;−7),G(0;−6). Tìm tọa độ các vectơ →FE,→FG,→EG...
Thực hành 4 trang 43 Toán 10 Tập 2: Cho tam giác QRS có tọa độ các đỉnh Q(7;−2),R(−4;9) và S(5;8)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.