Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 2. Đồ thị của hàm số y=ax^2 (a ≠ 0) trang 43,44,45,46,47,48 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 2. Đồ thị của hàm số y=ax^2 (a ≠ 0)
Phần câu hỏi bài 2 trang 43, 44 Vở bài tập toán 9 tập 2
Câu 5
Cho hàm số . Khoanh tròn vào chữ cái đặt trước câu đúng.
(A) Đồ thị của hàm số là một đường thẳng đi qua gốc tọa độ
(B) Đồ thị của hàm số là một đường thẳng nhận trục Oy làm trục đối xứng
(C) Đồ thị của hàm số là một đường cong nhận Oy làm trục đối xứng và đi qua gốc tọa độ.
(D) Nếu một đường cong nhận Oy làm trục đối xứng và đi qua gốc tọa độ thì đó là đồ thị hàm số
Phương pháp giải:
Sử dụng kiến thức về đồ thị hàm số
Trả lời:
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục làm trục đối xứng.
Chọn C.
Câu 6
Cho hàm số . Khoanh tròn vào chữ cái đặt trước câu đúng.
(A) Đồ thị của hàm số luôn luôn nằm phía trên trục Ox
(B) Mọi điểm của đồ thị hàm số đều không nằm trên trục hoành.
(C) Nếu a > 0 thì đồ thị hàm số nằm phía dưới trục hoành
(D) Với mọi có một điểm duy nhất của đồ thị hàm số thuộc trục hoành
Phương pháp giải:
Sử dụng kiến thức về đồ thị hàm số
Đồ thị của hàm số là một đường cong đi qua gốc tọa độ và nhận trục làm trục đối xứng. Đường cong đó là một parabol với đỉnh .
- Nếu thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
- Nếu thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Trả lời:
A sai vì đồ thị hàm số nằm dưới trục nếu
B sai vì đồ thị hàm số luôn đi qua gốc tọa độ thuộc trục hoành
C sai vì với thì đồ thị hàm số nằm trên trục hoành
D đúng vì đồ thị hàm số luôn đi qua gốc tọa độ thuộc trục hoành với mọi
Chọn D.
Câu 7
Cho hàm số . Các điểm (A(-2 ; -8); B(-1 ; -2); O(0 ; 0); B’(1 ; -2); A’(2 ; -8) thuộc đồ thị của hàm số. Khoanh tròn vào chữ cúa đặt trước cách vẽ đồ thị đúng.
(A) Nối A với A’, B với B’, B’ với O
(B) Nối A với B, B với O, O với A’, A’ với B’.
(C) Nối A với B, B với O, O với B’, B’ với A’.
(D) nối A với O, O với B, B với B’, B’ với A’.
Phương pháp giải:
Dựa vào cách vẽ đồ thị hàm số
Bước 1: Lập bảng giá trị đặc biệt tương ứng giữa và của hàm số .
Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số đi qua các điểm đặc biệt đó.
Nhận thấy rằng đồ thị hàm số có hình dạng là một đường cong parabol nên khi ta vẽ đồ thị hàm số thì nối các điểm ở mỗi phía của trục tung với nhau để tạo thành một đường cong trơn.
Trả lời:
Đồ thị hàm số
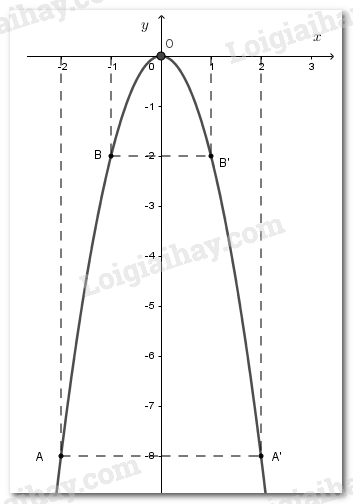
Ta nối các điểm A với B, B với O, O với , với để được đồ thị hàm số
Chọn B.
Câu 8
Khoanh tròn vào chữ cái đặt trước câu đúng.
(A) Hàm số có giá trị lớn nhất là 100
(B) Hàm số có giá trị lớn nhất là 0
(C) Hàm số không có giá trị nhỏ nhất
(D) Hàm số không có giá trị lớn nhất.
Phương pháp giải:
Ta sử dụng
+) Nếu thì với mọi ; khi . Giá trị nhỏ nhất của hàm số là .
+) Nếu thì với mọi ; khi . Giá trị lớn nhất của hàm số là .
Trả lời:
Hàm số có nên giá trị lớn nhất của nó là
Chọn B.
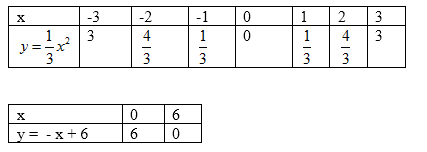
Cho hai hàm số . Điền vào những ô trống (…) ở các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ: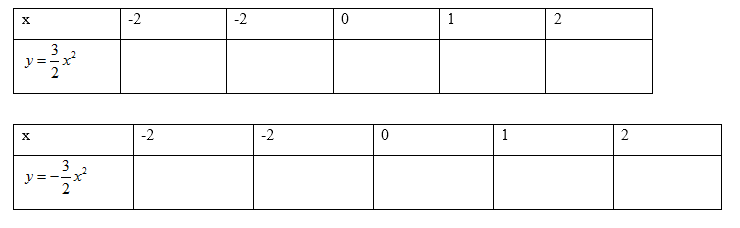
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Phương pháp giải:
Thay giá trị của vào hàm số cho trước để tính giá trị
Từ đó nhận xét về tính đối xứng của hai đồ thị
Trả lời:
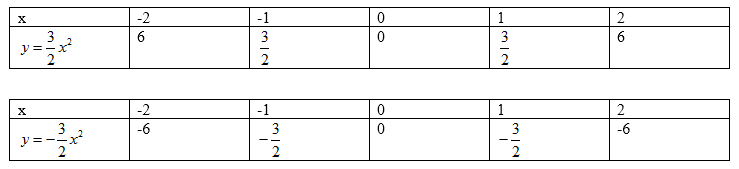
Vẽ đồ thị:
+) Vẽ đồ thị hàm số
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
+) Vẽ đồ thị hàm số
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
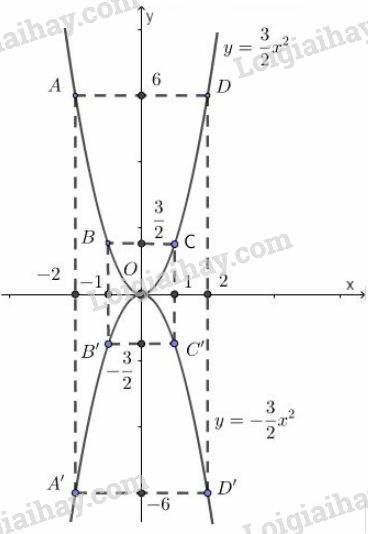
Hai đồ thị đối xứng nhau qua trục hoành.
Cho ba hàm số
LG a
Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ
Phương pháp giải:
Cách vẽ đồ thị hàm số
Bước 1: Lập bảng giá trị đặc biệt tương ứng giữa và của hàm số .
Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số đi qua các điểm đặc biệt đó.
Trả lời:
Ta có các bảng giá trị sau:
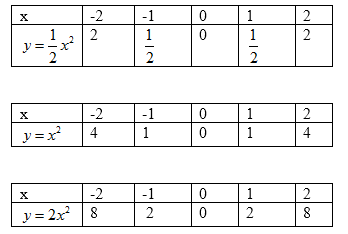
Đồ thị hàm số
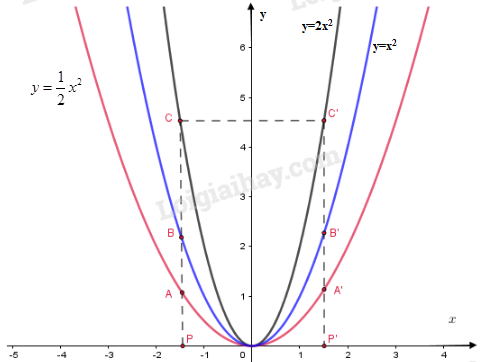
LG b
Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ của chúng.
Phương pháp giải:
Thay vào từng hàm số để tính
Trả lời:
Xác định điểm P trên trục Ox có hoành độ . Qua P kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị lần lượt tại
Thay vào các đẳng thức , lần lượt tính được:
Tung độ của điểm A là ;
Tung độ của điểm B là ;
Tung độ của điểm C là .
LG c
Tìm ba điểm A’, B', C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’, B và B’, C và C’.
Phương pháp giải:
Thay vào từng hàm số để tính
Trả lời:
Xác định điểm trên trục Ox có hoành độ . Qua kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị lần lượt tại
Thay vào các đẳng thức , lần lượt tính được:
Tung độ của điểm A’ là ;
Tung độ của điểm B’ là ;
Tung độ của điểm C’ là .
Hai điểm có hoành độ đối nhau và tung độ bằng nhau nên chúng đối xứng nhau qua trục Oy.
Tương tự, ta cũng có B và B’; C và C’ đối xứng nhau qua trục Oy.
LG d
Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số có giá trị nhỏ nhất.
Phương pháp giải:
Sử dụng: Nếu thì với mọi ; khi . Giá trị nhỏ nhất của hàm số là .
Trả lời:
Theo tính chất hàm số vì các hàm số đã cho đều có hệ số nên khi thì mỗi hàm số ấy đều có giá trị nhỏ nhất là
Trên mặt phẳng tọa độ, trên hình 13, có một điểm M thuộc đồ thị của hàm số y = ax2
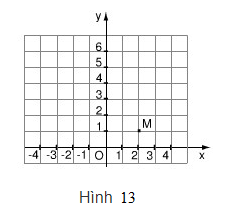
LG a
Tìm hệ số a
Phương pháp giải:
Thay tọa độ điểm M vào hàm số để tìm hệ số
Trả lời:
Theo hình 13, tọa độ của điểm là một điểm thuộc đồ thị Do đó, tọa độ của M phải thỏa mãn đẳng thức nghĩa là hay . Vậy
LG b
Điểm A(4 ; 4) có thuộc đồ thị không ?
Phương pháp giải:
Thay tọa độ điểm A vào hàm số tìm được để xác định xem A có thuộc đồ thị hay không?
Trả lời:
Thay vào đẳng thức , ta được . Điều này chứng tỏ tọa độ của điểm A thỏa mãn đẳng thức . Vậy điểm thuộc đồ thị hàm số
LG c
Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.
Phương pháp giải:
Tìm thêm điểm dựa vào tính đối xứng qua trục tung của đồ thị, từ đó vẽ đồ thị hàm số tìm được.
Trả lời:
Nhờ tính đối xứng của đồ thị qua Oy, không cần tính toán, có thể lấy thêm hai điểm lần lượt đối xứng với qua Oy. Hai điểm cũng thuộc đồ thị.
Từ đó ta vẽ đồ thị đi qua 5 điểm ta được đồ thị
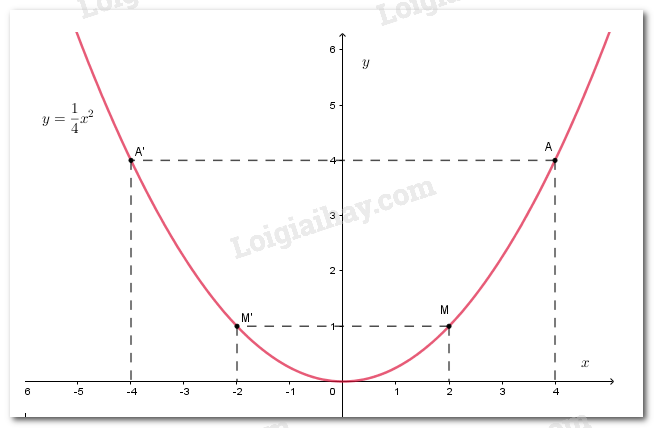
Biết rằng đường cong trên hình 14 là pararabol y = ax2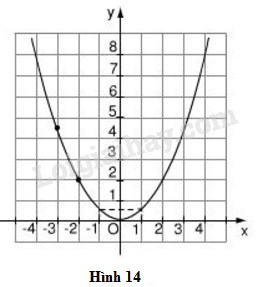
LG a
Tìm hệ số a
Phương pháp giải:
Thay tọa độ điểm xác định được trên hình vẽ vào hàm số để tìm hệ số
Trả lời:
Theo hình 14, điểm đã cho thuộc parabol có tọa độ là . Tọa độ của điểm này thỏa mãn đẳng thức . Do đó, ta có hay
Vậy
LG b
Tìm tung độ của điểm M thuộc parabol, biết rằng hoành độ của M là -3
Phương pháp giải:
Thay hoành độ của M vào hàm số tìm được để tìm tung độ
Trả lời:
Vì nên hàm số đã cho là . Điểm M thuộc đồ thị có hoành độ là thì tung độ của nó là
LG c
Tìm các điểm thuộc parabol có tung độ bằng 8
Phương pháp giải:
Thay tung độ vào hàm số tìm được để tìm hoành độ. Từ đó suy ra các điểm thỏa mãn.
Trả lời:
Giả sử điểm thuộc parabol. Khi đó tọa độ của A thỏa mãn đẳng thức Như vậy, . Do đó, , suy ra
Vậy các điểm cần tìm là .
Bài 8 trang 48 Vở bài tập toán 9 tập 2
Cho hai hàm số
LG a
Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
Phương pháp giải:
Cách vẽ đồ thị hàm số
Bước 1: Lập bảng giá trị đặc biệt tương ứng giữa và của hàm số .
Bước 2: Biểu diễn các điểm đặc biệt trên mặt phẳng tọa độ và vẽ đồ thị dạng parabol của hàm số đi qua các điểm đặc biệt đó.
Trả lời:
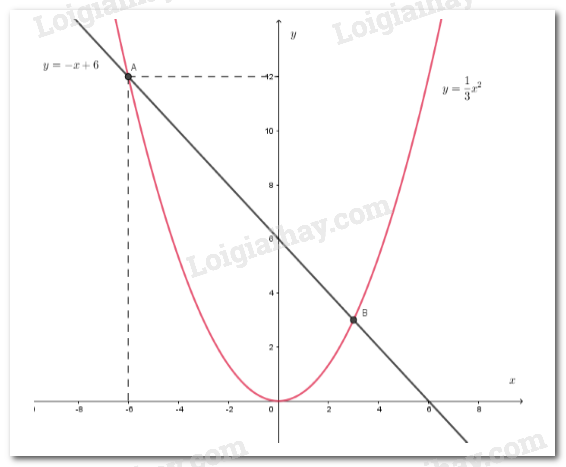
Vẽ đồ thị các hàm số (h. 15)
LG b
Tìm tọa độ các giao điểm của hai đồ thị đó.
Phương pháp giải:
Xác định giao điểm từ đồ thị hàm số đã vẽ.
Trả lời:
Hình 15 cho ta hai giao điểm
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.