Toán 9 (Cánh diều) Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Mai Hương Ngày: 08-03-2024 Lớp 9

Toptailieu biên soạn và giới thiệu lời giải Toán 9 (Cánh diều) Bài 1: Phương trình quy về phương trình bậc nhất một ẩn hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 9 Bài 1 từ đó học tốt môn Toán 9.

Toán 9 (Cánh diều) Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Khởi động trang 5 Toán 9 Tập 1: Trong một khu đất có dạng hình vuông, người ta dành một mảnh đất có dạng hình chữ nhật ở góc khu đất làm bể bơi. Biết diện tích của bể bơi bằng $1250 m^{2}$ . Độ dài cạnh của khu đất bằng bao nhiêu mét?

Lời giải:

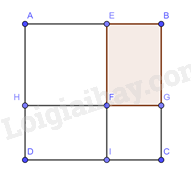
+ Ta có: AE = 50m, GC = 25m, AB là độ dài cạnh khu đất cần tìm.

+ Ta chia khu đất thành các hình:

- Hình vuông AEFH, FGCI.

- Hình chữ nhật EBGF, HFID.

+ Ta có: IC = FG = EB = GC.

Suy ra AB = AE + EB = 50 + 25 = 75 (m).

Suy ra Độ dài cạnh khu đất cần tìm là: 75m.

HĐ1

Hoạt động 1 trang 5 Toán 9 Tập 1:

a. Cho hai số thực $u, v$ có tích $u v = 0$ . Có nhận xét gì về giá trị của u, v?

b. Cho phương trình $(x - 3) (2 x + 1) = 0$ .

- Chứng tỏ rằng nghiệm của phương trình $x - 3 = 0$ và nghiêm của phương trình $2 x + 1 = 0$ đều là nghiệm của phương trình $(x - 3) (2 x + 1) = 0$ .

- Giả sử $x = x_{0}$ là nghiệm của phương trình $(x - 3) (2 x + 1) = 0$ . Giá trị $x = x_{0}^{}$ có phải là nghiệm của phương trình $x - 3 = 0$ hoặc phương trình $2 x + 1 = 0$ hay không?

Lời giải:

a. Nhận xét: u = 0 hoặc v = 0.

Ý 1:

+ Ta có: $x - 3 = 0 \Leftrightarrow x = 3$ .

+ Ta có: $2 x + 1 = 0 \Leftrightarrow x = - \frac{1}{2}$ .

Ý 2:

+ Thay $x = 3$ vào phương trình $(x - 3) (2 x + 1) = 0$ ta được:

$(3 - 3) (2.3 + 1) = 0 \Leftrightarrow 0.7 = 0 \Leftrightarrow 0 = 0$ (luôn đúng).

Vậy $x = 3$ là nghiệm của phương trình $(x - 3) (2 x + 1) = 0$ .

+ Thay $x = - \frac{1}{2}$ vào phương trình $(x - 3) (2 x + 1) = 0$ ta được:

$(- \frac{1}{2} - 3) [2. (- \frac{1}{2}) + 1] = 0 \Leftrightarrow - \frac{7}{2} .0 = 0 \Leftrightarrow 0 = 0$ (luôn đúng).

Vậy $x = - \frac{1}{2}$ là nghiệm của phương trình $(x - 3) (2 x + 1) = 0$ .

Ý 3:

Khi $x = x_{0}^{}$ là nghiệm của phương trình $(x - 3) (2 x + 1) = 0$ thì $x = x_{0}^{}$ có là nghiệm của phương trình $x - 3 = 0$ hoặc phương trình $2 x + 1 = 0$ .

LT1

Luyện tập 1 trang 6 Toán 9 Tập 1: Giải phương trình: $(4 x + 5) (3 x - 2) = 0$ .

Lời giải:

Để giải phương trình trên ta giải hai phương trình sau:

*) $4 x + 5 = 0$

$x = - \frac{5}{4}$ ;

*) $3 x - 2 = 0$

$x = \frac{2}{3}$ .

Vậy phương trình đã cho có hai nghiệm là $x = - \frac{5}{4}$ và $x = \frac{2}{3}$ .

LT2

Luyện tập 2 trang 7 Toán 9 Tập 1: Giải các phương trình:

a. $x^{2} - 10 x + 25 = 5 (x - 5)$ ;

b. $4 x^{2} - 16 = 5 (x + 2)$ .

Lời giải:

a. $x^{2} - 10 x + 25 = 5 (x - 5)$

Ta có: $x^{2} - 10 x + 25 = 5 (x - 5)$

$\begin{array}{l} {(x - 5)}^{2} = 5 (x - 5) \\ {(x - 5)}^{2} - 5 (x - 5) = 0 \\ (x - 5) (x - 5 - 5) = 0 \end{array}$

$(x - 5) (x - 10) = 0.$

Để giải phương trình trên, ta giải hai phương trình sau:

*) $x - 5 = 0$

$x = 5;$

*) $x - 10 = 0$

$x = 10.$

Vậy phương trình đã cho có hai nghiệm là $x = 5$ và $x = 10$ .

HĐ2

Hoạt động 2 trang 7 Toán 9 Tập 1: Cho phương trình: $\frac{x + 2}{x} = \frac{x - 3}{x - 2} (1)$ .

Tìm điều kiện của $x$ để cả hai mẫu thức có trong phương trình (1) là khác 0.

Cho mẫu của cả hai phân thức rồi giải điều kiện.

Lời giải:

Để mẫu thức trong phương trình (1) khác 0.

${\begin{cases} x \neq 0 \\ x - 2 \neq 0 \end{cases}$ hay ${\begin{cases} x \neq 0 \\ x \neq 2 \end{cases}$

Vậy $x \neq 0; x \neq 2$ thì mẫu thức trong phương trình (1) khác 0.

LT3

Luyện tập 3 trang 7 Toán 9 Tập 1: Tìm điều kiện xác định của phương trình $\frac{x - 8}{x - 7} = 8 + \frac{1}{1 - x}$ .

Lời giải:

Điều kiện xác định của phương trình $\frac{x - 8}{x - 7} = 8 + \frac{1}{1 - x}$ là $x - 7 \neq 0$ và $1 - x \neq 0$ hay $x \neq 7$ và $x \neq 1$ .

HĐ3

Hoạt động 3 trang 8 Toán 9 Tập 1: Cho phương trình: $\frac{2 x + 1}{2 x} = 1 - \frac{2}{x - 3} (2)$

Hãy giả phương trình (2) theo các bước sau:

a. Tìm điều kiện xác định của phương trình (2).

b. Tìm mẫu thức chung, quy đồng mẫu thức các phân thức ở hai vế của phương trình (2) và khử mẫu.

c. Giải phương trình vừa tìm được.

d. Kiểm tra điều kiện xác định của phương trình (2) đối với các giá trị của ẩn vừa tìm được rồi kết luận.

Lời giải:

a. Điều kiện xác định của phương trình $\frac{2 x + 1}{2 x} = 1 - \frac{2}{x - 3}$ là $2 x \neq 0$ và $x - 3 \neq 0$ hay $x \neq 0$ và $x \neq 3$ .

+ Mẫu thức chung của phương trình là: $2 x (x - 3)$ .

+ Quy đồng mẫu thức: $\frac{(2 x + 1) (x - 3)}{2 x (x - 3)} = \frac{2 x (x - 3)}{2 x (x - 3)} - \frac{4 x}{2 x (x - 3)}$ .

+ Khử mẫu: $(2 x + 1) (x - 3) = 2 x (x - 3) - 4 x$ .

c. Giải phương trình: $(2 x + 1) (x - 3) = 2 x (x - 3) - 4 x$ .

$\begin{array}{l} 2 x^{2} - 6 x + x - 3 = 2 x^{2} - 6 x - 4 x \\ 2 x^{2} - 6 x + x - 3 - 2 x^{2} + 6 x + 4 x = 0 \\ 5 x - 3 = 0 \end{array}$

$x = \frac{3}{5}$ .

d. Ta thấy $x = \frac{3}{5}$ thỏa mãn điều kiện xác định của phương trình.

LT4

Luyện tập 4 trang 9 Toán 9 Tập 1: Giải phương trình: $\frac{x}{x - 2} + \frac{1}{x - 3} = \frac{2}{(2 - x) (x - 3)}$ .

Lời giải:

Điều kiện xác định: $x \neq 2$ và $x \neq 3$

$\frac{x}{x - 2} + \frac{1}{x - 3} = \frac{2}{(2 - x) (x - 3)}$

$\begin{array}{l} \frac{x (x - 3)}{(x - 2) (x - 3)} + \frac{x - 2}{(x - 2) (x - 3)} = - \frac{2}{(x - 2) (x - 3)} \\ \frac{x^{2} - 3 x}{(x - 2) (x - 3)} + \frac{x - 2}{(x - 2) (x - 3)} = - \frac{2}{(x - 2) (x - 3)} \\ x^{2} - 3 x + x - 2 = - 2 \\ x^{2} - 2 x - 2 + 2 = 0 \\ x^{2} - 2 x = 0 \end{array}$

$x (x - 2) = 0$ .

Để giải phương trình trên, ta giải hai phương trình:

*) $x = 0$ . *) $x - 2 = 0$

$x = 2$ .

Ta thấy:

+ $x = 0$ thỏa mãn điều kiện xác định của phương trình;

+ $x = 2$ không thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm $x = 0$ .

LT5

Luyện tập 5 trang 10 Toán 9 Tập 1: Một đội công nhân làm đường nhận nhiệm vụ trải nhựa $8100 m^{2}$ mặt đường. Ở giai đoan đầu, đội trải được $3600 m^{2}$ mặt đường. Ở giai đoạn hai đội công nhân tăng năng suất thêm $300 m^{2} /$ ngày rồi hoàn thành công việc. Hỏi đội công nhân đã hoàn thành công việc trong bao nhiêu ngày? Biết rằng năng suất lao động của đội không thay đổi ở mỗi giai đoạn và thời gian làm việc của hai giai đoạn là như nhau.

Lời giải:

Gọi số ngày đội công nhân hoàn thành công việc là: x (ngày, x > 0).

Thời gian làm việc của đội ở mỗi giai đoạn là: $\frac{x}{2}$ (ngày).

Năng suất lao động của đội ở giai đoạn 1 là: $3600 : \frac{x}{2} = 7200 x$ ( $m^{2}$ /ngày).

Giai đoạn 2 đội trải được: $8100 - 3600 = 4500 (m^{2})$

Năng suất lao động của đội ở giai đoạn 2 là: $4500 : \frac{x}{2} = 9000 x$ ( $m^{2}$ /ngày).

Do giai đoạn hai, đội công nhân tăng năng suất thêm $300$ ( $m^{2}$ /ngày). Ta có phương trình:

$9000 x - 7200 x = 300$ .

Giải phương trình: $9000 x - 7200 x = 300$

$1800 x = 300$

$x = \frac{1}{6}$ (thỏa mãn điều kiện x > 0).

Vậy đội công nhân hoàn thành công việc trong $\frac{1}{6}$ ngày.

Bài 1 trang 11 Toán 9 Tập 1: Giải các phương trình:

a. $(9 x - 4) (2 x + 5) = 0$ ;

b. $(1, 3 x + 0, 26) (0, 2 x - 4) = 0$ ;

c. $2 x (x + 3) - 5 (x + 3) = 0$ ;

d. $x^{2} - 4 + (x + 2) (2 x - 1) = 0$ .

Lời giải:

a. $(9 x - 4) (2 x + 5) = 0$

Để giải phương trình đã cho, ta giải hai phương trình sau:

*) $9 x - 4 = 0$

$x = \frac{4}{9}$ ;

*) $2 x + 5 = 0$

$x = - \frac{5}{2}$ .

Vậy phương trình có nghiệm $x = \frac{4}{9}$ và $x = - \frac{5}{2}$ .

b. $(1, 3 x + 0, 26) (0, 2 x - 4) = 0$

Để giải phương trình đã cho, ta giải hai phương trình sau:

*) $1, 3 x + 0, 26 = 0$

$x = 0, 2$ ;

*) $0, 2 x - 4 = 0$

$x = 20$ .

Vậy phương trình có nghiệm $x = 0, 2$ và $x = 20$ .

c. $2 x (x + 3) - 5 (x + 3) = 0$

$(2 x - 5) (x + 3) = 0$ .

Để giải phương trình đã cho, ta giải hai phương trình sau:

*) $2 x - 5 = 0$

$x = \frac{5}{2}$ ;

*) $x + 3 = 0$

$x = - 3$ .

Vậy phương trình có nghiệm $x = \frac{5}{2}$ và $x = - 3$ .

d. $x^{2} - 4 + (x + 2) (2 x - 1) = 0$

$(x - 2) (x + 2) + (x + 2) (2 x - 1) = 0$

$(x + 2) (x - 2 + 2 x - 1) = 0$

$(x + 2) (3 x - 3) = 0$

Để giải phương trình đã cho, ta giải hai phương trình sau:

*) $x + 2 = 0$

$x = - 2$ ;

*) $3 x - 3 = 0$

$x = 1$ .

Vậy phương trình đã cho có nghiệm $x = - 2$ và $x = 1$ .

Bài 2 trang 11 Toán 9 Tập 1: Giải các phương trình:

a. $\frac{1}{x} = \frac{5}{3 (x + 2)}$ ;

b. $\frac{x}{2 x - 1} = \frac{x - 2}{2 x + 5}$ ;

c. $\frac{5 x}{x - 2} = 7 + \frac{10}{x - 2}$ ;

d. $\frac{x^{2} - 6}{x} = x + \frac{3}{2}$ .

Lời giải:

a. $\frac{1}{x} = \frac{5}{3 (x + 2)}$

Điều kiện xác định: $x \neq 0$ và $x \neq - 2$ .

$\frac{1}{x} = \frac{5}{3 (x + 2)}$

$\begin{array}{l} \frac{3 (x + 2)}{3 x (x + 2)} = \frac{5}{3 x (x + 2)} \\ 3 (x + 2) = 5 \\ 3 x + 6 - 5 = 0 \\ 3 x + 1 = 0 \end{array}$

$x = \frac{- 1}{3}$ .

Ta thấy $x = - \frac{1}{3}$ thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm $x = - \frac{1}{3}$ .

b. $\frac{x}{2 x - 1} = \frac{x - 2}{2 x + 5}$

Điều kiện xác định: $x \neq \frac{1}{2}$ và $x \neq - \frac{5}{2}$ .

$\frac{x}{2 x - 1} = \frac{x - 2}{2 x + 5}$

$\begin{array}{l} \frac{x (2 x + 5)}{(2 x - 1) (2 x + 5)} = \frac{(x - 2) (2 x - 1)}{(2 x - 1) (2 x + 5)} \\ x (2 x + 5) = (x - 2) (2 x - 1) \\ 2 x^{2} + 5 x = 2 x^{2} - x - 4 x + 2 \\ 2 x^{2} + 5 x - 2 x^{2} + x + 4 x - 2 = 0 \\ 10 x - 2 = 0 \end{array}$

$x = \frac{1}{5}$ .

Ta thấy $x = \frac{1}{5}$ thỏa mãn điều kiện xác định của phương trình.

Vậy $x = \frac{1}{5}$ là nghiệm của phương trình đã cho.

c. $\frac{5 x}{x - 2} = 7 + \frac{10}{x - 2}$

Điều kiện xác định: $x \neq 2$ .

$\frac{5 x}{x - 2} = 7 + \frac{10}{x - 2}$

$\begin{array}{l} \frac{5 x}{x - 2} = \frac{7 (x - 2)}{x - 2} + \frac{10}{x - 2} \\ 5 x = 7 x - 14 + 10 \\ 5 x - 7 x + 14 - 10 = 0 \\ 2 x + 4 = 0 \end{array}$

$x = - 2$ .

Ta thấy $x = - 2$ thỏa mãn điều kiện xác định của phương trình.

Vậy $x = - 2$ là nghiệm của phương trình đã cho.

d. $\frac{x^{2} - 6}{x} = x + \frac{3}{2}$

Điều kiện xác định: $x \neq 0$ .

$\frac{x^{2} - 6}{x} = x + \frac{3}{2}$

$\begin{array}{l} \frac{2 (x^{2} - 6)}{2 x} = \frac{2 x^{2}}{2 x} + \frac{3 x}{2 x} \\ 2 (x^{2} - 6) = 2 x^{2} + 3 x \\ 2 x^{2} - 12 = 2 x^{2} + 3 x \\ 2 x^{2} - 12 - 2 x^{2} - 3 x = 0 \\ - 3 x - 12 = 0 \end{array}$

$x = - 4$ .

Ta thấy $x = - 4$ thỏa mãn điều kiện xác định của phương trình.

Vậy $x = - 4$ là nghiệm của phương trình đã cho.

Bài 3 trang 11 Toán 9 Tập 1: Một ca nô đi xuôi dòng từ địa điểm A đến địa điểm B, rồi lại đi ngược dòng từ địa điểm B trở về địa điểm A. Thời gian cả đi và về là 3 giờ. Tính tốc độ của dòng nước. Biết tốc độ của ca nô khi nước yên lặng là 27km/h và độ dài quãng đường AB là 40km.

Lời giải:

Gọi tốc độ của dòng nước là: $x$ (km/h, 0 < x < 27)

Vận tốc cano khi xuôi dòng là: $27 + x$ (km/h);

Vận tốc cano khi ngược dòng là: $27 - x$ (km/h);

Thời gian cano khi xuôi dòng là: $\frac{40}{27 + x}$ (giờ);

Thời gian cano khi ngược dòng là: $\frac{40}{27 - x}$ (giờ).

Do thời gian cả đi và về là 3 giờ nên ta có phương trình:

$\frac{40}{27 + x} + \frac{40}{27 - x} = 3$

$\frac{40 (27 - x)}{(27 + x) (27 - x)} + \frac{40 (27 + x)}{(27 + x) (27 - x)} = \frac{3 (27 + x) (27 - x)}{(27 + x) (27 - x)}$

$1080 - 40 x + 1080 + 40 x = 3 (729 - x^{2})$

$2160 = 2187 - 3 x^{2}$

$3 x^{2} - 27 = 0$

$3 x^{2} = 27$

$x^{2} = 9$

$x = 3$ (Thỏa mãn điều kiện).

Vậy tốc độ của dòng nước là 3 (km/h).

Bài 4 trang 11 Toán 9 Tập 1: Một doanh nghiệp sử dụng than để sản xuất sản phẩm. Doanh nghiệp đó lập kế hoạch tài chính cho việc loại bỏ chất ô nhiễm khí thải theo dự kiến sau: Để loại bỏ chất ô nhiễm trong khí thải thì chi phí (Triệu đồng) được tính theo công thức: với . Với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được bao nhiêu phần trăm chất gây ô nhiễm trong khí thải (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Với chi phí là 420 triệu đồng ta có: $420 = \frac{80}{100 - p}$

$4200 - 420 p = 80$

$420 p = 4120$

$p \approx 9, 8$ .

Vậy với chi phí là 420 triệu đồng thì doanh nghiệp loại bỏ được 9,8% chất gây ô nhiễm trong khí thải.

Bài 5 trang 11 Toán 9 Tập 1: Bạn Hoa dự định dùng hết số tiền 600 nghìn đồng để mua một số chiếc áo đồng giá tặng các bạn có hoàn cảnh khó khăn. Khi đến cửa hàng, loại áo mà bạn Hoa dự định mua được giảm giá 30 nghìn đồng/chiếc. Do vậy, bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định. Tính giá tiền của mỗi chiếc áo bạn Hoa đã mua.

Lời giải:

Gọi giá tiền của mỗi chiếc áo bạn Hoa đã mua là $x$ (nghìn đồng, $0 < x < 600$ ).

Giá tiền của mỗi chiếc áo bạn Hoa dự định mua là: $x - 30$ (nghìn đồng)

Số lượng áo bạn Hoa đã mua là: $\frac{600}{x}$ (chiếc)

Số lượng áo bạn Hoa dự định mua là: $\frac{600}{x - 30}$ (chiếc)

Do bạn Hoa đã mua được số lượng áo gấp 1,25 lần so với số lượng dự định nên ta có phương trình:

$1, 25. \frac{600}{x} = \frac{600}{x - 30}$

$\frac{750 (x - 30)}{x (x - 30)} = \frac{600 x}{x (x - 30)}$

$750 x - 22500 = 600 x$

$750 x - 600 x = 22500$

$150 x = 22500$

$x = 150$ (Thoả mãn điều kiện).

Vậy giá tiền mỗi chiếc áo bạn Hoa đã mua là 150 nghìn đồng.

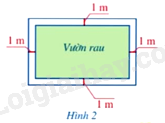
Bài 6 trang 11 Toán 9 Tập 1: Trên một mảnh đất có dạng hình chữ nhật với chu vi bằng 52m. Trên mảnh đất đó, người ta làm một vườn có dạng hình chữ nhật có diện tích là $112 m^{2}$ và một lối đi xung quanh vườn rộng 1m (Hình 2). Tính các kích thước của mảnh đất đó.

Lời giải:

Nửa chu vi của mảnh đất là: $52 : 2 = 26 (m)$

Gọi chiều dài của mảnh đất là $x (m, 2 < x < 26)$ .

Chiều rộng của mảnh đất là: $26 - x (m)$

Chiều dài của vườn rau là: $x - 2 (m)$

Chiều rộng của vườn rau là: $26 - x - 2 = 24 - x (m)$

Do diện tích của vườn rau là $112 m^{2}$ nên ta có phương trình:

$(x - 2) (24 - x) = 112$

$24 x - x^{2} - 48 + 2 x - 112 = 0$

$- x^{2} + 26 x - 160 = 0$

$x^{2} - 26 x + 160 = 0$

${(x - 13)}^{2} - 9 = 0$

$(x - 13 - 3) (x - 13 + 3) = 0$

$(x - 16) (x - 10) = 0$ .

Để giải phương trình trên, ta giải hai phương trình sau:

*) $x - 16 = 0$

$x = 16$ ;

*) $x - 10 = 0$

$x = 10$ .

Vậy chiều dài của mảnh đất là $16 (m)$

Chiều rộng của mảnh đất là $10 (m)$

Xem thêm các bài giải SGK Toán lớp 9 Cánh diều hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 9

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương