Toán 12 (Kết nối tri thức) Bài 6: Vectơ trong không gian

Mai Hương Ngày: 15-03-2024 Lớp 12

173

Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Kết nối tri thức) Bài 6: Vectơ trong không gian hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 6 từ đó học tốt môn Toán 12.

Toán 12 (Kết nối tri thức) Bài 6: Vectơ trong không gian

Hoạt động 1 trang 46 SGK Toán 12 Tập 1: Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các các lực căng dây?

b) Các đoạn thẳng này có cùng nằm trong một mặt phẳng không?

Lời giải:

a) Các đoạn thẳng này có hướng lên trên (về phía móc cần cẩu) và độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.

b) Các đoạn thẳng này không cùng nằm trên một mặt phẳng.

Câu hỏi trang 46 SGK Toán 12 Tập 1: Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Lời giải:

Một số ví dụ khác:

a) Hướng bay của khinh khí cầu:

b) Hướng đi của thuyền trên sông:

Luyện tập 1 trang 47 SGK Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ $\vec{A C}, \vec{A D}, \vec{A D^{'}}$ :

a) Hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD)?

b) Hai vectơ nào có cùng độ dài?

Lời giải:

a) Trong các vectơ $\vec{A C}, \vec{A D}, \vec{A D^{'}}$ , hai vectơ $\vec{A C}, \vec{A D}$ có giá nằm trong mặt phẳng (ABCD)

b) Vì ABCD.A’B’C’D’ là hình lập phương nên $A D = D C = D D^{'}$

Tam giác ADD’ vuông tại D nên theo định lý Pythagore ta có:

$A D^{'} = \sqrt{A D^{2} + D D^{' 2}} = A D \sqrt{2}$

Tam giác ADC vuông tại D nên theo định lý Pythagore ta có:

$A C = \sqrt{A D^{2} + D C^{2}} = A D \sqrt{2}$

Do đó, $A D^{'} = A C$ hay $| \vec{A C} | = | \vec{A D^{'}} |$ . Vậy hai vectơ $\vec{A C}, \vec{A D^{'}}$ có cùng độ dài.

Hoạt động 2 trang 47 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.7)

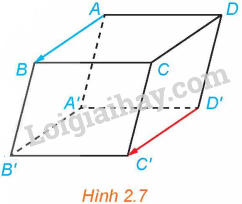
a) So sánh độ dài hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ .

b) Nhận xét về giá của hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ .

c) Hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ có cùng phương không? Có cùng hướng không?

Lời giải:

a) Vì ABCD.A’B’C’D’ là hình hộp nên ABCD và DCC’D’ là các hình bình hành. Suy ra, $A B = C D = D^{'} C^{'}$ . Do đó, $| \vec{A B} | = | \vec{D^{'} C^{'}} |$ .

b) Vì ABCD và DCC’D’ là các hình bình hành nên AB//CD, CD//C’D’. Do đó, AB//C’D’. Vậy giá của hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ song song với nhau.

c) Hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ cùng phương và cùng hướng.

Câu hỏi trang 47 SGK Toán 12 Tập 1: Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?

Lời giải:

Giả sử có ba vectơ $\vec{a}$ , $\vec{b}$ và $\vec{c}$ sao cho: $\vec{a} = \vec{b}$ và $\vec{b} = \vec{c}$ .

Vì $\vec{a} = \vec{b}$ nên hai vectơ $\vec{a}$ , $\vec{b}$ có cùng hướng và $| \vec{a} | = | \vec{b} |$ (1)

Vì $\vec{b} = \vec{c}$ nên hai vectơ $\vec{c}$ , $\vec{b}$ có cùng hướng và $| \vec{c} | = | \vec{b} |$ (2)

Từ (1) và (2) ta có hai vectơ $\vec{a}$ , $\vec{c}$ có cùng hướng và $| \vec{a} | = | \vec{c} |$ . Do đó, $\vec{a} = \vec{c}$

Do đó, hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó bằng nhau.

Luyện tập 2 trang 48 SGK Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.

a) Trong ba vectơ $\vec{S C}, \vec{A D}$ và $\vec{D C}$ , vectơ nào bằng vectơ $\vec{A B}$ .

b) Gọi M là một điểm thuộc cạnh AD. Xác định điểm N sao cho $\vec{M N} = \vec{A B}$ .

Lời giải:

a) Vì ABCD là hình bình hành nên AB//CD và $A B = C D$ . Do đó, hai vectơ $\vec{A B}$ và $\vec{D C}$ có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.

Vì AB và SC chéo nhau nên hai vectơ $\vec{A B}$ và $\vec{S C}$ không cùng phương. Do đó, hai vectơ $\vec{A B}$ và $\vec{S C}$ không bằng nhau.

Vì hai vectơ $\vec{A B}$ và $\vec{A D}$ không cùng phương nên hai vectơ $\vec{A B}$ và $\vec{A D}$ không bằng nhau.

b) Qua M vẽ đường thẳng song song với AB cắt BC tại N.

Tứ giác ABNM có: AB//MN, AM//BN nên tứ giác ABNM là hình bình hành. Do đó, $A B = M N$ , lại có: AB//MN nên hai vectơ $\vec{M N}, \vec{A B}$ cùng độ dài và cùng hướng. Suy ra, $\vec{M N} = \vec{A B}$ . Vậy điểm N cần tìm là giao điểm của đường thẳng qua M song song với AB và cạnh BC.

Vận dụng 1 trang 48 SGK Toán 12 Tập 1: Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.

Lời giải:

Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là $\vec{a}$ . Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 22 lên tầng 29 của tòa nhà là $\vec{b}$ .

Vì hai vectơ $\vec{a}$ và $\vec{b}$ đều dịch chuyển từ tầng thấp lên tầng cao nên hai vectơ $\vec{a}$ và $\vec{b}$ có cùng hướng (1).

Độ dài vectơ $\vec{a}$ là: $| \vec{a} | = 7$ , độ dài vectơ $\vec{b}$ là: $| \vec{b} | = 7$ nên $| \vec{a} | = | \vec{b} | = 7$ (2)

Từ (1) và (2) ta có: $\vec{a} = \vec{b}$ . Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.

Hoạt động 3 trang 49 SGK Toán 12 Tập 1:Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Lấy điểm A và vẽ các vectơ $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Lấy điểm A’ và vẽ các vectơ $\vec{A^{'} B^{'}} = \vec{a}, \vec{B^{'} C^{'}} = \vec{b}$ (H.2.10).

a) Giải thích vì sao $\vec{A A^{'}} = \vec{B B^{'}}$ và $\vec{B B^{'}} = \vec{C C^{'}}$ .

b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra $\vec{A C} = \vec{A^{'} C^{'}}$ .

Lời giải:

a) Vì $\vec{A B} = \vec{a}$ nên hai vectơ $\vec{a}$ và $\vec{A B}$ cùng hướng và cùng độ dài.

Vì $\vec{A^{'} B^{'}} = \vec{a}$ nên hai vectơ $\vec{a}$ và $\vec{A^{'} B^{'}}$ cùng hướng và cùng độ dài.

Do đó, hai vectơ $\vec{A^{'} B^{'}}$ và $\vec{A B}$ cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và $A B = A^{'} B^{'}$ . Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và $A A^{'} = B B^{'} \Rightarrow$ hai vectơ $\vec{A A^{'}}, \vec{B B^{'}}$ có cùng hướng và cùng độ dài. Suy ra, $\vec{A A^{'}} = \vec{B B^{'}}$ .

Vì $\vec{B C} = \vec{b}$ nên hai vectơ $\vec{b}$ và $\vec{B C}$ cùng hướng và cùng độ dài.

Vì $\vec{B^{'} C^{'}} = \vec{b}$ nên hai vectơ $\vec{b}$ và $\vec{B^{'} C^{'}}$ cùng hướng và cùng độ dài.

Do đó, hai vectơ $\vec{B C}$ và $\vec{B^{'} C^{'}}$ cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và $B C = B^{'} C^{'}$ . Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và $C C^{'} = B B^{'} \Rightarrow$ hai vectơ $\vec{B B^{'}}, \vec{C C^{'}}$ có cùng hướng và cùng độ dài. Suy ra, $\vec{B B^{'}} = \vec{C C^{'}}$ .

b) Vì hai vectơ $\vec{A A^{'}}, \vec{B B^{'}}$ có cùng hướng và cùng độ dài; hai vectơ $\vec{B B^{'}}, \vec{C C^{'}}$ có cùng hướng và cùng độ dài nên hai vectơ $\vec{A A^{'}}$ và $\vec{C C^{'}}$ có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và $A A^{'} = C C^{'}$ nên tứ giác AA’C’C là hình bình hành. Suy ra, $A C = A^{'} C^{'}$ và AC//A’C’. Do đó, hai vectơ $\vec{A C}, \vec{A^{'} C^{'}}$ có cùng hướng và cùng độ dài. Suy ra, $\vec{A C} = \vec{A^{'} C^{'}}$ .

Luyện tập 3 trang 50 SGK Toán 12 Tập 1: Trong Ví dụ 3, hãy tính độ dài của vectơ $\vec{A C} + \vec{C^{'} D^{'}}$ .

Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).

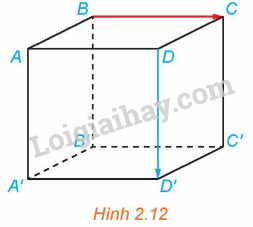
Lời giải:

Vì ABCD.A’B’C’D’ là hình lập phương nên DCC’D’ là hình vuông. Do đó, $\vec{C^{'} D^{'}} = \vec{C D}$ .

Ta có: $\vec{A C} + \vec{C^{'} D^{'}} = \vec{A C} + \vec{C D} = \vec{A D}$

Vì độ dài mỗi cạnh hình lập phương ABCD.A’B’C’D’ bằng 1 nên $| \vec{A D} | = 1$ .

Vậy $| \vec{A C} + \vec{C^{'} D^{'}} | = 1$

Luyện tập 4 trang 50 SGK Toán 12 Tập 1: Cho tứ diện ABCD (H.2.13). Chứng minh rằng $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$ .

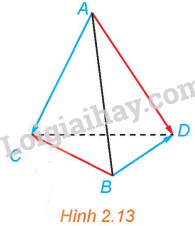
Lời giải:

Ta có: $\vec{A B} + \vec{C D} = \vec{A D} + \vec{D B} + \vec{C B} + \vec{B D} = (\vec{A D} + \vec{C B}) + (\vec{D B} + \vec{B D})$

$= \vec{A D} + \vec{C B} + \vec{D D} = \vec{A D} + \vec{C B}$ (đpcm)

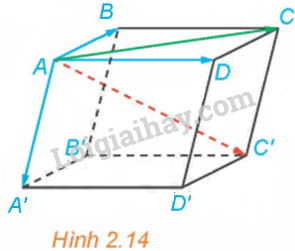
Hoạt động 4 trang 50 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.14).

a) Hai vectơ $\vec{A B} + \vec{A D}$ và $\vec{A C}$ có bằng nhau hay không?

b) Hai vectơ $\vec{A B} + \vec{A D} + \vec{A A^{'}}$ và $\vec{A C^{'}}$ có bằng nhau hay không?

Lời giải:

a) Vì ABCD là hình bình hành nên $\vec{A B} + \vec{A D} = \vec{A C}$

b) Ta có: $\vec{A B} + \vec{A D} + \vec{A A^{'}} = \vec{A C} + \vec{A A^{'}}$ (1)

Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, $A A^{'} = D D^{'}$ và $D D^{'} = C C^{'}$ , DD’//CC’. Suy ra, AA’//CC’ và $A A^{'} = C C^{'}$ . Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: $\vec{A C} + \vec{A A^{'}} = \vec{A C^{'}}$ (2)

Từ (1) và (2) ta có: $\vec{A B} + \vec{A D} + \vec{A A^{'}} = \vec{A C^{'}}$

Câu hỏi trang 50 SGK Toán 12 Tập 1: Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.

Lời giải:

Quy tắc hình hộp với các vectơ có điểm đầu là B là: $\vec{B A} + \vec{B C} + \vec{B B^{'}} = \vec{B D^{'}}$

Luyện tập 5 trang 50 SGK Toán 12 Tập 1: Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng $\vec{B B^{'}} + \vec{C D} + \vec{A D} = \vec{B D^{'}}$

Lời giải:

Vì ABCD là hình chữ nhật nên $\vec{A D} = \vec{B C}, \vec{C D} = \vec{B A}$

Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên $\vec{B B^{'}} + \vec{B A} + \vec{B C} = \vec{B D^{'}}$

Ta có: $\vec{B B^{'}} + \vec{C D} + \vec{A D} = \vec{B B^{'}} + \vec{B A} + \vec{B C} = \vec{B D^{'}}$

Hoạt động 5 trang 51 SGK Toán 12 Tập 1: Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.

Lời giải:

Các vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.

Luyện tập 6 trang 52 SGK Toán 12 Tập 1: Trong Ví dụ 6, chứng minh rằng:

a) $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau;

b) $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S C}$

Lời giải:

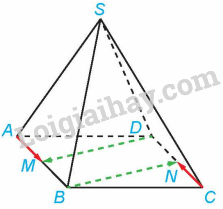
a) Tứ giác ABCD là hình bình hành nên $A B = C D$ , AB//CD. Suy ra $B M = D N$ (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, $B N = D M$ và BN//DM. Hai vectơ $\vec{B N}$ và $\vec{D M}$ có cùng độ dài và ngược hướng nên $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau.

b) Theo a ta có: $\vec{B N} = - \vec{D M}$

Do đó, $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S D} + \vec{D M} + \vec{M C} = \vec{S M} + \vec{M C} = \vec{S C}$

Vận dụng 2 trang 52 SGK Toán 12 Tập 1: Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.

Lời giải:

Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.

Hoạt động 6 trang 52 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)

a) Hai vectơ $\vec{M N}$ và $\vec{B^{'} C^{'}}$ có cùng phương không? Có cùng hướng không?

b) Giải thích vì sao $| \vec{M N} | = \frac{1}{2} | \vec{B^{'} C^{'}} |$ .

Lời giải:

a) Vì MN là đường trung bình của tam giác ABC nên MN//BC.

Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.

Do đó hai vectơ $\vec{M N}$ và $\vec{B^{'} C^{'}}$ có cùng phương và cùng hướng.

b) Vì BCC’B’ là hình bình hành nên $B C = B^{'} C^{'}$

Vì MN là đường trung bình của tam giác ABC nên $M N = \frac{1}{2} B C$

Suy ra: $| \vec{M N} | = \frac{1}{2} | \vec{B^{'} C^{'}} |$ .

Câu hỏi trang 53 SGK Toán 12 Tập 1: Hai vectơ $1 \vec{a}$ và $\vec{a}$ có bằng nhau không? Hai vectơ $(- 1) \vec{a}$ và $- \vec{a}$ có bằng nhau không?

Lời giải:

Hai vectơ $1 \vec{a}$ và $\vec{a}$ bằng nhau vì chúng có cùng độ dài và cùng hướng.

Hai vectơ $(- 1) \vec{a}$ và $- \vec{a}$ bằng nhau chúng có cùng độ dài và cùng hướng.

Luyện tập 7 trang 53 SGK Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho $S E = \frac{1}{3} S A, S F = \frac{1}{3} S B$ . Chứng minh rằng $\vec{E F} = \frac{1}{3} \vec{D C}$ .

Lời giải:

Vì $S E = \frac{1}{3} S A, S F = \frac{1}{3} S B \Rightarrow \frac{S E}{S A} = \frac{S F}{S B} (= \frac{1}{3})$

Tam giác SAB có: $\frac{S E}{S A} = \frac{S F}{S B}$ nên FE//AB và $E F = \frac{1}{3} A B$ .

Vì hai vectơ $\vec{E F}$ và $\vec{A B}$ cùng hướng nên $\vec{E F} = \frac{1}{3} \vec{A B}$ (1)

Vì ABCD là hình bình hành nên $A B = C D$ và AB//CD. Do đó, $\vec{A B} = \vec{D C}$ (2)

Từ (1) và (2) ta có: $\vec{E F} = \frac{1}{3} \vec{D C}$

Luyện tập 8 trang 54 SGK Toán 12 Tập 1: Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho $\vec{A I} = 3 \vec{I G}$ (H.2.19). Chứng minh rằng $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$ .

Lời giải:

Theo ví dụ 8 ta có: $\vec{A B} + \vec{A C} + \vec{A D} = 3 \vec{A G}$ $\Rightarrow \vec{A I} + \vec{I B} + \vec{A I} + \vec{I C} + \vec{A I} + \vec{I D} = 3 \vec{A G}$

$\Rightarrow \vec{I B} + \vec{I C} + \vec{I D} = 3 \vec{A G} - 3 \vec{A I} = 3 (\vec{A G} + \vec{I A}) = 3 \vec{I G} = \vec{A I}$ $\Rightarrow \vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$

Vận dụng 8 trang 54 SGK Toán 12 Tập 1: Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ $\vec{F_{1}}$ và $\vec{F_{2}}$ . Hãy giải thích vì sao $\vec{F_{1}} = k \vec{F_{2}}$ với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải:

Vì trong quá trình máy bay tăng vận tốc từ 900km/h lên 920km/h máy bay giữ nguyên hướng bay nên vectơ $\vec{F_{1}}$ và $\vec{F_{2}}$ có cùng hướng. Do đó, $\vec{F_{1}} = k \vec{F_{2}}$ với k là một số thực dương nào đó (1).

Gọi $v_{1}, v_{2}$ lần lượt là vận tốc của của chiếc máy bay khi đạt 900km/h và 920km/h.

Suy ra $v_{1} = 900 (k m / h), v_{2} = 920 (k m / h)$

Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên

$\frac{| \vec{F_{1}} |}{| \vec{F_{2}} |} = \frac{v_{1}^{2}}{v_{2}^{2}} = \frac{900^{2}}{920^{2}} = \frac{2025}{2116} \Rightarrow | \vec{F_{1}} | = \frac{2025}{2116} | \vec{F_{2}} |$ (2)

Từ (1) và (2) ta có: $\vec{F_{1}} = \frac{2025}{2116} \vec{F_{2}} \Rightarrow k = \frac{2025}{2116} \approx 0, 96$

Hoạt động 7 trang 54 SGK Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Lấy điểm O và vẽ các vectơ $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ . Lấy điểm O’ khác O và vẽ các vectơ $\vec{O^{'} A^{'}} = \vec{a}, \vec{O^{'} B^{'}} = \vec{b}$ (H.2.21).

a) Hãy giải thích vì sao $\vec{A B} = \vec{A^{'} B^{'}}$ .

b) Áp dụng định lí côsin cho hai tam giác OAB và O’A’B’ để giải thích vì sao $\hat{A O B} = \hat{A^{'} O^{'} B^{'}}$

Lời giải:

a) Ta có: $\vec{A B} = \vec{A O} + \vec{O B}; \vec{A^{'} B^{'}} = \vec{A^{'} O^{'}} + \vec{O^{'} B^{'}}$

Mà $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}, \vec{O^{'} A^{'}} = \vec{a}, \vec{O^{'} B^{'}} = \vec{b} \Rightarrow \vec{A O} = \vec{A^{'} O^{'}}; \vec{O B} = \vec{O^{'} B^{'}}$

Do đó, $\vec{A B} = \vec{A^{'} B^{'}}$

b) Áp dụng định lí côsin vào tam giác AOB ta có: $\cos \hat{A O B} = \frac{O A^{2} + O B^{2} - A B^{2}}{2. O A . O B}$

Áp dụng định lí côsin vào tam giác A’O’B’ ta có: $\cos \hat{A^{'} O^{'} B^{'}} = \frac{O^{'} A^{' 2} + O^{'} B^{' 2} - A^{'} B^{' 2}}{2. O^{'} A^{'} . O^{'} B^{'}}$

Vì $\vec{A B} = \vec{A^{'} B^{'}} \Rightarrow A B = A^{'} B^{'}, \vec{A O} = \vec{A^{'} O^{'}} \Rightarrow O A = O^{'} A^{'}; \vec{O B} = \vec{O^{'} B^{'}} \Rightarrow O B = O^{'} B^{'}$

Do đó, $\cos \hat{A O B} = \cos \hat{A^{'} O^{'} B^{'}} \Rightarrow \hat{A O B} = \hat{A^{'} O^{'} B^{'}}$

Câu hỏi trang 55 SGK Toán 12 Tập 1: Xác định góc giữa hai vectơ cùng hướng (và khác $\vec{0}$ ), góc giữa hai vectơ ngược hướng trong không gian.

Lời giải:

Góc giữa hai vectơ cùng hướng bằng $0^{0}$ .

Góc giữa hai vectơ ngược hướng bằng $180^{0}$ .

Luyện tập 9 trang 56 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc $(\vec{A A^{'}}, \vec{B C})$ và $(\vec{A B}, \vec{A^{'} C^{'}})$ .

Lời giải:

Vì ABC.A’B’C’ là lăng trụ tam giác đều nên AA’B’B là hình chữ nhật. Suy ra, $\vec{A A^{'}} = \vec{B B^{'}}$ . Do đó: $(\vec{A A^{'}}, \vec{B C}) = (\vec{B B^{'}}, \vec{B C}) = \hat{B^{'} B C} = 90^{0}$ (do BB’C’C là hình chữ nhật)

Vì AA’B’B là hình chữ nhật nên $\vec{A B} = \vec{A^{'} B^{'}}$ .

Do đó, $(\vec{A B}, \vec{A^{'} C^{'}}) = (\vec{A^{'} B^{'}}, \vec{A^{'} C^{'}}) = \hat{C^{'} A^{'} B^{'}}$ .

Vì tam giác A’B’C’ là tam giác đều nên $\hat{C^{'} A^{'} B^{'}} = 60^{0}$ . Do đó, $(\vec{A B}, \vec{A^{'} C^{'}}) = 60^{0}$ .

Hoạt động 8 trang 56 SGK Toán 12 Tập 1: Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.

Lời giải:

Công thức xác định tích vô hướng của hai vectơ trong mặt phẳng: Tích vô hướng của hai vectơ $\vec{u}$ và $\vec{v}$ là một số, kí hiệu là $\vec{u} \cdot \vec{v}$ , được xác định bởi công thức sau:

$\vec{u} \cdot \vec{v} = | \vec{u} | \cdot | \vec{v} | \cdot \cos (\vec{u}, \vec{v})$ .

Luyện tập 10 trang 57 SGK Toán 12 Tập 1: Trong Ví dụ 10, hãy tính các tích vô hướng $\vec{A S} . \vec{B D}$ và $\vec{A S} . \vec{C D}$

Lời giải:

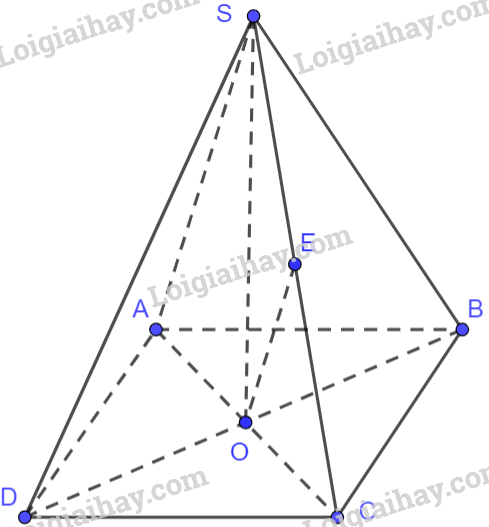
Gọi O là giao điểm của hai đường chéo AC và BD trong hình vuông ABCD. Do đó, O là trung điểm của BD, O là trung điểm của AC.

Tứ giác ABCD là hình vuông cạnh a nên độ dài đường chéo BD là $a \sqrt{2}$ $\Rightarrow O B = \frac{a \sqrt{2}}{2}$

Gọi E là trung điểm của SC. Mà O là trung điểm của AC nên OE là đường trung bình của tam giác SAC, do đó, OE//SA, $O E = \frac{1}{2} S A = \frac{a}{2}$ . Suy ra: $\vec{A S} = 2 \vec{O E}$

Vì O là trung điểm của BD nên $\vec{B D} = 2 \vec{O B}$

Vì tam giác SBC có ba cạnh bằng nhau nên tam giác SBC là tam giác đều. Do đó, BE là đường trung tuyến đồng thời là đường cao của tam giác SBC. Do đó, $E B = \frac{a \sqrt{3}}{2}$ .

Ta có: $O E^{2} + O B^{2} = \frac{a^{2}}{4} + \frac{a^{2}}{2} = \frac{3 a^{2}}{4} = E B^{2}$ nên $Δ$ EOB vuông tại O. Do đó, $\vec{O E} ⊥ \vec{O B}$

Ta có: $\vec{A S} . \vec{B D} = 2 \vec{O E} . (- 2 \vec{O B}) = - 4 \vec{O E} . \vec{O B} = 0$

Tứ giác ABCD là hình vuông nên $\vec{C D} = \vec{B A}$

Ta có: $\vec{A S} . \vec{C D} = \vec{A S} . \vec{B A} = - \vec{A S} . \vec{A B} = - | \vec{A S} | . | \vec{A B} | \cos (\vec{A S}, \vec{A B}) = - | \vec{A S} | . | \vec{A B} | \cos \hat{S A B}$

Vì tam giác SAB có ba cạnh bằng nhau nên tam giác SAB đều, suy ra $\hat{S A B} = 60^{0}$

Suy ra: $\vec{A S} . \vec{C D} = - | \vec{A S} | . | \vec{A B} | \cos \hat{S A B} = - a . a . \cos 60^{0} = \frac{- a^{2}}{2}$

Luyện tập 11 trang 57 SGK Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng $\vec{A^{'} C} . \vec{B^{'} D^{'}} = 0$ .

Lời giải:

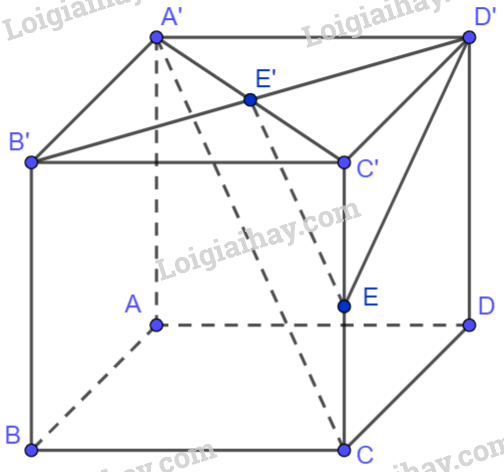
Giả sử cạnh của hình lập phương ABCD.A’B’C’D’ bằng 1. Khi đó, $A^{'} C^{'} = B^{'} D^{'} = \sqrt{2}$

Gọi E’ là giao điểm của hai đường chéo A’C’ và B’D’ của hình vuông A’B’C’D’. Khi đó, E’ là trung điểm của A’C’ và B’D’. Suy ra $\vec{B^{'} D^{'}} = 2 \vec{E^{'} D^{'}}$ và $E^{'} D^{'} = \frac{\sqrt{2}}{2}$ .

Gọi E là trung điểm của CC’. Mà E’ là trung điểm của A’C’ nên EE’ là đường trung bình của tam giác A’C’C. Do đó, $\vec{A^{'} C} = 2 \vec{E^{'} E}$ và $E^{'} E = \frac{1}{2} A^{'} C$

Áp dụng định lí Pythagore vào $Δ$ A’C’C vuông tại C’ có: $A^{'} C = \sqrt{A^{'} C^{' 2} + C^{'} C^{2}} = \sqrt{2 + 1} = \sqrt{3}$ $\Rightarrow E^{'} E = \frac{\sqrt{3}}{2}$

Áp dụng định lí Pythagore vào $Δ$ D’C’E vuông tại C’ có:

$E D^{' 2} = C^{'} D^{' 2} + C^{'} E^{2} = 1 + \frac{1}{4} = \frac{5}{4}$

Vì $E^{'} D^{' 2} + E^{'} E^{2} = \frac{1}{2} + \frac{3}{4} = \frac{5}{4} = E D^{' 2}$ nên $Δ$ E’D’E vuông tại E’. Do đó, $\vec{E^{'} E} ⊥ \vec{E^{'} D^{'}}$

Ta có: $\vec{A^{'} C} . \vec{B^{'} D^{'}} = 2. \vec{E^{'} E} .2 . \vec{E^{'} D^{'}}$ $= 0$ (đpcm)

Vận dụng 4 trang 57 SGK Toán 12 Tập 1: Như đã biết, nếu có một lực $\vec{F}$ tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức $A = \vec{F} . \vec{M N}$ , trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực $\vec{F}$ có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?

Lời giải:

Ta có: $A = \vec{F} . \vec{M N} = | \vec{F} | . | \vec{M N} | . \cos (\vec{F}, \vec{M N})$

Vì lực $\vec{F}$ có độ lớn không đổi và vật di chuyển một quãng đường không đổi nên A lớn nhất khi $\cos (\vec{F}, \vec{M N})$ lớn nhất. Do đó, $\cos (\vec{F}, \vec{M N}) = 1 \Leftrightarrow (\vec{F}, \vec{M N}) = 0^{0}$ . Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.

Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.

Bài 2.1 trang 58 SGK Toán 12 Tập 1: Trong không gian, cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ phân biệt và đều khác $\vec{0}$ . Những mệnh đề nào sau đây là đúng?

a) Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

b) Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

c) Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ ngược hướng.

d) Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ ngược hướng.

Lời giải:

Các câu đúng: Nếu $\vec{a}$ và $\vec{b}$ đều cùng hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

Nếu $\vec{a}$ và $\vec{b}$ đều ngược hướng với $\vec{c}$ thì $\vec{a}$ và $\vec{b}$ cùng hướng.

Bài 2.2 trang 58 SGK Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có

A B = 2, A D = 3

và

A A^{'} = 4

. Tính độ dài của các vectơ

\vec{B B^{'}}, \vec{B D}

và

\vec{B D^{'}}

Lời giải:

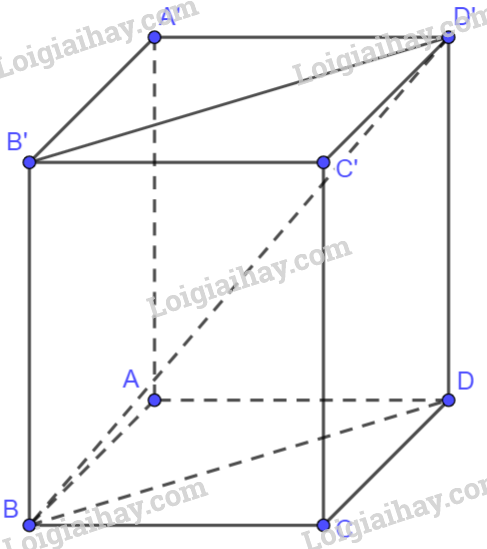
Vì B’BAA’ là hình chữ nhật nên $B B^{'} = A A^{'} = D D^{'} = 4 \Rightarrow | \vec{B B^{'}} | = 4$

Vì tứ giác ABCD là hình chữ nhật nên tam giác BAD vuông tại A.

Do đó, $B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{2^{2} + 3^{2}} = \sqrt{13}$ (định lí Pythagore), suy ra: $| \vec{B D} | = \sqrt{13}$

Vì BB’D’D là hình chữ nhật nên tam giác DD’B vuông tại D

Theo định lí Pythagore ta có: $B D^{'} = \sqrt{B D^{2} + D D^{' 2}} = \sqrt{13 + 4^{2}} = \sqrt{29} \Rightarrow | \vec{B D^{'}} | = \sqrt{29}$

Bài 2.3 trang 58 SGK Toán 12 Tập 1: Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ

\vec{a}

) phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ

\vec{b}, \vec{c}, \vec{d}, \vec{e}

a) Hãy chỉ ra mối quan hệ về phương và hướng của các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ và $\vec{e}$ .

b) Giải thích vì sao các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ đôi một bằng nhau.

Lời giải:

a) Các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ và $\vec{e}$ có cùng phương; các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ cùng hướng với nhau và ngược hướng với vectơ $\vec{e}$ .

b) Vì trọng lực tác dụng lên bàn phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn nên các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ có độ lớn bằng nhau. Mà các vectơ $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ cùng hướng với nhau. Do đó, các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ đôi một bằng nhau.

Bài 2.4 trang 58 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:

a) $\vec{A B} + \vec{D D^{'}} + \vec{C^{'} D^{'}} = \vec{C C^{'}}$ ;
b) $\vec{A B} + \vec{C D^{'}} - \vec{C C^{'}} = \vec{0}$ ;
c) $\vec{B C} - \vec{C C^{'}} + \vec{D C} = \vec{A^{'} C}$

Lời giải:

a) Vì ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$

Vì CDD’C’ là hình bình hành nên $\vec{C^{'} D^{'}} = \vec{C D}, \vec{D D^{'}} = \vec{C C^{'}}$

Ta có: $\vec{A B} + \vec{D D^{'}} + \vec{C^{'} D^{'}} = \vec{D C} + \vec{C C^{'}} + \vec{C D} = (\vec{C D} + \vec{D C}) + \vec{C C^{'}} = \vec{C C^{'}}$

b) Ta có: $\vec{A B} + \vec{C D^{'}} - \vec{C C^{'}} = \vec{A B} + \vec{C^{'} D^{'}} = \vec{A B} + \vec{C D} = \vec{0}$

c) Vì ABCD là hình bình hành nên $\vec{C B} + \vec{C D} = \vec{C A}$

Vì A’ACC’ là hình bình hành nên $\vec{C A} + \vec{C C^{'}} = \vec{C A^{'}}$

$\vec{B C} - \vec{C C^{'}} + \vec{D C} = - (\vec{C B} + \vec{C D}) - \vec{C C^{'}} = - \vec{C A} - \vec{C C^{'}} = - (\vec{C A} + \vec{C C^{'}}) = - \vec{C A^{'}} = \vec{A^{'} C}$

Bài 2.5 trang 58 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’ có

\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}

và

\vec{A C} = \vec{c}

. Hãy biểu diễn các vectơ sau qua các vectơ

\vec{a}, \vec{b}, \vec{c}

a) $\vec{A B^{'}}$ ;
b) $\vec{B^{'} C}$ ;
c) $\vec{B C^{'}}$ .

Lời giải:

a) Vì A’ABB’ là hình bình hành nên $\vec{A B^{'}} = \vec{A A^{'}} + \vec{A B} = \vec{a} + \vec{b}$

b) Vì A’ABB’ là hình bình hành nên $\vec{A A^{'}} = \vec{B B^{'}} = \vec{a}$

Ta có: $\vec{B C} = \vec{B A} + \vec{A C} = - \vec{b} + \vec{c}$

Vì C’CBB’ là hình bình hành nên

+ $\vec{B^{'} C^{'}} = \vec{B C} = - \vec{b} + \vec{c}$

+ $\vec{B^{'} C} = \vec{B^{'} C^{'}} + \vec{B^{'} B} = - \vec{b} + \vec{c} - \vec{a}$

c) Vì C’CBB’ là hình bình hành nên $\vec{B C^{'}} = \vec{B C} + \vec{B B^{'}} = - \vec{b} + \vec{c} + \vec{a}$

Bài 2.6 trang 58 SGK Toán 12 Tập 1: Cho hình chóp tứ giác S. ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu

\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}

Lời giải:

Chứng minh: Nếu tứ giác ABCD là hình bình hành thì $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Gọi O là tâm hình bình hành ABCD. Khi đó, O là trung điểm của AC, BD.

Suy ra $\vec{O C} = - \vec{O A}, \vec{O D} = - \vec{O B}$

Ta có: $\vec{S A} + \vec{S C} = \vec{S O} + \vec{O A} + \vec{S O} + \vec{O C} = 2 \vec{S O} + (\vec{O A} - \vec{O A}) = 2 \vec{S O}$

$\vec{S B} + \vec{S D} = \vec{S O} + \vec{O B} + \vec{S O} + \vec{O D} = 2 \vec{S O} + (\vec{O B} - \vec{O B}) = 2 \vec{S O}$

Do đó, $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Chứng minh: Nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ thì tứ giác ABCD là hình bình hành:

Ta có: $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D} \Leftrightarrow \vec{S A} - \vec{S B} = \vec{S D} - \vec{S C} \Leftrightarrow \vec{B A} = \vec{C D}$

Suy ra, hai vectơ $\vec{B A}$ và $\vec{C D}$ cùng hướng và có độ lớn bằng nhau.

Suy ra, $A B = C D,$ AB//CD. Khi đó, tứ giác ABCD là hình bình hành.

Vậy tứ giác ABCD là hình bình hành nếu và chỉ nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Bài 2.7 trang 58 SGK Toán 12 Tập 1: Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho $S M = 2 A M$ . Trên cạnh BC, lấy điểm N sao cho $C N = 2 B N$ . Chứng minh rằng $\vec{M N} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ .

Lời giải:

Ta có: $\vec{M N} = \vec{M A} + \vec{A C} + \vec{C N} = \frac{1}{3} \vec{S A} + \vec{A B} + \vec{B C} + \frac{2}{3} \vec{C B}$

$= \frac{1}{3} \vec{S A} + \vec{B C} - \frac{2}{3} \vec{B C} + \vec{A B} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ (đpcm)

Ta có: $\vec{M N} = \vec{M A} + \vec{A C} + \vec{C N} = \frac{1}{3} \vec{S A} + \vec{A B} + \vec{B C} + \frac{2}{3} \vec{C B}$

$= \frac{1}{3} \vec{S A} + \vec{B C} - \frac{2}{3} \vec{B C} + \vec{A B} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ (đpcm)

Bài 2.8 trang 58 SGK Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn

\vec{A I} = 3 \vec{I G}

, ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8cm (H.2.30).

Lời giải:

Đặt tên khối rubik là tứ diện đều ABCD có G là trọng tâm tam giác BCD, I là trọng tâm tứ diện ABCD. Do đó, $\vec{A I} = 3 \vec{I G} \Rightarrow I G = \frac{1}{4} A G$

Vì chiều cao của rubik bằng 8cm nên $A G = 8 c m \Rightarrow I G = \frac{1}{4} .8 = 2 (c m)$

Vậy khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó bằng 2cm.

Bài 2.9 trang 58 SGK Toán 12 Tập 1: Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.

Lời giải:

Biểu diễn lực các lực kéo của ba sợi dây bằng các vectơ, đặt tên các vectơ như hình vẽ:

Lấy điểm D sao cho tứ giác DCAE là hình bình hành (điểm D nằm khác phía với điểm B).

Do đó, giá của các vectơ $\vec{A C}$ và $\vec{A E}$ cùng nằm trên mặt phẳng (ACDE). (1)

Vì DCAE là hình bình hành nên $\vec{A C} + \vec{A E} = \vec{A D}$ (quy tắc hình bình hành)

Vì các lực kéo làm cho ba sợi dây ở trạng thái đứng yên nên $\vec{A D} = - \vec{A B}$ , do đó hai vectơ $\vec{A D}$ và $\vec{A B}$ có giá cùng nằm trên một mặt phẳng (ACDE). (2)

Từ (1) và (2) suy ra ba vectơ $\vec{A C}$ , $\vec{A E}$ và $\vec{A B}$ có giá cùng nằm trên mặt phẳng (ACDE).

Vậy khi các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng

Bài 2.10 trang 58 SGK Toán 12 Tập 1: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:

a) $\vec{A A^{'}}$ và $\vec{C^{'} C;}$
b) $\vec{A A^{'}}$ và $\vec{B C;}$
c) $\vec{A C}$ và $\vec{B^{'} A^{'}}$ .

Lời giải:

a) Vì AA’//CC’ nên hai vectơ $\vec{A A^{'}}$ và $\vec{C^{'} C}$ ngược hướng nhau.

Suy ra, $(\vec{A A^{'}}, \vec{C^{'} C}) = 180^{0}$ .

Do đó, $\vec{A A^{'}} . \vec{C^{'} C} = | \vec{A A^{'}} | . | \vec{C^{'} C} | . \cos (\vec{A A^{'}}, \vec{C^{'} C}) = 2.2. \cos 180^{0} = - 4$

b) Vì A’ADD’ là hình chữ nhật nên $\hat{A^{'} A D} = 90^{0}$

Vì ABCD là hình vuông nên $\vec{B C} = \vec{A D}$ . Do đó, $(\vec{A A^{'}}, \vec{B C}) = (\vec{A A^{'}}, \vec{A D}) = \hat{A^{'} A D} = 90^{0}$

Ta có: $\vec{A A^{'}} . \vec{B C} = \vec{A A^{'}} . \vec{A D} = | \vec{A A^{'}} | . | \vec{A D} | . \cos (\vec{A A^{'}}, \vec{A D}) = 2.1. \cos 90^{0} = 0$

c) Vì A’ABB’ là hình chữ nhật nên $\vec{B^{'} A^{'}} = \vec{B A}$ .

Vì ABCD là hình vuông nên $\hat{C A B} = 45^{0}$ và $A C = \sqrt{2}$

Ta có: $\vec{A C} . \vec{B^{'} A^{'}} = - \vec{A C} . \vec{A B} = - | \vec{A C} | . | \vec{A B} | . \cos (\vec{A C}, \vec{A B}) = - \sqrt{2} .1 . \cos 45^{0} = - 1$

Bài 2.11 trang 58 SGK Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ có cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là $45^{0}$ , hãy tính:
a) $\vec{a} . \vec{b}$ ;
b) $(\vec{a} + 3 \vec{b}) . (\vec{a} - 2 \vec{b})$
c) ${(\vec{a} + \vec{b})}^{2}$ .

Lời giải:

a) $\vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos (\vec{a}, \vec{b}) = 1.1. \cos 45^{0} = \frac{\sqrt{2}}{2}$

b) $(\vec{a} + 3 \vec{b}) . (\vec{a} - 2 \vec{b}) = {\vec{a}}^{2} + \vec{a} . \vec{b} - 6 {\vec{b}}^{2} = 1 + \frac{\sqrt{2}}{2} - 6.1 = - 5 + \frac{\sqrt{2}}{2}$

c) ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} = 1 + 2. \frac{\sqrt{2}}{2} + 1 = 2 + \sqrt{2}$

Bài 2.12 trang 58 SGK Toán 12 Tập 1: Cho tứ diện ABCD. Chứng minh rằng:

a) $\vec{A B} . \vec{C D} = \vec{A C} . \vec{C D} + \vec{B C} . \vec{D C}$ ;
b) $\vec{A B} . \vec{C D} + \vec{A C} . \vec{D B} + \vec{A D} . \vec{B C} = 0$ .

Lời giải:

a) Ta có: $\vec{A C} . \vec{C D} + \vec{B C} . \vec{D C} = \vec{A C} . \vec{C D} - \vec{B C} . \vec{C D} = \vec{C D} (\vec{A C} + \vec{C B}) = \vec{C D} . \vec{A B}$ (đpcm)

b) $\vec{A B} . \vec{C D} + \vec{A C} . \vec{D B} + \vec{A D} . \vec{B C} = \vec{A B} . \vec{C D} + (\vec{A B} + \vec{B C}) . \vec{D B} + (\vec{A B} + \vec{B D}) . \vec{B C}$

$= \vec{A B} . \vec{C D} + \vec{A B} . \vec{D B} + \vec{B C} . \vec{D B} + \vec{A B} . \vec{B C} + \vec{B D} . \vec{B C}$

$= \vec{A B} . (\vec{C D} + \vec{D B} + \vec{B C}) + (\vec{B C} . \vec{D B} + \vec{B D} . \vec{B C}) = \vec{A B} . (\vec{C B} + \vec{B C}) + \vec{B C} (\vec{D B} + \vec{B D}) = 0$