Bài 2.6 trang 58 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Bài 2.6 trang 58 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Mai Hương Ngày: 15-03-2024 Lớp 12

108

Với giải Bài 2.6 trang 58 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 6: Vectơ trong không gian giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Bài 2.6 trang 58 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Bài 2.6 trang 58 SGK Toán 12 Tập 1: Cho hình chóp tứ giác S. ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ .

Lời giải:

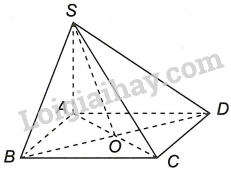
Chứng minh: Nếu tứ giác ABCD là hình bình hành thì $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Gọi O là tâm hình bình hành ABCD. Khi đó, O là trung điểm của AC, BD.

Suy ra $\vec{O C} = - \vec{O A}, \vec{O D} = - \vec{O B}$

Ta có: $\vec{S A} + \vec{S C} = \vec{S O} + \vec{O A} + \vec{S O} + \vec{O C} = 2 \vec{S O} + (\vec{O A} - \vec{O A}) = 2 \vec{S O}$

$\vec{S B} + \vec{S D} = \vec{S O} + \vec{O B} + \vec{S O} + \vec{O D} = 2 \vec{S O} + (\vec{O B} - \vec{O B}) = 2 \vec{S O}$

Do đó, $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Chứng minh: Nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ thì tứ giác ABCD là hình bình hành:

Ta có: $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D} \Leftrightarrow \vec{S A} - \vec{S B} = \vec{S D} - \vec{S C} \Leftrightarrow \vec{B A} = \vec{C D}$

Suy ra, hai vectơ $\vec{B A}$ và $\vec{C D}$ cùng hướng và có độ lớn bằng nhau.

Suy ra, $A B = C D,$ AB//CD. Khi đó, tứ giác ABCD là hình bình hành.

Vậy tứ giác ABCD là hình bình hành nếu và chỉ nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Hoạt động 1 trang 46 SGK Toán 12 Tập 1: Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.

Câu hỏi trang 46 SGK Toán 12 Tập 1: Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Luyện tập 1 trang 47 SGK Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ $\vec{A C}, \vec{A D}, \vec{A D^{'}}$ :

Hoạt động 2 trang 47 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.7) a) So sánh độ dài hai vectơ $\vec{A B}$ và $\vec{D^{'} C^{'}}$ .

Câu hỏi trang 47 SGK Toán 12 Tập 1: Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?

Luyện tập 2 trang 48 SGK Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.

Vận dụng 1 trang 48 SGK Toán 12 Tập 1: Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29.

Hoạt động 3 trang 49 SGK Toán 12 Tập 1:Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Lấy điểm A và vẽ các vectơ $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ .

Luyện tập 3 trang 50 SGK Toán 12 Tập 1: Trong Ví dụ 3, hãy tính độ dài của vectơ $\vec{A C} + \vec{C^{'} D^{'}}$ .

Luyện tập 4 trang 50 SGK Toán 12 Tập 1: Cho tứ diện ABCD (H.2.13). Chứng minh rằng $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$ .

Hoạt động 4 trang 50 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.14). a) Hai vectơ $\vec{A B} + \vec{A D}$ và $\vec{A C}$ có bằng nhau hay không?

Câu hỏi trang 50 SGK Toán 12 Tập 1: Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.

Luyện tập 5 trang 50 SGK Toán 12 Tập 1: Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng $\vec{B B^{'}} + \vec{C D} + \vec{A D} = \vec{B D^{'}}$

Hoạt động 5 trang 51 SGK Toán 12 Tập 1: Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa.

Luyện tập 6 trang 52 SGK Toán 12 Tập 1: Trong Ví dụ 6, chứng minh rằng: a) $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau;

Vận dụng 2 trang 52 SGK Toán 12 Tập 1: Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống.

Hoạt động 6 trang 52 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)

Câu hỏi trang 53 SGK Toán 12 Tập 1: Hai vectơ $1 \vec{a}$ và $\vec{a}$ có bằng nhau không? Hai vectơ $(- 1) \vec{a}$ và $- \vec{a}$ có bằng nhau không?

Luyện tập 7 trang 53 SGK Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho $S E = \frac{1}{3} S A, S F = \frac{1}{3} S B$ . Chứng minh rằng $\vec{E F} = \frac{1}{3} \vec{D C}$ .

Luyện tập 8 trang 54 SGK Toán 12 Tập 1: Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho $\vec{A I} = 3 \vec{I G}$ (H.2.19). Chứng minh rằng $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$ .

Vận dụng 8 trang 54 SGK Toán 12 Tập 1: Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20).

Hoạt động 7 trang 54 SGK Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Lấy điểm O và vẽ các vectơ $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ .

Câu hỏi trang 55 SGK Toán 12 Tập 1: Xác định góc giữa hai vectơ cùng hướng (và khác $\vec{0}$ ), góc giữa hai vectơ ngược hướng trong không gian.

Luyện tập 9 trang 56 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc $(\vec{A A^{'}}, \vec{B C})$ và $(\vec{A B}, \vec{A^{'} C^{'}})$ .

Hoạt động 8 trang 56 SGK Toán 12 Tập 1: Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.

Luyện tập 10 trang 57 SGK Toán 12 Tập 1: Trong Ví dụ 10, hãy tính các tích vô hướng $\vec{A S} . \vec{B D}$ và $\vec{A S} . \vec{C D}$

Luyện tập 11 trang 57 SGK Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng $\vec{A^{'} C} . \vec{B^{'} D^{'}} = 0$ .

Vận dụng 4 trang 57 SGK Toán 12 Tập 1: Như đã biết, nếu có một lực $\vec{F}$ tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức $A = \vec{F} . \vec{M N}$

Bài 2.1 trang 58 SGK Toán 12 Tập 1: Trong không gian, cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ phân biệt và đều khác $\vec{0}$ . Những mệnh đề nào sau đây là đúng?

Bài 2.2 trang 58 SGK Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có

A B = 2, A D = 3

A A^{'} = 4

. Tính độ dài của các vectơ

\vec{B B^{'}}, \vec{B D}

\vec{B D^{'}}

.

Bài 2.3 trang 58 SGK Toán 12 Tập 1: Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29.

Bài 2.4 trang 58 SGK Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:

Bài 2.5 trang 58 SGK Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’ có

\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}

\vec{A C} = \vec{c}

. Hãy biểu diễn các vectơ sau qua các vectơ

\vec{a}, \vec{b}, \vec{c}

:

Bài 2.6 trang 58 SGK Toán 12 Tập 1: Cho hình chóp tứ giác S. ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu

\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}

Bài 2.7 trang 58 SGK Toán 12 Tập 1: Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho $S M = 2 A M$ . Trên cạnh BC, lấy điểm N sao cho $C N = 2 B N$ .

Bài 2.8 trang 58 SGK Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn

\vec{A I} = 3 \vec{I G}

, ở đó G là trọng tâm của tam giác BCD.

Bài 2.9 trang 58 SGK Toán 12 Tập 1: Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31).

Bài 2.10 trang 58 SGK Toán 12 Tập 1: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2.

Bài 2.11 trang 58 SGK Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ có cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là $45^{0}$

Bài 2.12 trang 58 SGK Toán 12 Tập 1: Cho tứ diện ABCD. Chứng minh rằng: a)

\vec{A B} . \vec{C D} = \vec{A C} . \vec{C D} + \vec{B C} . \vec{D C}

;

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 12

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

205

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

219

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.