Với giải Câu hỏi trang 119 Toán 10 Tập 1 Chân trời sáng tạo trong Bài 3: Các số đặc trưng đô xu thế trung tâm của mẫu dữ liệu giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 119 Bài 3: Các số đặc trưng đô xu thế trung tâm của mẫu dữ liệu
|
Năm |
Tổng điểm |
Năm |
Tổng điểm |
Năm |
Tổng điểm |
Năm |
Tổng điểm |
|
2020 |
150 |
2015 |
151 |
2010 |
133 |
2005 |
143 |
|
2019 |
177 |
2014 |
157 |
2009 |
161 |
2004 |
196 |
|
2018 |
148 |
2013 |
180 |
2008 |
159 |
2003 |
172 |
|
2017 |
155 |
2012 |
148 |
2007 |
168 |
2002 |
166 |
|
2016 |
151 |
2011 |
113 |
2006 |
131 |
2001 |
139 |
(Nguồn: https://imo-offial.org)
Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không.
Phương pháp giải
+) Số trung bình:
+) Trung vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2: Tình trung vị:
Lời giải
+) Giai đoạn 2001 – 2010
Số trung bình
Sắp sếp số liệu theo thứ tự không giảm, ta được:
Do , là số chẵn nên trung vị là:
+) Giai đoạn 2011 – 2020
Số trung bình
Sắp sếp số liệu theo thứ tự không giảm, ta được:
Do , là số chẵn nên trung vị là:
+) So sánh theo số trung bình hay số trung vị ta đều thấy điểm thi của đổi tuyển giai đoạn 2001 – 2010 cao hơn giai đoạn 2011 – 2020.
Vậy ý kiến trên là đúng.
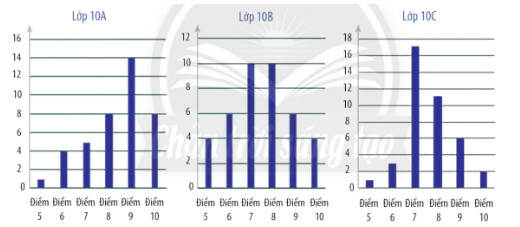
a) Hãy lập thống kê số lượng học sinh theo điểm số ở mỗi lớp.
b) Hãy so sánh điểm số của học sinh các lớp đó theo số trung bình, trung vị và mốt.
Phương pháp giải
b)
+) Số trung bình:
+) Trung vị:
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm:
Bước 2: Tình trung vị:
+) Mốt là giá trị có tần số lớn nhất. (Một mẫu có thể có nhiều mốt)
Lời giải
a)
|
Lớp 10A |
Điểm |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số HS |
1 |
4 |
5 |
8 |
14 |
8 |
|
|
Lớp 10B |
Điểm |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số HS |
4 |
6 |
10 |
10 |
6 |
4 |
|
|
Lớp 10C |
Điểm |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số HS |
1 |
3 |
17 |
11 |
6 |
2 |
b)
+) Lớp 10A
Số trung bình
Sắp sếp số liệu theo thứ tự không giảm, ta được:
Do , là số chẵn nên trung vị là:
Mốt
+) Lớp 10B
Số trung bình
Sắp sếp số liệu theo thứ tự không giảm, ta được:
Do , là số chẵn nên trung vị là:
Mốt
+) Lớp 10C
Số trung bình
Sắp sếp số liệu theo thứ tự không giảm, ta được:
Do , là số chẵn nên trung vị là:
Mốt
+) So sánh:
Số trung bình: => Điểm số của HS các lớp theo thứ tự giảm dần là 10A, 10C, 10B.
Số trung vị: => Điểm số của HS các lớp theo thứ tự giảm dần là 10A, 10B, 10C.
Mốt: Lớp 10A có 14 điểm 9, Lớp 10B có 10 điểm 7 và 10 điểm 8, Lớp 10C có 17 điểm 7. Do đó so sánh theo mốt thì điểm số các lớp giảm dàn theo thứ tự là: 10A, 10B, 10C.
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 115 Toán 10 Tập 1: Hãy tìm trung vị của các số liệu ở Vận dụng 1 và Vận dụng 2...
Thực hành 2 trang 117 Toán 10 Tập 1: Hãy tìm tứ phân vị của các mẫu số liệu sau...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.