Với giải Câu hỏi trang 19 SBT Toán 10 Tập 2 Chân trời sáng tạo trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
Nội dung bài viết
SBT Toán 10 Chân trời sáng tạo trang 23: Bài tập cuối chương 7
Bài 9 trang 23 SBT Toán 10: Một người phát cầu qua lưới từu độ cao y0 mét, nghiệm một góc α so với phương ngang với vận tốc đầu v0
Phương trình chuyển động của quả cầu là:
y=−g2v20cos2αx2+tan(α)x+y0 vớig=10 m/s2
Viết phương trình chuyển động của quả cầu nếu α=45∘,y0=0,3 m và v0=7,67 m/s
b) Để cầu qua được lưới bóng cao 1,5 m thì người phát cầu phải đứng cách lưới bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Lời giải:
a) Thay các số đã biết vào phương trình chuyển động ta có :
y=−102.7,672cos245∘x2+(tan45∘)x+0,3≃−0,17x2+x+0,3
b) Để cầu qua được lưới bóng cao 1,5 mét thì y>1,5⇔−0,17x2+x+0,3>1,5⇔−0,17x2+x+−1,2>0
Giải bất phương trình trên ta có tập nghiệm là (1,68;4,2)
Vậy người phát cầu phải đứng cách lưới khoảng 1,68 m đến 4,2 m
Bài 10 trang 22 SBT Toán 10: Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có AB=x;BC=5 và BD=6
a) Biểu diễn độ dài cạnh AC và AD theo x
b) Tìm x để chu vi của tam giác ABC là 12
c) Tìm x để AD=2AC
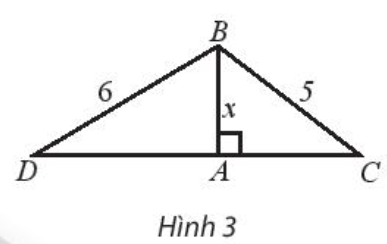
Lời giải:
a) Áp dụng định lí pitago cho tam giác ABC ta có:
AC=√BC2−AB2=√52−x2=√25−x2
Áp dụng định lí pitago cho tam giác ABD ta có:
AD=√BD2−AB2=√62−x2=√36−x2
b) Ta có: AB+AC+BC=12
⇔x+√25−x2+5=12⇔√25−x2=7−x⇒25−x2=49−14x+x2⇒2x2−14x+24=0
⇒x=3 hoặc x=4
Thay hai giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn
Vậy khi x=3 hoặc x=4 thì chu vi của tam giác ABC là 12
c) Ta có: AD=2AC
⇔√36−x2=2√25−x2⇒36−x2=4(25−x2)⇒3x2−64=0
⇒x=−8√33 (loại vì x>0) hoặc x=8√33
Thay x=8√33 vào phương trình ban đầu ta thấy thỏa mãn
Vậy x=8√33 thì AD=2AC
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 19 SBT Toán 10: Tam thức bậc hai nào có biệt thức Δ=1 và hai nghiệm là:x1=32 và x2=74?...
Câu 2 trang 19 SBT Toán 10: Tam thức bậc hai nào dương với mọi x∈R?...
Câu 3 trang 19 SBT Toán 10: Khẳng định nào sau đây đúng với tam thức bậc hai f(x)=10x2−3x−4?...
Câu 4 trang 19 SBT Toán 10: Trong trường hợp nào tam thức bậc hai f(x)=ax2+bx+c có Δ>0 và a<0?....
Câu 5 trang 20 SBT Toán 10: Cho đồ thị của hàm số bậc haiy = f(x) như hình 1....
Câu 6 trang 20 SBT Toán 10: Bất phương trình nào có tập nghiệm là (2;5)?...
Câu 7 trang 20 SBT Toán 10: Tập xác định của hàm số y=1√9x2−3x−2+√3−xlà....
Câu 8 trang 20 SBT Toán 10: Với giá trị nào của tham số m thì phương trình (2m+6)x2+4mx+3=0....
Câu 9 trang 20 SBT Toán 10: Giá trị nào là nghiệm của phương trình √x2+x+11=√−2x2−13x+16?....
Câu 10 trang 20 SBT Toán 10: Khẳng định nào đúng với phương trình √2x2−3x−1=√3x2−2x−13...
Câu 11 trang 21 SBT Toán 10: Khẳng định nào đúng với phương trình √5x2+27x+36= ?...
Câu 12 trang 21 SBT Toán 10: Cho đồ thị của hai hàm số bậc hai ...
Bài 1 trang 21 SBT Toán 10: Dựa vào đồ thị của hàm số bậc hai y= f(x) sau đây....
Bài 2 trang 21 SBT Toán 10: Xét dấu của các tam thức bậc hai sau: a) ....
Bài 3 trang 21 SBT Toán 10: Giải các phương trình bậc hai sau: a) ...
Bài 4 trang 22 SBT Toán 10: Dựa vào đồ thị của hàm số bậc hai được cho...
Bài 5 trang 22 SBT Toán 10: Giải các phương trình sau: a) ...
Bài 6 trang 22 SBT Toán 10: Tìm tập xác định của các hàm số sau: a) ....
Bài 7 trang 22 SBT Toán 10: Tìm các giá trị của tham số m để: a) là một tam thức bậc hai âm với mọi ...
Bài 8 trang 22 SBT Toán 10: Người ta thử nghiệm ném một quả bóng trên Mặt Trăng....
Bài 9 trang 23 SBT Toán 10: Một người phát cầu qua lưới từu độ cao...
Bài 10 trang 23 SBT Toán 10: Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có Ab = x; BC = 5 và BD = 6...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.