Với giải Câu hỏi trang 41 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Hàm số và đồ thị giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 47 Bài 1: Hàm số và đồ thị
Bài 1 trang 47 Toán 10 Tập 1: Tìm tập xác định của các hàm số sau:
a)
b)
Phương pháp giải
Tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức có nghĩa.
a) có nghĩa
b) có nghĩa
Lời giải
a) Biểu thức có nghĩa khi và chỉ khi tức là khi
Vậy tập xác định của hàm số này là
b) Biểu thức có nghĩa khi và chỉ khi tức là khi
Vậy tập xác định của hàm số này là
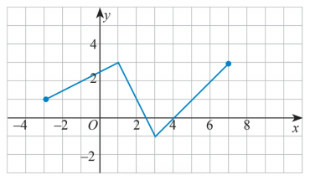
Bài 2 trang 47 Toán 10 Tập 1: Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
Phương pháp giải
+) Tập xác định là tập hợp các giá trị của biến số x.
+) Tập giá trị là tập hợp các giá trị y (tương ứng với x thuộc tập xác định)
Lời giải
Từ đồ thị, ta có:
Đồ thị hàm số xác định (liền mạch) từ đến , do đó tập xác định của hàm số là
Tập giá trị , vậy
Bài 3 trang 47 Toán 10 Tập 1: Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a)
b)
Phương pháp giải
Bước 1: Lấy là hai số tùy ý sao cho .
Bước 2: Tìm điều kiện để và
a)
b)
Bước 3: Kết luận khoảng đồng biến, nghịch biến
+ với thì hàm số đồng biến trên khoảng
+ với thì hàm số nghịch biến trên khoảng
Lời giải
a) Xét hàm số xác định trên
Lấy là hai số tùy ý sao cho .
Do nên , suy ra
Từ đây ta có
Vậy hàm số ngịch biến (giảm) trên
b) Xét hàm số xác định trên
+ Trên khoảng lấy là hai số tùy ý sao cho ., ta có:
Do nên và do nên .
Từ đây suy ra hay
Vậy hàm số nghịch biến (giảm) trên khoảng
+ Trên khoảng lấy là hai số tùy ý sao cho ., ta có:
Do nên và do nên .
Từ đây suy ra hay
Vậy hàm số đồng biến (tăng) trên khoảng
Bài 4 trang 47 Toán 10 Tập 1: Vẽ đồ thị hàm số biết rằng hàm số này còn được viết như sau:
Phương pháp giải
Vẽ đồ thị từng hàm trên mỗi khoảng cho trước
Lời giải
Hàm số xác định trên
Trên khoảng ta vẽ đồ thị hàm số , đi qua 2 điểm
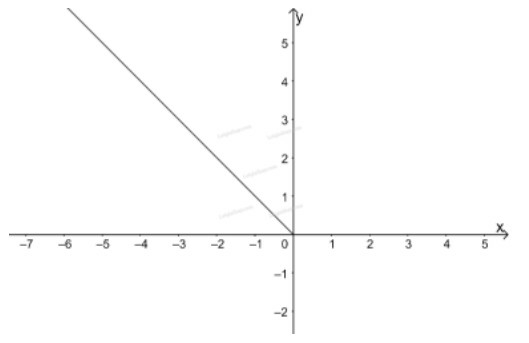
Trên khoảng ta vẽ đồ thị hàm số , đi qua 2 điểm
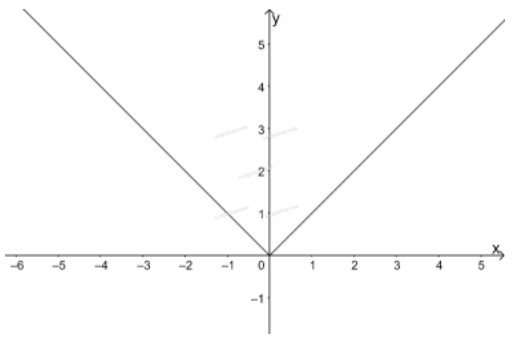
Như vậy ta được đồ thị hàm số .
Bài 5 trang 47 Toán 10 Tập 1: Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
Phương pháp giải
+) Tập xác định là tập hợp các giá trị của x để f(x) có nghĩa.
+) Tập giá trị là tập hợp các giá trị của f(x) với x thuộc tập xác định.
+) Vẽ đồ thị từng hàm trên mỗi khoảng cho trước
Lời giải
+) Dễ thấy: hàm số được xác định với mọi và .
Do đó tập xác định của hàm số là
+) Với :
+ Nếu thì
+ Nếu thì
Vậy tập giá trị của hàm số là
+) Vẽ đồ thị hàm số:
Với đồ thị hàm số là đường thẳng
Với đồ thị hàm số là đường thẳng
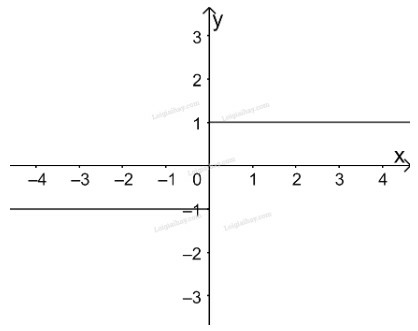
Ta được đồ thị hàm số như hình trên.
Bài 6 trang 47 Toán 10 Tập 1: Một hãng taxi có bảng giá như sau:
|
|
Giá mở cửa (0,5 km) |
Giá cước các kilomet tiếp theo |
Giá cước từ kilomet thứ 31 |
|
Taxi 4 chỗ |
11 000 đồng |
14 500 đồng |
11 600 đồng |
|
Taxi 7 chỗ |
11 000 đồng |
15 500 đồng |
13 600 đồng |
a) Xem số tiền đi taxi là một hàm số phụ thuộc số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
i) Hàm số để tính số tiền hành khách phải trả khi di chuyển km bằng xe taxi 4 chỗ.
ii) Hàm số để tính số tiền hành khách phải trả khi di chuyển km bằng xe taxi 7 chỗ.
b) Nếu cần đặt xe taxi cho 30 hành khách, nên đặt toàn bộ xe 4 chỗ hay xe 7 chỗ thì có lợi hơn?
Phương pháp giải
a) Viết công thức tính tiền trong mỗi trường hợp (theo số km), từ đó suy ra hàm số nhiều công thức tương ứng.
b) Tính số tiền phải trả trong mỗi trường hợp, từ đó đưa ra lời khuyên về chọn xe.
Lời giải
a)
i)
Nếu thì số tiền phải trả là đồng.
Nếu thì số tiền phải trả là đồng.
Vậy hàm số
ii)
Nếu thì số tiền phải trả là đồng.
Nếu thì số tiền phải trả là đồng.
Vậy hàm số
b)
Nếu đặt toàn bộ xe 4 chỗ cho 30 hành khách thì cần 8 xe.
Nếu đặt toàn bộ xe 7 chỗ cho 30 hành khách thì cần 5 xe.
So sánh số tiền dựa theo số kilomet di chuyển: Giả sử các hành khách cần di chuyển x kilomet
+) Nếu
Số tiền trả cho 8 xe taxi 4 chỗ là:
Số tiền trả cho 5 xe taxi 7 chỗ là:
Vì nên chọn 5 xe taxi 7 chỗ sẽ lợi hơn.
+) Nếu
Số tiền trả cho 8 xe taxi 4 chỗ là:
Số tiền trả cho 5 xe taxi 7 chỗ là:
Vì nên chọn 5 xe taxi 7 chỗ sẽ lợi hơn.
Kết luận: Nên đặt toàn bộ xe 7 chỗ thì có lợi hơn.

Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Lời giải
Sau khi vào hộp đen, x đi qua:
+) Đầu tiên, x đi qua hộp màu vàng (bình phương), ta được
+) Tiếp tục, đi qua hộp màu xanh lá (tăng gấp ba lần), ta được
+) Cuối cùng, đi qua hộp màu xanh dương (bớt đi 5), ta được:
Như vậy sau khi đi qua HỘP ĐEN, số x đã biến đổi thành số
Kiểm tra lại với số 2: theo công thức thì sau khi qua hộp đen ta được số: (đúng).
Vậy biểu thức f(x) mô tả sự biến đổi đã tác động lên x là:
Xem thêm các lời giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động Khởi động trang 41 Toán 10 Tập 1: Nhiệt độ có mối liên hệ gì với thời gian?...
Hoạt động Khám phá 2 trang 43 Toán 10 Tập 1: Xét hàm số cho bởi bảng sau...
Câu hỏi trang 44 Toán 10 Tập 1: Vẽ đồ thị hàm số ...
Bài 1 trang 47 Toán 10 Tập 1: Tìm tập xác định của các hàm số sau..
Bài 2 trang 47 Toán 10 Tập 1: Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10...
Bài 3 trang 47 Toán 10 Tập 1: Tìm các khoảng đồng biến, nghịch biến của các hàm số sau...
Bài 4 trang 47 Toán 10 Tập 1: Vẽ đồ thị hàm số biết rằng hàm số này còn được viết như sa....
Bài 5 trang 47 Toán 10 Tập 1: Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số...
Bài 6 trang 47 Toán 10 Tập 1: Một hãng taxi có bảng giá như sau...
Xem thêm các bài giải SGK Toán học lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 0 đến 180
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.