Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 100) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 100)
Câu 1: Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính sin^ACB,tan^ACB
Lời giải:
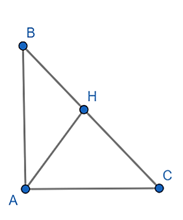
Áp dụng Pytago vào tam giác ABC vuông tại A có: BC2 = AB2 + AC2
Ta có: sin^ACB=ABBC=AB√AB2+AC2=AB√AB2+(3AB2)2=2√1313AB
tan^ACB=ABAC=23ACAC=23.
Câu 2: Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, ˆB=60° . Bán kính đường tròn nội tiếp tam giác ABC là r=2√3 cm. Tính đường cao AH của tam giác ABC.
Lời giải:
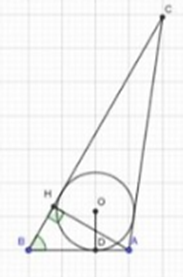
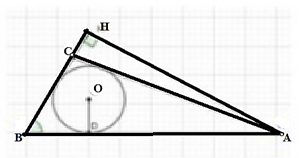
Đặt AB = c, AC = b, BC = a
Ta có: cosˆB=a2+c2−b22ac=112−2ac−b22ac
⇔ 12=112−2ac−b22ac
⇔ ac = 112 – 2ac – b2
⇔ 3ac = 112 – b2 (1)
Lại có: r=2SABCa+b+c=2.12.a.c.sinˆB11+b=√32ac11+b
⇔ 2√3=√32ac11+b
⇔ 43(11+b)=ac(2)
Từ (1) và (2): 4(11 + b) = (11 + b)(11 – b)
⇔ (11 + b)(4 – 11 + b) = 0
⇔ b = 7 (vì b > 0)
Suy ra: ac = 24
Mà a + c = 11
⇒ [{a=3c=8{a=8c=3
Suy ra: SABC=12(a+b+c).r=12.(11+7).2√3=18√3
Lại có: SABC=12.AH.BC⇒AH=2SABCBC
Nếu a = 8 thì AH=2.18√38=3√32
Nếu a = 3 thì AH=2.18√33=4√3 .
Câu 3: Cho C = 5 + 52 + … + 520. Chứng minh rằng C chia hết cho 5, 6, 13.
Lời giải:
a) Ta có C = 5 + 52 + … + 520
= 5(1 + 5 + 52 + ... + 519) ⋮ 5
Vậy C ⋮ 5.
b) Ta có C = 5 + 52 + … + 520
= (5 + 52) + 52(5 + 52) + ... + 518(5 + 52)
= 30 + 52.30 + ... + 518.30
= 30(1 + 52 + ... + 518)
= 5.6.(1 + 52 + ... + 518) ⋮ 6
Vậy C ⋮ 6.
c) Ta có C = (5 + 52 + 53 + 54) + (55 + 56 + 57 + 58) +... + (517 + 518 + 519 + 520)
= (5 + 52 + 53 + 54) + 54(5 + 52 + 53 + 54) + ... + 516(5 + 52 + 53 + 54)
= 780 + 54.780 + .... + 516.780
= 780(1 + 54 + ... + 516)
= 13.60.(1 + 54 + ... + 516) ⋮ 13
Vậy C ⋮ 13.
Câu 4: Cho x + y = 12 và xy = 32. Tính x4 + y4.
Lời giải:
x + y = 12
⇔ (x + y)2 = 144
⇔ x2 + 2xy + y2 = 144
⇔ x2 + y2 = 144 – 2xy
⇔ x2 + y2 = 144 – 2.32 = 80
Bình phương 2 vế:
(x2 + y2)2 = 802
⇔ x4 + y4 + 2x2y2 = 6400
⇔ x4 + y4 = 6400 - 2(xy)2
⇔ x4 + y4 = 6400 – 2.322
⇔ x4 + y4 = 4352.
Vậy x4 + y4 = 4352.
Câu 5: Cho dãy số 1, 2, 3, 4, ..., 199, 200; hỏi dãy số có bao nhiêu số chẵn, bao nhiêu số lẻ?
Lời giải:
Tổng số hạng của dãy là:
(200 – 1) : 1 + 1 = 200 (số hạng)
Số lẻ bắt đầu từ 1 và kết thúc là 199, mỗi số lẻ cách nhau 2 đơn vị
Số các số lẻ là:
(199 – 1) : 2 + 1 = 100 (số lẻ)
Số các số chẵn là:
200 – 100 = 100 (số chẵn).
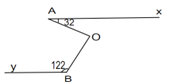
Câu 6: Cho hình vẽ biết : Ax // By, ^xAO=32°,^OBy=122° . Chứng tỏ OA vuông góc với OB.
Lời giải:
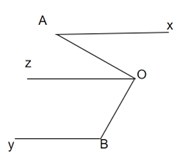
Theo giả thiết: Ax // By; ^xAO=32°,^OBy=122°
Kẻ tia Oz song song với Ax song song với By
⇒ ^OBy+^BOz=180° (vì là 2 góc trong cùng phía )
⇒ ^BOz=180°−^OBy=180°−122°=58°
Mà ta có Ax // Oz
⇒ ^AOz=^xAO=32° (vì là 2 góc so le trong bằng nhau )
⇒ ^AOB=^AOz+^BOz=32°+58°=90°
⇒ ^AOB là góc vuông
⇒ OA vuông góc với OB.
Câu 7: Hình thang ABCD (AB//CD) có AB = 4cm; MN = 6cm với M và N lần lượt là trung điểm của BC và AD. Khi đó độ dài cạnh CD là?
Lời giải:
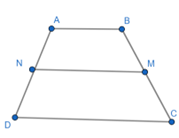
M, N lần lượt là trung điểm của BC và AD nên MN là đường trung bình của hình thang ABCD
⇒ MN = (AB + CD) : 2
⇒ CD = 2MN - AB = 2.6 - 4 = 8 (cm).
Câu 8: Biết Ax là tia phân giác của ^mAn và ^mAn=80° . Tính ^mAx .
Lời giải:
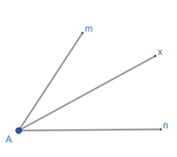
Do Ax là phân giác ^mAn nên ^mAx=^nAx=12^mAn=12.80°=40°
Vậy ^mAx=40° .
Câu 9: Cho ¯abc+¯acb=¯bca . Tìm phép cộng đã cho?
Lời giải:
Xét từng hàng, ta có:
Hàng đơn vị và hàng chục: b + c + 1 = 10 + c
⇒ b = 9
Hàng trăm: a + a + 1 = 9
⇒ a + a = 9 – 1 = 8
⇒ a = 4
Hàng đơn vị: c + 9 = 4 (loại vì không có số tự nhiên + 9 = 4)
⇒ c + 9 = 14
⇒ c = 14 − 9
⇒ c = 5
Vậy phép cộng trên là: 495 + 459 = 954.
Câu 10: Cho các số dương x, y, z thỏa mãn x + 2y + 3z ≥ 20. Tìm GTNN của A=x+y+z+3x+92y+4z .
Lời giải:
A=x+y+z+3x+92y+4z
A=14x+12y+34z+(34x+3x)+(12y+92y)+(4z+14z)
Áp dụng bất đẳng thức Cô-si cho 2 số dương: A=14x+12y+34z+(34x+3x)+(12y+92y)+(4z+14z)
A≥14(x+2y+3z)+2√34x.3x+2√12y.92y+2√4z.14z
A≥14.20++3+3+2=13
Vậy GTNN của A là 13 khi {34x=3x12y=92y4z=14zx+2y+3z=20⇔ {x=2y=3z=4 .
Câu 11: Số nhà của Alice là một số có 4 chữ số chia hết cho 5. Khi cô ấy di chuyển chữ số đầu tiên đến vị trí hàng đơn vị thì nhận thấy rằng số mới có 4 chữ số lớn hơn số nhà của cô ấy là 4707. Hỏi số nhà của Alice là bao nhiêu?
Lời giải:
Gọi số nhà của Alice là ¯abcd
Vì ¯abcd chia hết cho 5 nên d = 0 hoặc d = 5.
* Nếu d = 0 thì số nhà Alice có dạng ¯abc0
Ta có: ¯bc0a−¯abc0=4707
Ta thấy: a – 0 = 7 (hàng đơn vị) nên a = 7.
Suy ra có: ¯bc07−¯7bc0=4707
⇔ ¯bc07=¯7bc0+4707
Giả sử số nhỏ nhất của là 7000 thì 7000 + 4707 = 11707 là số có 5 chữ số. Nên loại.
* Nếu d = 5 thì số nhà Alice có dạng ¯abc5
Ta có: ¯bc5a−¯abc5=4707
Xét hàng đơn vị: a – 5 = 7, vì a có 1 chữ số nên a = 2
Xét hàng chục: 5 – c = 0 (nhớ thêm 1 từ hàng đơn vị) nên c = 4
Khi đó: ¯b452−¯2b45=4707(*)
Xét chữ số b có: 4 – b = 7 (nên b = 7)
Thay vào (*): 7452 – 2745 = 4707 (đúng, thỏa mãn)
Vậy số nhà Alice là 2745.
Câu 12: Giải phương trình: (2sinx – 1)(2sin2x + 1) = 3 – 4cos2x.
Lời giải:
(2sinx – 1)(2sin2x + 1) = 3 – 4cos2x
⇔ (2sinx – 1)(2sin2x + 1) = 3 – 4(1 - sin2x)
⇔ (2sinx – 1)(2sin2x + 1) = 3 – 4 + 4sin2x
⇔ (2sinx – 1)(2sin2x + 1) = 4sin2x – 1
⇔ (2sinx – 1)(2sin2x + 1) = (2sinx – 1)(2sinx + 1)
⇔ (2sinx – 1)(2sin2x + 1 – 2sinx - 1) = 0
⇔ 2.(2sinx – 1)(sin2x – sinx) = 0
⇔ 2.(2sinx – 1)(2sinxcosx – sinx) = 0
⇔ 2.(2sinx – 1).sinx(2cosx – 1) = 0
⇔ [sinx=12sinx=0cosx=12
⇔ [x=π6+k2πx=5π6+k2πx=kπx=π3+k2πx=2π3+k2π (k∈ℤ) .
Câu 13: Một lớp học có 28 nam và 24 nữ. Có bao nhiêu cách chia đều số học sinh vào các tổ với số tổ nhiều hơn sao cho số nam trong các tổ bằng nhau và số nữ trong các tổ bằng nhau? Cách chia nào để mỗi tổ có ít học sinh nhất?
Lời giải:
Vì số nam và số nữ chia đều vào các tổ nên 24 ⋮ x, 28 ⋮ x
Hay x thuộc ƯC(24;28)
Có ƯCLN(24;28) = 22 = 4.
Nên x ∈ Ư(4) = {1;2;4}
Có 2 cách để chia đều số học sinh là chia thành 2 tổ và 4 tổ
Nếu chia thành 2 tổ thì mỗi tổ sẽ có: 28 : 2 = 14 nam và 24 : 2 = 12 nữ
Nếu chia thành 4 tổ thì mỗi tổ sẽ có: 28 : 4 = 7 nam và 24 : 4 = 6 nữ
Vậy chia thành 4 tổ thì mỗi tổ sẽ có ít học sinh nhất.
Câu 14: Cho đoạn thẳng AB và hai tia Ax, By vuông góc với AB ở trên cùng một nửa mặt phẳng bờ AB. Gọi O là trung điểm của AB. Xét góc vuông ^mOn quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D. Chứng minh rằng:
a) CD luôn tiếp xúc với nửa đường tròn (O;AB2) .
b) AC.BD=AB24 .
Lời giải:
Xét góc vuông ^mOn quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D nên ^COD=90°
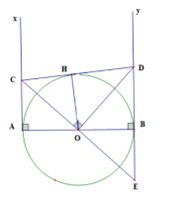
a) Kẻ OH ⊥ CD
Ta có DC = DE (chứng minh câu a)
Suy ra tam giác DCE cân ở D
Mà DO là đường cao nên DO đồng thời là phân giác của ^CDE
Suy ra ^CDE=^CDO
Xét ∆HOD và ∆BOD có
^DHO=^DBO=90°
OD là cạnh chung
ˆH=^ODB
Suy ra ∆HOD = ∆BOD (cạnh huyền – góc nhọn)
Do đó OH = OB, HD = BD (các cặp cạnh tương ứng)
Mà OB là bán kính của (O)
Suy ra H thuộc (O)
Lại có OH ⊥ CD nên CD là tiếp tuyến của (O)
c) Xét ∆HOC và ∆AOC có
OH = OA (= OB)
^CHO=^CAO=90°
OC là cạnh chung
Suy ra ∆HOC = ∆AOC (cạnh huyền – cạnh góc vuông)
Do đó HC = AC
Xét tam giác COD vuông tại O có OH ⊥ CD
Theo hệ thức lượng trong tam giác có
OH2 = CH . DH
Ta có: AC.BD=CH.DH=OH2=OA2=(BC2)2=BC24
Vậy AC.BD=AB24 .
Câu 15: Cho các số dương a, b, c thỏa mãn abc = 1.
Chứng minh a3(1+b)(1+c)+b3(1+c)(1+a)+c3(1+a)(1+c)≥34 .
Lời giải:
Áp dụng bất đẳng thức AM-GM ta có: a3(1+b)(1+c)+b+18+c+18≥33√a3(1+b)(1+c).b+18.c+18=3a4
Tương tự: b3(1+c)(1+a)+c+18+a+18≥33√b3(1+c)(1+a).c+18.a+18=3b4
c3(1+a)(1+c)+c+18+a+18≥33√c3(1+a)(1+c).c+18.a+18=3c4
Suy ra: a3(1+b)(1+c)+b3(1+c)(1+a)+c3(1+a)(1+c)≥34(a+b+c)
a3(1+b)(1+c)+b3(1+c)(1+a)+c3(1+a)(1+c)≥343√abc=34(BĐT Cô-si)
Vậy a3(1+b)(1+c)+b3(1+c)(1+a)+c3(1+a)(1+c)≥34
Dấu “=” xảy ra khi a = b = c = 1.
Câu 16: Nêu khái niệm của khối đa diện? Khối đa diện cần biểu diễn bao nhiêu hình chiếu. Nếu mặt đáy của hình lăng trụ đáy tam giác đều song song với mặt phẳng hình chiếu cạnh thì hình chiếu cạnh là hình gì?
Lời giải:
Khái niệm khối đa diện:
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện và kể cả hình đa diện đó.
* Khối đa diện cần biểu diễn: 3 hình chiếu (hình chiếu đứng, hình chiếu bằng, hình chiếu cạnh)
* Nếu mặt đáy của hình lăng trụ đáy tam giác đều song song với mặt phẳng hình chiếu cạnh thì hình chiếu cạnh là hình chữ nhật.
Câu 17: Tìm x biết (x + 2)(x + 2) – (x – 2)(x – 2) = 8x.
Lời giải:
(x + 2)(x + 2) – (x – 2)(x – 2) = 8x
⇔ (x + 2)2 – (x – 2)2 = 8x
⇔ (x + 2 + x – 2)(x + 2 – x + 2) = 8x
⇔ 2x.4 = 8x
⇔ 8x = 8x (luôn đúng)
Vậy phương trình có vô số nghiệm
Câu 18: Phân tích đa thức thành nhân tử x4 – 2x3 + 2x – 1.
Lời giải:
x4 – 2x3 + 2x – 1
= x4 – x3 – x3 + x2 – x2 + x + x – 1
= x3(x – 1) – x2(x – 1) – x(x – 1) + (x – 1)
= (x – 1)(x3 – x2 – x + 1)
= (x – 1)[x2(x – 1) – (x – 1)]
= (x – 1)(x – 1)(x2 – 1)
= (x – 1)3(x + 1).
Câu 19: Cho 1a+1b+1c=1a+b+c . Chứng minh 1an+1bn+1cn=1an+bn+cn (n là số lẻ).
Lời giải: 1a+1b+1c=1a+b+c
⇔ bc+ac+ababc=1a+b+c
⇔ (ab + bc + ca)(a + b + c) = abc
⇔ (ab + bc + ca)(a + b) + (abc + bcc + cca - abc) = 0
⇔ (ab + bc + ca)(a + b) +c2(a + b) = 0
⇔ (a + b)(a + c)(b + c) = 0
⇔ [a+b=0b+c=0c+a=0
Suy ra: trong a, b, c có 2 số đối nhau
Giả sử a, b đối nhau khi đó vì n lẻ nên 1an+1(−a)n+1cn=1an+(−a)n+cn (đúng)
Vậy 1an+1bn+1cn=1an+bn+cn .
Câu 20: Tìm số tập con của tập hợp A = {1; 2; 3}.
Lời giải:
Các tập con của A là: ∅; {1}; {2};{3}; {1; 2}; {1; 3}; {2; 3}; {1; 2; 3}.
Vậy tập hợp A có 8 tập hợp con.
Câu 21: Gọi S = 1 + 11 + 111 +… + 111….1. Tính S?
Lời giải:
S=1+11+111+...+111....1⏟n so 1
9S=9+99+999+...+999....9⏟n so 9
Áp dụng công thức tính tổng cấp số nhân Sn=u1.(1−qn)1−q
Khi đó: 9S=9+99+999+...+999....9⏟n so 9=10.(10n−19)−n
⇔ S=19[10.(10n−19)−n] .
Câu 22: Cho tam giác ABC cân tại A. ˆA=20° . Trên AB lấy điểm D sao cho AD = BC.Tính góc ^BDC,^ACD .
Lời giải:
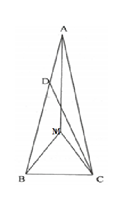
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
⇒ BM = CM
⇒ M thuộc trung trực của BC
Lại có: AB = AC(ABC cân tại A)
⇒ A thuộc trung trực của BC
Do đó: AM là trung trực của BC
⇒ AM là phân giác góc ^BAC
⇒ ^MAB=^MAC=12^BAC=12.20°=10°
Vì tam giác ABC cân tại A nên: ^CBA=^BCA=180°−20°2=80°
Lại có: ^MCA=^ACB−^MCB=80°−60°=20° (tam giác BMC đều)
Suy ra: ^CMA=180°−10°−20°=150°
Xét tam giác CMA và tam giác ADC có:
AC chung
^MCA=^DAC=20°
CM = DA (=BC)
⇒ ∆CMA = ∆ADC (c.g.c)
⇒ ^CDA=^CMA=150°;^ACD=^MAC=10°
Mặt khác: ^CDA+^BDC=180° (2 góc kề bù)
Suy ra: ^BDC=180°−^CDA=180°−150°=30°
Vậy ^BDC=30°;^ACD=10° .
Câu 23: Cho tập A= (m; m + 2) và tập B = (0; 5). Có bao nhiêu số nguyên m để A giao B khác rỗng?
Lời giải:
A∩B = ∅ ⇔ [m+2≤0m≥5⇔[m≤−2m≥5
Vậy A∩B ≠ ∅ khi -2 < m < 5.
Vậy m ∈ [-1;4]
Có: 4 – (-1) + 1 = 6 số nguyên m.
Câu 24: Cho hình chữ nhật ABCD. Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AB, AD theo thứ tự tại E, F. Tia phân giác của góc AFE cắt AC tại H. Gọi K là hình chiếu của A trên FH.
a) Biết AB = 4cm, AC = 6cm. Tính AE, DE.
b) Chứng minh AB.AE = AD.AF.
Lời giải:
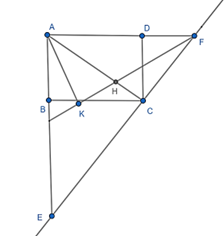
a) CB2 = AB2 + AC2 = 42 + 62 = 52
Suy ra: CB=√52 (cm)
Xét tam giác vuông ACE (vì CE vuông góc AC) có CB vuông góc AE
Nên: CA2 = AB.AE
⇒ AE=CA2AB=624=9 (cm)
DE2 = AE2 + AD2 = 92 + BC2 = 92 + 52 = 1333
⇒ DE=√133 cm
b) Xét tam giác BAC và tam giác AEC có:
Chung ˆA
^ABC=^ACE=90°
⇒ ∆ABC ∽ ∆ACE (g.g)
⇒ ABAC=ACAE⇒ AC2 = AB.AE (1)
Xét tam giác vuông ACF tại C có DC là đường cao, có:
AD.AF = AC2 (2)
Từ (1) và (2): AB.AE = AD.AF
Câu 25: Tìm nghiệm âm lớn nhất của phương trình tan5x.tanx = 1.
Lời giải:
tan5x.tanx = 1
⇔ tan5x=1tanx
⇔ tan5x = cotx = tan(π2−x)
⇔ 5x=π2−x+kπ
⇔ x=π12+kπ6 (k∈ℤ) .
Nghiệm âm lớn nhất khi k = -1
Vậy x=π12−π6=−π12 .
Câu 26: Cho hàm số y = ax + 3. Hãy xác định hệ số a trong trường hợp sau:
Đồ thị của hàm số song song với đường thẳng y = -2x.
Lời giải:
Theo đề bài ta có b ≠ b' (vì 3 ≠ 0)
Vậy đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi a = a' tức là: a = -2.
Hàm số có dạng y = 2x + 3.
Câu 27: Cho (O; R) đường kính AB và M nằm trên (O; R) với MA < MB (M khác A và B). Tiếp tuyến tại M của (O; R) cắt tiếp tuyến tại A và B của (O; R) theo thứ tự ở C và D.
a) Chứng minh ACDB là hình thang vuông
b) AD cắt (O; R) tại E, OD cắt MB tại N. Chứng minh OD vuông góc MB và DE.DA = DN.DO
c) Cho AM = R. Tính theo R diện tích ACDB.
Lời giải:
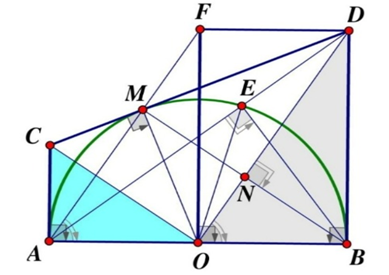
a) AC ⊥ AB vì AC là tiếp tuyến
BD ⊥ AB vì BD là tiếp tuyến
Suy ra: AC // DB ⇒ ACDB là hình thang
Lại có: ^BAC=^DBA=90° nên ACDB là hình thang vuông
b) Theo tính chất 2 tiếp tuyến cắt nhau
Ta có: MD = MB
OM = OB = R
Nên OD là đường trung trực của MB
⇒ OD ⊥ MB và MN = NB
Xét tam giác OBD vuông tại B có OD ⊥ BN
Áp dụng hệ thức lượng trong tam giác vuông: DN.DO = BD2 (1)
Tam giác AEB có OE = OA = OB = R nên tam giác AEB vuông tại E
Suy ra: BE ⊥ DA
Lại có: tam giác ABD vuông tại B và OD ⊥ BE
⇒ DE.DA = BD2 (2)
Từ (1) và (2) suy ra: DE.DA = DN.DO
c) Ta có: MA = OA = OM = R nên tam giác AMO đều
⇒ ^AOM=60°⇒^AOC=30°(vì OC là phân giác)
⇒ ^BOM=120°⇒^BOD=60°
Xét trong tam giác BOD có: BD=OB.tan60°=R√3
Trong tam giác OCA có: AC=OA.tan30°=R√33
Vì ACDB là hình thang vuông AB là đường cao
Nên SACDB=12.AB.(AC+BD)=4R2√33 .
Câu 28: Cho y = ax – 3.
a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm có hoành độ là 2.
b) Đồ thị hàm số cắt đường thẳng y = -3x + 2 tại điểm có tung độ là 3.
Lời giải:
a) Vì đường thẳng y = 2x - 1 cắt đồ thị trên tại điểm có hoành độ bằng 2
⇒ x = 2
Thay x = 2 vào đường thẳng y = 2x - 1
⇒ y = 2.2 – 1 = 3
Vậy y = 3.
Thay x = 2; y = 3 vào đồ thị trên:
⇒ 3= a.2 − 3
⇒ a = 3
Vậy a = 3 hay đồ thị y = 2x – 3.
b) Vì đường thẳng y = -3x + 2 cắt đồ thị trên tại điểm có tung độ bằng 3
⇒ y = 3
Thay y = 3 vào đường thẳng ta có: 3 = -3x + 2
⇒ x=−13
Thay x=−13 vào đồ thị y = ax – 3
Suy ra: 3=a(−13)−3 ⇒ a = –18
Vậy a = -18 hay đồ thị y = –18x – 3.
Câu 29: Chứng minh sin4a + cos4a = 34+14cos4a .
Lời giải:
sin4a + cos4a = (sin2x + cos2x)2 – 2sin2xcos2x = 1 – 2(sinxcosx)2
= 1−2(12sin2x)2
=1−12sin22x
=1−12(1−cos22x)
=12+cos22x
=34+14cos4a.
Câu 30: Cho tam giác ABC có b = 7; c = 5, cosA=35 . Tính đường cao ha của tam giác ABC?
Lời giải:
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.35 = 32
Nên a=4√2
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 1625
Mà sinA > 0 nên sinA = 45
SABC=12.b.c.sinA=12.a.ha
Suy ra: ha = bcsinAa=7.5.454√2=7√22 .
Câu 30: Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
a) Tính HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Lời giải:
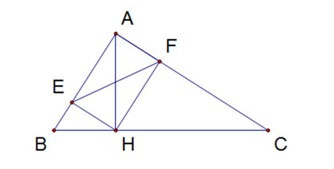
a) Xét ΔABH và ΔCBA có:
^ABC chung
^AHB=^BAC=90°
⇒ ΔABH ∽ ΔCBA(g.g)
⇒ ABBC=AHAC=35⇒ABBC=35
Hay 15BC=35⇒BC=25(cm)
Xét ΔABC vuông tại A, đường cao AH có:
AB2 = HB.BC ( hệ thức lượng trong Δ vuông )
⇔ 152 = HB.25
⇔ 225 = HB.25
⇔ HB = 9 (cm)
HB + HC = BC
⇔ 9 + HC = 25
⇔ HC = 16(cm)
b) Xét tứ giác AEHF có: ^EAF=^AEH=^AFH=90°
Nên AEHF là hình chữ nhật
⇒ AH = EF
Xét ΔABC vuông tại A, đường cao AH có:
AB.AC = AH.BC (hệ thức lượng trong Δ vuông)
⇒ AB.AC = EF.BC (vì AH = EF).
Câu 31: Cho tam giác đều ABC. Gọi M là điểm thuộc cạnh BC. Gọi E, F lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC. Gọi I là trung điểm của AM, D là trung điểm của BC.
a, Tính góc DIE và góc DIF.
b, Chứng minh rằng: tứ giác DEIF là hình thoi.
Lời giải:
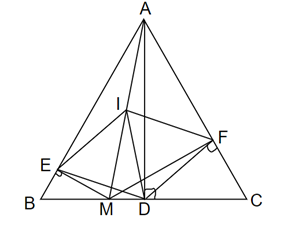
a) + ΔAME vuông tại E có đường trung tuyến EI
⇒ EI = 12 AM ⇒ EI = MI = AI
+ Tương tự ta có: DI = FI = AI = MI
Tam giác AEI cân tại I nên ^IAE=^IEA
⇒ ^EIM=2^IAE
Tương tự: ^MID=2^IAD
⇒ ^EIM+^MID=2^IAE+2^IAD
^DIE=2.30°=60°(do góc ^EAD=30°)
^DIF=180°−(^AIF+^MID)=180°−(180°−2^IAF+180°−2^IMC)
^DIF=180°−(360°−240°)(do ^IAF+^IMC=120° )
Suy ra: ^DIF=60°
b) Tam giác DIE có: DI = EI mà ^DIE=60° nên tam giác DIE đều
Suy ra: DI = EI = DE (1)
Tương tự: tam giác DIF đều vì DI = FI mà ^DIF=60°
Suy ra: DI = FI = DF (2)
Từ (1) và (2) ⇒ DE = EI = IF = DF
⇒ tứ giác DEIF là hình thoi.
Câu 32: Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Lời giải:
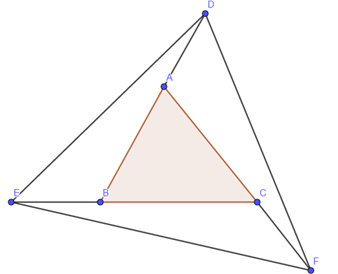
Xét tam giác EBD và tam giác FCE có:
EC = DB (vì AB = BC; AD = EB nên EB + BC = AB + AD)
^EBD=^FCE(cùng là 2 góc ngoài của 1 tam giác đều)
EB = FC (giả thiết)
Suy ra: ∆EBD = ∆FCE (c.g.c)
⇒ DE = EF (1)
Chứng minh tương tự: ∆EBD = ∆DAF (c.g.c)
⇒ DE = FD (2)
Từ (1) và (2): DE = DF = EF
Vậy tam giác DEF đều.
Câu 33: Tìm x sao cho: (x + 5)(4 − 3x) − (3x + 2)2 + (2x + 1)3 = (2x − 1)(4x2 + 2x + 1).
Lời giải:
(x + 5)(4 − 3x) − (3x + 2)2 + (2x + 1)3 = (2x − 1)(4x2 + 2x + 1)
⇔ −3x2 − 11x + 20 − 9x2 − 12x – 4 + 8x3 + 12x2 + 6x + 1 = 8x3 – 1
⇔ −17x + 18 = 0
⇔ x=1817 .
Câu 34: Phân tích số 90 ra thừa số nguyên tố.
Lời giải:
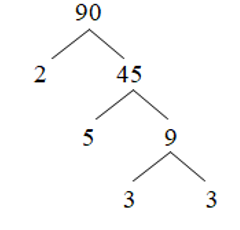
Nên 90 = 2.5.3.3 = 2.32.5.
Câu 35: Tìm các số tự nhiên n sao cho 6n + 16 chia hết cho n + 2.
Lời giải:
Ta có: 6n + 16 = 6(n + 2) + 4
Vì 6(n + 2) chia hết cho n + 2
Để 6n + 16 chia hết cho n + 2 thì 4 chia hết cho n + 2
Hay n + 2 ∈ Ư(6)
⇒ n + 2 ∈{1; 2; 3; 6}
⇒ n ∈ {-1;0;1;4}
Vì n là số tự nhiên nên n ∈ {0; 1; 4}.
Vậy n ∈ {0; 1; 4}.
Câu 36: Tính cos4a theo cosa.
Lời giải:
cos4a = cos(2.2a) = 2cos22a – 1
Mà cos2a = 2cos2a – 1
Suy ra: cos4a = 2cos22a – 1 = 2(2cos2a – 1)2 – 1 = 8cos4a – 8cos2a + 1.
Câu 37: Tìm ab thỏa mãn điều kiện 47<ab<23 và 7a + 4b = 1994.
Lời giải:
Ta có: 7a + 4b = 1994 nên 7a = 1994 – 4b
⇒ a=1994−4b7=19947−47b
Thay a=1994−4b7=19947−47b vào điều kiện 47<ab<23 ta được: 47<19947−47bb<23⇔47<19947b−47<23⇔87<19947b<2621⇔8<1994b<263
Suy ra: {8<1994b1994b<263⇔{8b<99426b>5982⇔{b<24914b>230113
⇒ 230113<b<24914
Suy ra: 231 < b < 249
Vậy b = 243
Suy ra: a=1994−4.2437=146
Vậy phân số cần tìm là ab=146243 .
Câu 38: Tìm x, y thỏa mãn 2015(x2 + y2) – 2014(2xy + 1) = 25.
Lời giải:
2015(x2 + y2) – 2014(2xy + 1) = 25
⇔ x2 + y2 + 2014(x – y)2 = 2039
Nếu |x−y|≥2 thì (x−y)2≥4
Suy ra: Vế trái > 8056 > 2039 (loại)
⇒ |x−y|≤1
⇒ [|x−y|=0|x−y|=1
Nếu x = y thì 2x2 = 2039 (vô lý)
Nếu y = x – 1 thì ta có: 2x2 – 2x + 1 = 25
⇔ x2 – x – 12 = 0
⇔ [x=4x=−3
Suy ra: [y=3y=−4
Nếu y = x + 1 thì: x2 + (x + 1)2 + 2014(x – x – 1)2 = 2039
⇔ 2x2 + 2x + 1 + 2014 – 2039 = 0
⇔ 2x2 + 2x – 24 = 0
⇔ x2 + x – 12 = 0
⇔ [x=3x=−4
Suy ra: [y=4y=−3
Vậy (x,y) ∈ {(4;3), (-3;-4), (3;4), (-4;-3)}.
Câu 39: Bác Hùng và bác Long cùng làm chung một công việc, sau 2 giờ thì hoàn thành. Nếu bác Hùng làm 1 mình thì sau 5 giờ mới hoàn thành. Hỏi nếu bác Long làm một mình thì sau bao nhiêu lâu sẽ hoàn thành công việc đó?
Lời giải:
1 giờ cả 2 bác làm được: 1:2=12 (công việc)
1 giờ bác Hùng làm được: 1:5=15 (công việc)
1 giờ bác Long làm được: 12−15=310 (công việc)
Một mình bác Long làm trong: 1:310=103 (giờ) = 3 giờ 20 phút.
Câu 40: Lớp 5A có số học sinh nữ bằng số học sinh của lớp. Nếu lớp 5A bớt đi 2 bạn nữ thì số học sinh nữ bằng số học sinh cả lớp. Tìm số học sinh ở lớp 5A.
Lời giải:
2 học sinh nữ ứng với: (học sinh).
Số học sinh của lớp 5A là: (học sinh).
Câu 41: Tìm x biết 9x – 1 = 9.
Lời giải:
9x – 1 = 9
⇔ 9x – 1 = 91
⇔ x – 1 = 1
⇔ x = 2
Vậy x = 2.
Câu 42: Cho tam giác ABC. Chứng minh cotA.cotB + cotB.cotC + cotC.cotA = 1.
Lời giải:
Ta có:
cotA = -cot(π – A) = -cot(B + C)
Suy ra: cotA(cotC + cotB) = 1 – cotB.cotC
Xét cotA.cotB + cotB.cotC + cotC.cotA
= cotA(cotB + cotC) + cotB.cotC
= 1 – cotB.cotC + cotB.cotC
= 1.
Vậy cotA.cotB + cotB.cotC + cotC.cotA = 1.
Câu 43: Tìm 6 chữ số khác nhau a, b, c, d, e, g sao cho có giá trị nhỏ nhất.
Lời giải:
Ta thấy: a,b,c,d,e,g ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
có giá trị nhỏ nhất thì a – d = 1
(nhỏ nhất)
(lớn nhất)
khi đó:
Vậy b = 0, c = 1, e = 9, g = 8
a và b là một trong các cặp số sau: 3 và 2, 4 và 3, 5 và 4, 6 và 5, 7 và 6.
Câu 44: Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin A
Lời giải:
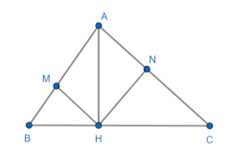
Áp dụng hệ thức lượng trong tam giác vuông AHB, AHC có:
AH2 = AM.AB
AH2 = AN.AC
Suy ra: AM.AB = AN. AC
⇒
Xét tam giác AMN và tam giác ABC có:
chung
⇒ ∆AMN ∽ ∆ABC (c.g.c)
⇒
⇒ (1)
Lại có:
Suy ra: (2)
Thay (2) vào (1) có: .
Câu 45: Tìm x biết 18 chia hết cho x và x > 3.
Lời giải:
Vì 18 chia hết cho x nên x ∈ Ư(18)
Mà x > 3 nên ta chọn các ước dương của 18
Các ước dương của 18 là: Ư(18) ∈ {1; 2; 3; 6; 9; 18}
Vậy x ∈ {6; 9; 18}.
Câu 46: Số nghiệm của phương trình với π ≤ x ≤ 5π?
Lời giải:
⇔
⇔
Vì π ≤ x ≤ 5π nên
⇔
⇔
Vì k ∈ ℤ nên k = 1 hoặc k = 2.
Vậy phương trình có hai nghiệm nằm trong đoạn [π; 5π].
Câu 47: Với x > 9. Tìm GTNN của biểu thức .
Lời giải:
Áp dụng bất đẳng thức Cô-si cho 2 số dương ta có:
Vậy GTNN của P là 12 khi (do ) ⇔ x = 36.
Câu 48: Một cột đèn có bóng trên mặt đất dài 8,5m . Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 38°. Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân).
Lời giải:
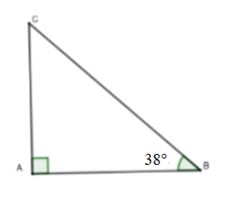
Gọi chiều cao cột đèn là AC, AB là bóng của cột đèn trên mặt đất, AB = 8,5 m.
Góc tạo bởi tia nắng mặt trời với mặt đất là
Xét tam giác ABC vuông tại A, ta có:
AC = AB . tanB = 8,5 . tan38° ≈ 6,6 (m).
Vậy cột đèn cao khoảng 6,6 m.
Câu 49: Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.
Lời giải:
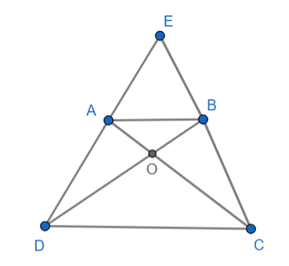
Xét ∆ADC và ∆BCD, ta có:
AD = BC (tính chất hình thang cân)
(gt)
DC chung
Do đó: ∆ADC = ∆BCD (c.g.c) ⇒
Trong ∆OCD ta có:
⇒ ∆OCD cân tại O
⇒ OC = OD (1)
AC = BD (tính chất hình thang cân)
⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
Vậy OA = OB; OC = OD.
b) Theo phần a có: OA = OB
∆ADC = ∆BCD (c.g.c)
⇒ ∆EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.
Câu 50: Cho cosα = 0,2 với π < a < 2π. Tính .
Lời giải:
Do π < a < 2π nên . Suy ra:
Ta có:
Suy ra:
Câu 51: Cho mảnh vườn hình chữ nhật có độ dài hai cạnh là 6m và 10m. Người ta trồng 4 bồn cỏ có dạng hình tam giác xung quanh như hình vẽ, phần còn lại trồng hoa.
a) Tính diện tích phần đất dùng để trồng cỏ.
b) Mỗi mét vuông trồng cỏ chi phí mua hạt giống hết 25000 đồng, công trồng hết 30000 đồng. Mỗi mét vuông trồng hoa chi phí mua hoa giống hết 80000 đồng, công trồng hết 35000 đồng. Hỏi tổng chi phí làm mảnh vườn hết bao nhiêu tiền?
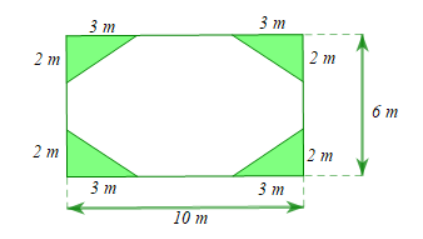
Lời giải:
a) Diện tích một bồn cỏ hình tam giác là:
Diện tích bốn bồn cỏ hình tam giác là: 4.3 = 12 (m2)
b) Diện tích mảnh vườn hình chữ nhật là: 10.6 = 60 (m2)
Diện tích trồng hoa là: 60 – 12 = 48 (m2)
Chi phí làm mảnh vườn đó là:
(25000 + 30000).12 + (80000 + 35000).48 = 6180000 (đồng).
Câu 52: Trong một mảnh vườn hình vuông có kích thước cạnh là 7m (như hình vẽ). Có ba bản vẽ đã được về với yêu cầu phần diện tích đất còn lại (phần màu xám trên bản vê) của vườn là lớn nhất. Bản vẽ nào dùng được? Vì sao?
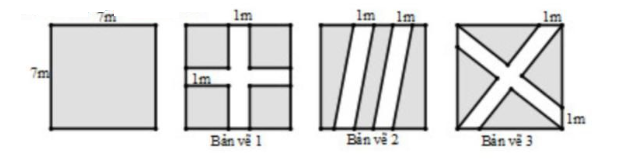
Lời giải:
Xét bản vẽ 1: diện tích phần màu trắng là:
2.1.7 – 1.1 = 12 (m2)
Diện tích phần màu xám là:
7.7 – 12 = 37 (m2)
Xét bản vẽ 2: (2 hình màu trắng là hình bình hành có đáy là 1m, đường cao 7m)
Diện tích phần màu xám là:
7.7 – 2.7.1 = 35 (m2)
Xét bản vẽ 3:
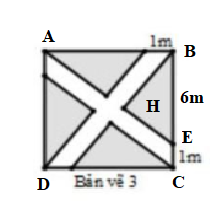
Ta có: (m)
(m)
Tam giác BHE vuông tại H nên (m)
Diện tích phần màu xám là:
Suy ra: Chọn bản vẽ 1 để diện tích phần màu xám là lớn nhất.
Câu 53: Một số học sinh dự thi học sinh giỏi toán. Nếu xếp 25 học sinh vào một phòng thì còn thừa 5 học sinh chưa có chỗ. Nếu xếp 28 học sinh vào một phòng thì thừa 1 phòng. Tìm số học sinh dự thi?
Lời giải:
Nếu xếp 28 học sinh vào một phòng thì thừa 1 phòng
Số học sinh chênh lệch trong 2 trường hợp xếp phòng là:
5 + 28 = 33 (học sinh)
Số học sinh chênh lệch ở mỗi phòng trong 2 trường hợp là:
28 – 25 = 3 (học sinh)
Số phòng thi là:
33 : 3 = 11 (phòng)
Số học sinh dự thi là:
25.11 + 5 = 280 (học sinh).
Câu 54: Cho tam giác ABC nhọn, vẽ AH vuông góc BC tại H. Chứng minh AC2 + BH2 = AB2 + CH2.
Lời giải:
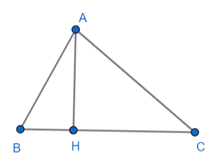
Tam giác ABH vuông tại H nên AB2 = AH2 + BH2
Tam giác ACH vuông tại H nên AC2 = AH2 + CH2
Lại có: AC2 + BH2 = AH2 + CH2 + BH2 = (AH2 + BH2) + CH2 = AB2 + CH2.
Câu 55: Cho 3 đường thẳng (d1): ; (d2): y = -2x – 4; (d3): .
a) Vẽ đồ thị các hàm số trên cùng một trục tọa độ. Nhận xét vị trí của 3 đường thẳng trên.
b) Cho (d2) cắt (d1) và (d3) tại 2 điểm A và B; (d1) cắt trục Ox tại C. Tính diện tích tam giác ABC.
Lời giải:
a) Ta thấy: Hệ số góc của d1 và d3 bằng nhau và – 1 khác - 4
Nên d1 // d3
Xét vị trí tương đối của d2 với d3 thấy: nên d2 cắt d3
Tương tự: d1 cắt d2.
b)
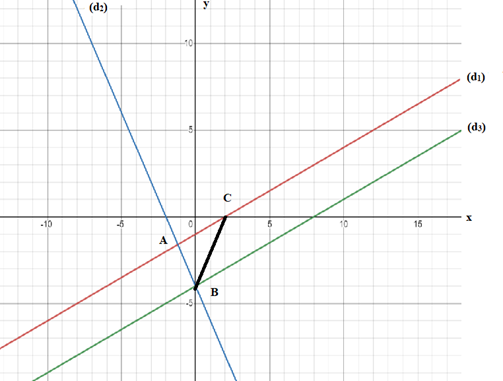
Ta thấy: (d2) ⊥ (d1), ⊥ (d3) vì:
Xét phương trình hoành độ giao điểm (d2) và (d1):
⇔
Suy ra:
Xét phương trình hoành độ giao điểm (d2) và (d3):
⇔
Suy ra: B(0;-4)
Có: C thuộc Ox nên yC = 0
Lại có C thuộc d1 nên:
Suy ra: C(2;0)
SABC = .
Câu 56: Cho 3 số dương x, y, z có tích bằng 144. Tìm GTNN của biểu thức
Lời giải:
Áp dụng bất đẳng thức Cosi, ta có:
Dấu “=” xảy ra khi:
Vậy GTNN của P là 32 khi (x; y; z) = (1; 4; 36).
Câu 57: Tìm x sao cho 24 chia hết cho x, 30 chia hết cho x, 48 chia hết cho x và x lớn nhất.
Lời giải:
Vì 24 ⋮ x, 30 ⋮ x, 48 ⋮ x và x lớn nhất
Nên x = ƯCLN(24, 30, 48)
Ta có:
24 = 23.3
30 = 2.3.5
48 = 24.3
Suy ra: ƯCLN(24, 30, 48) = 2.3 = 6
Vì x lớn nhất nên x = 6.
Vậy x = 6.
Câu 58: Kim giờ và kim phút chỉ thời gian lúc 12 giờ. Người ta để ý rằng cứ cách 1 giờ thì hai kim vuông góc với nhau hai lần. Hỏi thời gian để hai kim vuông góc với nhau lần đầu tiên gần với số nào sau đây?
A. 15 phút
B. 16 phút
C. 17 phút
D. 18 phút
Lời giải:
Chọn B
Vì cứ 15 phút thì kim giờ lại nhích 1 vạch.
Vì kim giờ nhích 1 vạch thì kim phút cũng nhích một vạch nên thời gian để hai kim vuông góc với nhau lần đầu tiên là: 15 + 1 = 16 (phút).
Câu 59: Cho hai tập hợp A = {1; 2; 3} và B ={1; 2; 3; 4; 5}. Có tất cả bao nhiêu tập X thỏa mãn A ⊂ X ⊂ B?
Lời giải:
Ta có: A ⊂ X nên X có ít nhất 3 phần tử {1; 2; 3}.
Ta có: X ⊂ B nên X phải có nhiều nhất 5 phần tử và các phần tử thuộc X cũng thuộc B
Do đó các tập X thỏa mãn là: {1; 2; 3}, {1; 2; 3; 4}, {1; 2; 3; 5}, {1; 2; 3; 4; 5}.
Vậy có 4 tập X thỏa mãn.
Câu 60: Tìm giá trị lớn nhất của M = sin6x – cos6x.
Lời giải:
Ta có:
M = sin6x – cos6x
M = (sin2x – cos2x)(sin4x + sin2xcos2x + cos4x)
= – cos2x(1 - sin2xcos2x)
(do cos2x ≤ 1)
Vậy GTLN của M bằng 1 khi cos2x = 1 ⇔ 2x = k2π ⇔ x = kπ (k ∈ ℤ).
Câu 61: Cho tam giác ABC, D thuộc BC. Qua D kẻ các đường thẳng song song với AC và AB cắt AB, AC lần lượt tại E, F. Chứng minh rằng .
Lời giải:
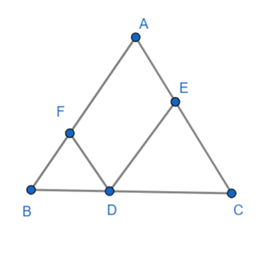
Áp dụng định lý Ta-lét:
DE // AC nên:
DF // AB nên:
Cộng (1) và (2) ta được:
Vậy .
Câu 62: So sánh 2300 và 3200.
Lời giải:
2300 = (23)100 = 8100
3200 = (32)100 = 9100
Vì 8100 < 9100 nên 2300 < 3200.
Câu 63: Cho tam giác ABC, trực tâm H là trung điểm của đường cao AD. Chứng minh rằng: tanB.tanC = 2.
Lời giải:
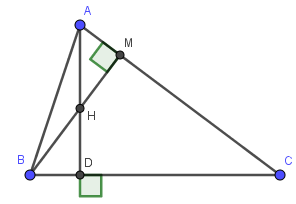
Gọi M là giao điểm BH và AC
Do H là trực tâm nên AM ⊥ AC
Ta có:
Xét tam giác BHD và tam giác ACD có:
Suy ra: ∆BHD ∽ ∆ACD (g.g)
⇒
⇔ (do H là trung điểm AH nên 2HD = AD)
⇔
Xét trong tam giác vuông ABD có: tanB =
Trong tam giác vuông ADC có: tanC =
Suy ra: tanB.tanC = 2.
Câu 64: Cho tam giác đều ABC cạnh a, M là trung điểm BC. Tính độ dài .
Lời giải:
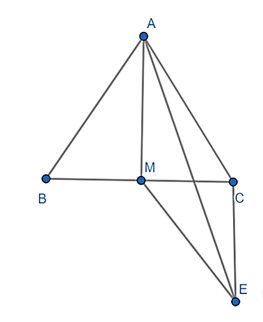
(hình vẽ)
Suy ra:
Vậy: .
Câu 65: Tính tổng 12 + 22 + … + n2.
Lời giải:
F = 12 + 22 + 32 + … + n2
F = 1 + (1 + 1).2 + (1 + 2).3 + (1 + 3).4 + … + (1 + n – 1)n
F = 1 + (2 + 1.2) + (3 + 2.3) + (4+ 3.4) + … + [n + (n – 1)n]
F = (1 + 2 + 3 + 4 + … + n) + [1.2 + 2.3 + 3.4 + …. + (n – 1)n]
Đặt A = 1 + 2 + 3 + 4 + … + n thì A =
Đặt B = [1.2 + 2.3 + 3.4 + …. + (n – 1)n]
Xét 3B = 1.2.3 + 2.3.3 + 3.4.3 + … + (n – 1).n.3
3B = [1.2.3 + 2.3.4 + … + (n – 1).n.(n + 1)] – (1.2.3 + 2.3.4 + … + (n – 2)(n – 1)n)
3B = (n – 1)n(n + 1)
B =
Từ (1) và (2) suy ra:
F =
Vậy F = 12 + 22 + 32 + … + n2 .
Câu 66: Cô giáo chủ nhiệm muốn chia 24 quyển vở, 48 bút bi và 36 gói bánh thành một số phần thưởng như nhau để trao trong dịp sơ kết hợc kì. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó mỗi phần thưởng có bao nhiêu quyển vở, bút bi và gói bánh?
Lời giải:
Gọi a là số phần thưởng để cô giáo chủ nhiệm trao trong dịp sơ kết học kì (a ∈ ℕ*; a < 24).
Để số phần thưởng là nhiều nhất thì a phải là số lớn nhất sao cho 24 chia hết cho a; 48 chia hết cho a; 36 chia hết cho a.
Tức là a = ƯCLN (24, 48, 36).
Ta có:
24 = 23.3
48 = 24.3
36 = 22.32
Suy ra: ƯCLN (24, 48, 36) = a = 22.3 = 12.
Vậy có thể chia được nhiều nhất 12 phần thưởng. Trong đó có 2 quyển vở, 4 bút bi và 3 gói bánh.
Câu 67: Tính: (−0,4)2 − (−0,4)3.(−3).
Lời giải:
(−0,4)2 − (−0,4)3.(−3) = .
Câu 68: Chứng minh rằng: 11n+2 + 122n+1 chia hết cho 133.
Lời giải:
11n+2 + 122n+1
= 121.11n + 12.144n
= (133 – 12).11n + 12.144n
= 133.11n + 12.(144n – 11n)
Ta thấy: 133.11n chia hết cho 133
144n – 11n chia hết cho (144 – 11) tức chia hết cho 133.
Vậy 133.11n + 12.(144n – 11n) chia hết cho 133 hay 11n+2 + 122n+1 chia hết cho 133.
Câu 69: Cho tập hợp X = {1;2;4;7}.Tập hợp nào là tập hợp con của tập hợp X?
A. {1; 7}
B. {1; 5}
C. {2; 5}
D. {3; 7}
Lời giải:
Vì 3 ∉ X và 5 ∉ X nên loại B, C, D
Vậy A là đáp án đúng.
Câu 70: Một sản phẩm được hạ giá 60%. Hỏi sản phẩm đó phải tăng giá lên bao nhiêu % để trở về giá ban đầu?
Lời giải:
Tỉ số % của giá bán sau khi giảm là:
100% - 60% = 40%
Tỉ số % giữa giá mới và giá bán lúc đầu là:
100 : 40 = 2,5 = 250%
Cần tăng giá mới của sản phẩm thêm số % để được giá ban đầu là:
250% - 100% = 150%.
Câu 71: Góc ngoài của một tam giác cân hơn góc trong kề với nó 90 độ. Tính các góc trong của tam giác đó?
Lời giải:
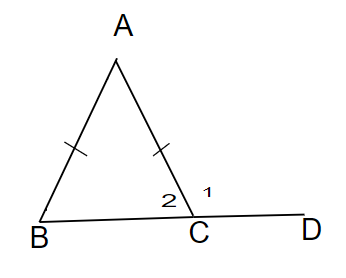
Do theo giả thiết: (*)
Mà: (định lý góc ngoài tam giác)
Vì tam giác BAC cân nên:
Khi đó (*) trở thành:
Mà ABC cân tại A nên: .
Câu 72: Cho p và p + 2 là các số nguyên tố (p > 3). Chứng minh rằng p + 1 ⋮ 6.
Lời giải:
Vì p là số nguyên tố và p > 3, nên số nguyên tố p có 1 trong 2 dạng: 3k + 1, 3k + 2
- Nếu p = 3k + 1 thì p + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) ⋮ 3
Suy ra: p + 2 là hợp số (trái với đề bài p + 2 là số nguyên tố).
- Nếu p = 3k + 2 thì p + 1 = 3k + 3 = 3(k + 1) ⋮ 3 (1)
Do p là số nguyên tố và p > 3 nên p lẻ ⇒ k lẻ ⇒ k + 1 chẵn ⇒ k + 1 ⋮ 2 (2)
Từ (1) và (2) ⇒ p + 1 ⋮ 6
Vậy p + 1 ⋮ 6.
Câu 73: Cho 2 đường thẳng d1 : y = -4x + m + 1, d2 : y = x + 15 - 3m.
a) Tìm m để d1 cắt d2 tại điểm C trên trục tung.
b) Với m vừa tìm được, hãy tìm giao điểm A, B của d1, d2 với Ox.
Lời giải:
a) Để d1 cắt d2 tại điểm C trên trục tung thì x = 0
Khi đó ta có: yC = -4.0 + m + 1 =
⇔ 4m = 14
⇔ m =
Suy ra:
b) Với m = ta có: d1:
d1 giao Ox tại A nên yA = 0, khi đó: ⇒
d2 giao Ox tại B nên yB= 0, khi đó: ⇒ .
Câu 74: Phân tích đa thức thành nhân tử: 16x2 – (x + 1)2.
Lời giải:
16x2 – (x + 1)2
= (4x)2 – (x + 1)2
= (4x + x + 1)(4x – x – 1)
= (5x + 1)(3x – 1)
Câu 75: Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM = 15, BN = 12 và tam giác CMN có diện tích là . Tính độ dài đoạn thẳng MN.
Lời giải:
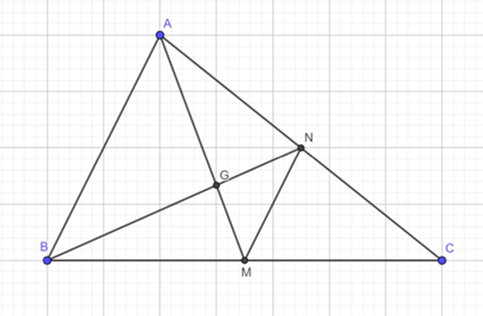
Suy ra: SABC = 4SCMN =
Lại có:
⇒
Hay:
Ta có: AB2 = AG2 + GB2 – 2.AG.GB.cos
⇒
M, N là trung điểm BC, AC nên MN là đường trung bình của tam giác ACB
Nên
Vậy .
Câu 76: Chọn khẳng định đúng:
A. Hai vectơ cùng hướng thì cùng phương.
B. Hai vectơ cùng phương thì cùng hướng.
C. Hai vectơ cùng phương thì có giá song song với nhau.
D. Hai vectơ cùng hướng thì có giá song song nhau.
Lời giải:
Đáp án: A
Giải thích các bước giải:
Hai vecto cùng phương nếu giá của chúng song song hoặc trùng nhau
Hai vecto cùng phương có thể cùng hoặc ngược hướng
A. Hai vectơ cùng hướng thì cùng phương.
⇒ Đúng vì để hai vectơ cùng hướng thì trước tiên chúng phải cùng phương
B. Hai vectơ cùng phương thì cùng hướng.
⇒ Sai, chúng có thể ngược hướng
C. Hai vectơ cùng phương thì có giá song song với nhau.
⇒ Sai, giá có thể trùng nhau
D. Hai vectơ cùng hướng thì có giá song song nhau.
⇒ Sai, giá có thể trùng nhau.
Câu 77: Tìm đa thức M, biết: M + (5x2 – 2xy) = 6x2 + 9xy – y2.
Lời giải:
M + (5x2 – 2xy) = 6x2 + 9xy – y2
⇒ M = (6x2 + 9xy – y2) – (5x2 – 2xy)
M = 6x2 + 9xy – y2 – 5x2 + 2xy
M = x2 + 11xy – y2
Câu 78: Hãy cho biết các tọa độ của điểm M nằm chính giữa một bức tường hình chữ nhật ABCD có cạnh AB = 5m, và cạnh AD = 4m. Lấy trục Ox dọc theo AB, trục Oy dọc theo AD.
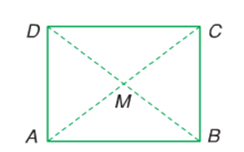
Lời giải:
Điểm M nằm chính giữa một bức tường hình chữ nhật ABCD nên M là giao điểm của hai đường chéo hình chữ nhật
Vậy tọa độ điểm M là:
Suy ra: M(2,5m; 2m)
Vậy tọa độ M có dạng M(2,5m; 2m).
Câu 79: Cho hình vẽ, biết a ⊥ c, b ⊥ c và . Chứng minh: a // b.
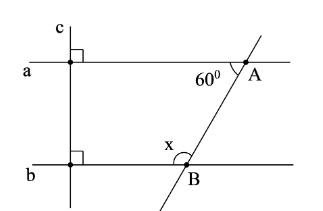
Lời giải:
Vì a ⊥ c, b ⊥ c nên a // b.
Câu 90: Biết . Tính giá trị biểu thức .
Lời giải:
⇒
⇔
⇔
Bình phương 2 vế ta được:
⇔
⇔
Vậy
Câu 91: Tính B = – 1 + 7 – 72 + 73 - … - 7200 + 7201 – 7202.
Lời giải:
B = – 1 + 7 – 72 + 73 - … - 7200 + 7201 – 7202
7B = – 7 + 72 – 73 + 74 - … - 7201 + 7202 – 7203
7B + B = (– 7 + 72 – 73 + 74 - … - 7201 + 7202 – 7203) + (– 1 + 7 – 72 + 73 - … - 7200 + 7201 – 7202)
8B = –7203 – 1
.
Câu 92: So sánh các số sau: 19920 và 200315
Lời giải:
19920 < 20020 = (23.52)20 = 260.540
200315 > 200015 = (2.103)15 = (24.53)15 = 260.545
Vì 260.545 > 260.540 nên 200315 > 19920.
Câu 93: So sánh 2 số sau: và .
Lời giải:
Ta có:
Mà:
Nên:
Vậy .
Câu 94: Cho A = 3 + 33 + 35 + … + 32021 + 32023. Chứng minh A chia hết cho 30.
Lời giải:
A = 3 + 33 + 35 + … + 32021 + 32023
A = (3 + 33) + (35 + 37) + … + (32021 + 32023)
A = 1.(3 + 33) + 34(3 + 33) + … +32020(3 + 33)
A = (3 + 33)(1 + 34 + … + 32020)
A = 30.(1 + 34 + … + 32020)
Vì 30 ⋮ 30 nên 30.(1 + 34 + … + 32020) ⋮ 30
Vậy A ⋮ 30.
Câu 95: Chứng minh vì sao số có ước lẻ là số chính phương.
Lời giải:
Gọi P là một số chính phương.
Ta có: P = k2 (k ∈ ℕ)
Giả sử k phân tích ra thừa số nguyên tố là k = ax.by.cz.... (a, b, c là các số nguyên tố)
⇒ P = (ax.by.cz....)2
⇒ P = a2x.b2y.c2z
Vì 2 chia hết cho 2 nên 2x, 2y, 2z, ... cũng chia hết cho 2
⇒ 2x, 2y, 2z, ... là số chẵn
Số lượng ước của P là (2x + 1)(2y + 1)(2z + 1)...
Vì 2x, 2y, 2z, ... là số chẵn nên 2x + 1, 2y + 1, 2z + 1, ... là số lẻ
⇒ (2x + 1)(2y + 1)(2z + 1)... là số lẻ
⇒ Số lượng ước của P là 1 số lẻ
Vậy số chính phương luôn có số ước là 1 số lẻ.
Câu 96: Hai số lẻ có tổng là số nhỏ nhất có 4 chữ số và ở giữa hai số lẻ đó có 4 số lẻ tìm hai số đó.
Lời giải:
Số nhỏ nhất có 4 chữ số là 1000. Vậy tổng 2 số là 1000.
Do ở giữa hai số lẻ đó có 4 số lẻ nữa nên giữa chúng có 5 khoảng và mỗi khoảng là 2 đơn vị.
Hiệu hai số là:
2.5 = 10
Số lớn là:
(1000 + 10) : 2 = 505
Số bé là:
505 – 10 = 495
Đáp số: 505 và 495.
Câu 97: Chứng minh tam giác ABC có ha = 2R.sinB.sinC.
Lời giải:
TH1: Tam giác ABC nhọn hoặc tam giác ABC tù ở A
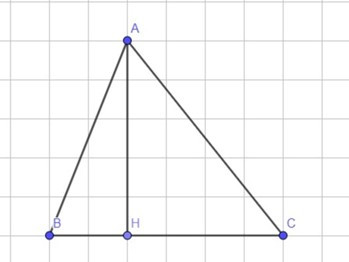
Ta có:
Suy ra: ha = AH = AC.sinC = b.sinC
Mà theo định lý sin: hay b = 2R.sinB
Suy ra: ha = 2R.sinB.sinC.
TH2: Tam giác ABC tù ở B hoặc C
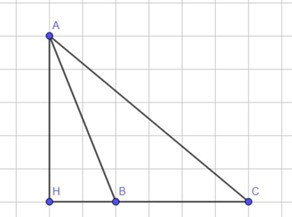
Ta có:
Suy ra: ha = AH = AB.sin
ha = AB.sin
ha = AB.sinB = c.sin B
Mà theo định lý sin: hay c = 2R.sinC
Vậy ha = 2R.sinB.sinC.
Câu 98: Một mảnh vườn hình chữ nhật có chu vi bằng chu vi của một thửa ruộng hình vuông cạnh 80m. Nếu giảm chiều dài mảnh vườn đi 30m và tăng chiều rộng thêm 10m thì mảnh vườn sẽ có hình vuông. Tính diện tích mảnh vườn?
Lời giải:
Chu vi của mảnh vườn hình chữ nhật là:
80 . 4 = 320 (m)
Nửa chu vi mảnh vườn hình chữ nhật là
320 : 2 = 160 (m)
Mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng là:
30 + 10 = 40 (m)
Chiều rộng mảnh vườn hình chữ nhật là:
(160 - 40) : 2 = 60 (m)
Chiều dài mảnh vườn hình chữ nhật là:
60 + 40 = 100 (m)
Diện tích mảnh vườn hình chữ nhật là:
60 . 100 = 6000 (m2).
Câu 99: Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O).
a) Chứng minh AB2 = AD.AE.
b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp, chứng minh HB là tia phân giác của .
Lời giải:
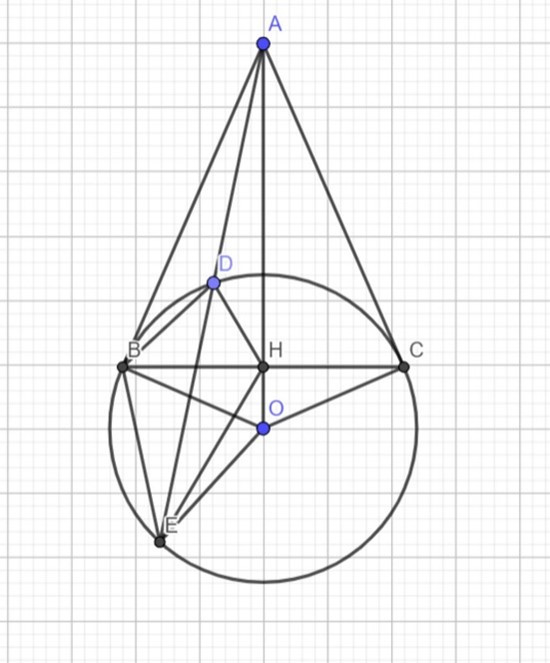
a) Xét tam giác ABD và tam giác ABE có:
Chung
(vì AB là tiếp tuyến (O))
⇒ ∆ABD ∽ ∆AEB (g.g)
⇒
⇒ AB2 = AD.DE
b) Ta có: AB,AC là tiếp tuyến của (O)
⇒AB ⊥ OB, BC ⊥ AO
⇒ BH ⊥ AO
⇒ AB2 = AH.AO (Hệ thức lượng trong tam giác vuông)
⇒ AH.AO = AD.AE
⇒
Mà
⇒ ∆ADH ∽ ∆AOE (c.g.c)
⇒
⇒ DHOE nội tiếp
⇒
⇒
Nên: HB là phân giác .
Câu 100: Cho . Tìm số nguyên x để M đạt GTNN.
Lời giải:
Để M nhỏ nhất thì nhỏ nhất
Suy ra: và x – 15 lớn nhất
Mà x – 15 là số nguyên nên x – 15 = -1
Suy ra: x = -1 + 15 = 14
Vậy GTNN của khi x = 14.
Đề bài. Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Điểm M nằm giữa B và C, gọi I là trung điểm của AC, lấy điểm N đối xứng M qua I.
a) Tính độ dài cạnh BC?
b) Tứ giác AMCN là hình gì? Vì sao?
Lời giải:
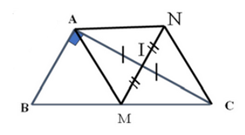
Ta có tam giác ABC vuông tại A, với AB = 6cm và AC = 8cm.
Sử dụng định lý Pythagoras, ta có: BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra: BC = 10 cm
Vậy độ dài cạnh BC là 10cm.
b) Vì N là điểm đối xứng của M qua I, nên ta có AI = IN và AM = MN.
Đồng thời, ta có IM = IN (tính chất đối xứng); IA = IC
Vậy ta có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Điều này chứng tỏ AMCN là hình bình hành.
Câu 101: Cho tứ diện ABCD có M nằm trên cạnh AB, N nằm trên cạnh AD thoả MB = 2MA, AN = 2ND. Gọi P là điểm thuộc miền trong của tam giác BCD. Tìm giao tuyến của (MNP) và (ABC).
Lời giải:
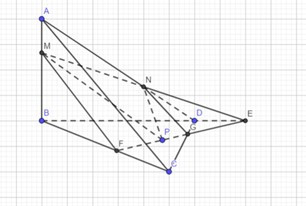
Dựng hình theo hình vẽ.
Ta có: MB = 2MA, AN = 2ND nên:
Nên MN không song song với BD
Gọi MN ∩ BD = E, EP ∩ BC = F
Suy ra: (MNP) ∩ (ABC) = MF.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.