Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 78) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 78)
Lời giải:
Chị Chi mua 50 cái bình hoa với số tiền là:
200.000 . 50 = 10.000.000 (đồng)
Chị mua 20 cái bình hoa với số tiền là:
200.000 . 20 = 4.000.000 (đồng)
Chị bán 20 cái bình hoa được số tiền là:
4.000.000 . (100% + 20%) = 4.800.000 (đồng)
Chị bán 30 cái bình hoa được số tiền là:
2.000.000 . 30 . (100% – 5%) = 5.700.000 (đồng)
Chị bán 50 cái áo được số tiền là:
4.800.000 + 5.700.000 = 10.500.000 (đồng)
Việc mua và bán 50 cái bình hoa, chị Chi lãi số tiền là:
10.500.000 – 10.000.000 = 500.000 (đồng)
Câu 2: Đặt tính rồi tính 157,25 : 3,7.
Lời giải:
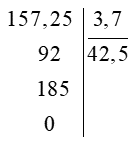
Ta có: 157,25 : 3,7 = 1572,5 : 37
Lấy 1572 : 37 = 42 (dư 18)
Hạ số 5 xuống được 185 : 37 = 5 (dư 0).
Lời giải:
Để đi từ A đến D ta phải đi từ A ⇒ B ⇒ C ⇒ D
Số cách đi từ A đến D là:
3 . 5 . 2 = 30
Số cách đi từ A đến D và quay lại A là:
302 = 900.
Vậy có 900 cách.
Lời giải:
Chọn A làm mốc, cho thời điểm 7 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương.
Ô tô chuyển động thẳng đều, ô tô xuất phát từ B cách A 30,5 km lúc 9 giờ (chuyển động sau xe máy 2 giờ) nên phương trình chuyển động của ô tô là:
y = 30,5 + 80(t – 2) = 80t – 129,5
Phương trình chuyển động của xe máy là y = 2t2 + 36
Ô tô đuổi kịp xe máy tại thời điểm hai đồ thị hàm số giao nhau.
Xét phương trình hoành độ:
2t2 + 36 = 80t – 129,5
⇔ 2t2 – 44t + 129,4 = 0
⇔ [t=18,5(L)t=3,5
Khi t = 3,5 thì y = 150,5
Vậy ô tô đuổi kịp xe máy tại vị trí cách B là: 150,5 − 30,5 = 120 km.
Lời giải:
Hiện nay anh hơn em 13 tuổi thì 7 năm nữa hiệu số tuổi không đổi và anh vẫn hơn em 13 tuổi.
Coi tuổi anh khi đó là 2 phần thì tuổi em là 1 phần như thế
Tuổi anh khi đó là :
13 : (2 – 1) . 2 = 26 (tuổi)
Tuổi em khi đó là:
26 – 13 = 13 (tuổi)
Tuổi anh hiện tại là:
26 – 7 = 19 (tuổi)
Tuổi em hiện tại là:
19 – 13 = 6 (tuổi)
Vậy năm ngoái tuổi em là 5 tuổi, tuổi anh là 18 tuổi.
Năm ngoái tuổi anh gấp số lần tuổi em là:
18 : 5 = 3,6 (lần).
Câu 6: Một thửa đất hình chữ nhật có chu vi là 648m. Chiều rộng kém chiều dài 72m.
a) Tính diện tích thửa đất đó.
b) Một thửa đất hình vuông có chu vi bằng chu vi thửa đất trên. Tính diện tích thửa đất hình vuông.
Lời giải:
a) Nửa chu vi hình chữ nhật đó là:
648 : 2 = 324(m)
Chiều rộng thửa đất đó là:
(324 – 72) : 2 = 126(m)
Chiều dài thửa đất đó là:
126 + 72 = 198(m)
Diện tích thửa đất đó là:
126 . 198 = 24948 (m2)
b) Cạnh thửa đất hình vuông là:
648 : 4 = 162 (m)
Diện tích thửa đất đó là:
162 . 162 = 26244 (m2).
Lời giải:
Giải thích các bước giải:
Gọi x, y lần lượt là số ghe lớn, ghe nhỏ cần thuê. (x, y ≥ 0)
Số hành khách để x ghe lớn và y ghe nhỏ chở là: 10x + 5y
Số vali để x ghe lớn và y ghe nhỏ chở là: 4x + 4y
Chi phí thuê ghe là T = 250x + 130y (nghìn đồng)
Từ các dữ kiện ta có hệ phương trình:
{0≤x≤80≤y≤810x+5y≥404x+4y≥24 (1)
Khi đó bài toán mới hình thành:
Trong các nghiệm của hệ bất phương trình (1) thì nghiệm (x = x0; y = y0) nào cho T = 250x + 130y nhỏ nhất.
Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE tính cả biên (như hình vẽ).
T đạt giá trị nhỏ nhất tại một trong các đỉnh của ngũ giác ABCDE
Ta có:
A(0;8) ⇒ T = 1040
B(8;8) ⇒ T = 3040
C(8;0) ⇒ T = 2000
D(6;0) ⇒T = 1500
E(2;4) ⇒ T = 1020
Do đó T = 250x + 130y nhỏ nhất là 1020 (nghìn đồng) khi x = 2; y = 4
Vậy chủ khách sạn cần thuê 2 ghe lớn và 4 ghe nhỏ để chi phí thấp và phải trả là 1020 nghìn đồng.
a) Một công ty muốn đặt hoa khai trương nên đã đặt 30 bó hoa. Tính số tiền công ty đó mua biết giá ban đầu của 1 bó là 60000 đồng.
b) 1 khách hàng đã mua hoa hướng dương ở tiệm chị H và tổng số tiền người đó phải trả là 648000 đồng. Hỏi người đó mua bao nhiêu bó?
Lời giải:
a) 10 bó hoa đầu tiên công ty được tính với giá 1 bó hoa bằng 80% giá ban đầu là 48000 đồng, từ bó thứ 11 trở đi, công ty được tính giá 1 bó hoa là 24000 đồng
Tổng số tiền công ty đó mua là:
10 . 48000 + 20 . 24000 = 960000 (đồng)
b) Sau khi trả tiền cho 10 bó hoa đầu thì số tiền khách hàng trả cho những bó hoa còn lại là:
648000 – 10 . 48000 = 168000 (đồng)
Sau khi mua 10 bó hoa đầu thì số bó hoa khách hàng mua thêm là:
168000 : 24000 = 7 (bó).
Câu 9: Kể tên các khối tròn xoay đã học? Lấy ví dụ trong thực tế.
Lời giải:
Khối tròn xoay:
+ Hình trụ đáy tròn: Cây nến, bóng đèn ống (không kể chân bóng), viên pin, hộp sữa, ...
+ Hình nón: Đầu tên lửa, đầu đạn, ...
+ Hình cầu: Viên bi, qua bóng, ...
Câu 10: Tìm ước chung lớn nhất của 11, 13, 17, 19.
Lời giải:
Do 11; 13; 17; 19 là các số nguyên tố nên ƯCLN (11; 13; 17; 19) = 1.
Vậy ƯCLN (11; 13; 17; 19) = 1.
Lời giải:
Nửa chu vi của đáy bể hình chữ nhật là:
7,6 : 2 = 3,8 (m)
Chiều dài đáy bể là:
(3,8 + 0,8) : 2 = 2,3 (m)
Chiều rộng đáy bể là:
2,3 − 0,8 = 1,5 (m)
Thể tích của bể nước là:
2,3 . 1,5 . 2 = 6,9 (m3)
Đổi 6,9m3 = 6900dm3 = 6900 lít
Đáp số: 6900 lít.
Lời giải:
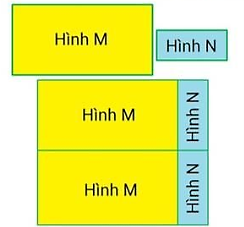
Cạnh hình vuông ghép là:
3232 : 4 = 808 (cm)
Dựa vào hình vẽ, ta thấy cạnh hình vuông ghép bằng tổng chiều dài hình M và chiều rộng hình N
Mà ta có chiều dài hình M lớn chiều rộng hình N là 570 cm nên chiều dài hình M là:
(808 + 570) : 2 = 689 (cm)
Tiếp tục dựa vào hình vẽ, ta thấy cạnh hình vuông ghép bằng hai lần chiều rộng hình M, nên chiều rộng hình M là:
808 : 2 = 404 (cm)
Chu vi hình M là:
(689 + 404) . 2 = 2186 (cm) = 21,86 (m)
Đáp số: 21,86 (m).
Câu 13: Cho tập hợp A = {1; 2; 3; 4; 5}. Có bao nhiêu cặp thứ tự (x; y) biết rằng:
b) (x; y) là tập con của A.
c) x và y đều thuộc A sao cho x + y = 6.
Lời giải:
a) Tập A có 5 phần tử
Số cách chọn x là 5 cách
Số cách chọn y là 5 cách (do không yêu cầu x, y khác nhau)
Số cặp thỏa mãn là: 5 . 5 = 25 (cặp)
b) (x; y) là tập con của A
Do có sắp thứ tự nên có A25=20 cặp.
c) Để x + y = 6 = 1 + 5 = 2 + 4 = 3 + 3
Vậy có 5 cặp số (x; y) thỏa mãn là (1; 5), (5; 1), (2; 4), (4; 2), (3; 3).
Câu 14: Giao điểm của ba đường phân giác gọi là gì?
Lời giải:
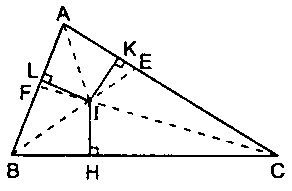
Giao điểm của ba đường phân giác gọi là tâm đường tròn nội tiếp tam giác.
Ba đường phân giác của một tam giác đồng quy tại 1 điểm. Điểm này cách đều ba cạnh của tam giác đó.
Ví dụ:
Câu 15: Tìm số bị chia và số chia bé nhất để phép chia đó có thương là 123 và số dư là 44.
Lời giải:
Số chia nhỏ nhất trong phép chia đã cho là:
44 + 1 = 45
Số bị chia nhỏ nhất trong phép chia đã cho là:
45 . 123 + 44 = 5579
Đáp số: 5579.
Câu 16: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OC = 2cm. Tính AC ?
Lời giải:
Vì AC, BD là đường chéo của hình chữ nhật nên cắt nhau tại trung điểm của mỗi đường. Suy ra: AC = 2OC = 2.2 = 4 cm.
Vậy AC = 4cm.
Lời giải:
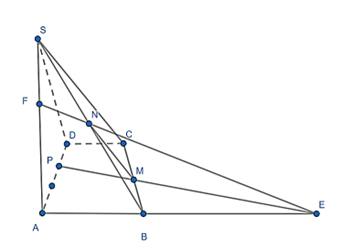
Ta có: M, N là trung điểm BC; SB nên MN là đường trung bình của tam giác SCB
Suy ra: MN // SC
Mà SC ∈ (SCD) nên MN // (SCD)
+) Gọi giao điểm của PM và AB là E
Ta có: E ∈ AB ⸦ (SAB), E ∈ PM ⸦ (MNP)
Giao điểm của EN và SA là F
Mà EN ⸦ (MNP)
Suy ra: SA ∩ (MNP) = {F}.
Lời giải:
Tổng tiền mua cam:
500 . 40000 = 20000000 (đồng)
Tổng tiền vốn là:
20000000 + 4000000 = 24000000 (đồng)
Số lượng cam không bị hư là:
500.(100% − 10%) = 500 . 90% = 450 (kg)
Tổng số tiền thu được khi bán hết là:
(100% + 20%) . 24000000 = 28800000 (đồng)
Giá bán của mỗi kg cam là:
28800000 : 450 = 64000 (đồng)
Vậy giá bán của mỗi kg cam là: 64000 đồng.
Câu 19: Có bao nhiêu số nguyên sau khi làm tròn trăm cho kết quả là 6700?
Lời giải:
Có khoảng 100 số từ 6650 đến 6749.
Để làm tròn đến số 6700 thì số đó nhỏ nhất phải là:6650 vì 6649 làm tròn hàng trăm sẽ thành 6600.
Và số lớn nhất sẽ bằng 6749 vì nếu là 6750 thì làm tròn đến hàng phần trăm sẽ bằng 6800.
Vậy có khoảng 100 số nguyên sau khi làm tròn bằng 6700.
Câu 20: Nêu công thức tính diện tích hình bình hành.
Lời giải:
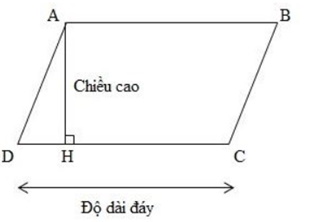
Công thức tính diện tích của hình bình hành sẽ bằng tích của cạnh đáy nhân với chiều cao.
Câu 21: Tìm GTNN của P = x2 + 2y2 + 2xy – 6x – 8y + 2024.
Lời giải:
P = x2 + 2y2 + 2xy – 6x – 8y + 2024
P = x2 + y2 + y2 + 2xy – 6x – 6y – 2y + 2024
P = (x2 + 2xy + y2) – (6x + 6y) + 9 + y2 – 2y + 1 + 2014
P = (x + y)2 – 2(x + y)3 + 32 + (y – 1)2 + 2014
P = (x + y – 3)2 + (y – 1)2 + 2014
Ta thấy (x + y – 3)2 + (y – 1)2 ≥ 0 với mọi x, y
Nên P ≥ 2014
Vậy GTNN của P là 2014 khi {x+y=3y−1=0 ⇔ {x=2y=1 .
Lời giải:
y = ax + 3 đi qua A(– 1; 2) nên ta có:
2 = – a + 3
⇔ a = 3 – 2
⇔ a = 1
Vậy hệ số góc của đường thẳng trên là 1.
Lời giải:
Để bó hoa có đúng 1 bông hồng đỏ thì ta chọn 1 hoa đỏ trong 4 bông hoa đỏ, 6 bông còn lại chọn bất kỳ trong 8 bông vàng và trắng
Số cách chọn là: C14.C68=112 (cách).
Câu 24: Tính giá trị biểu thức: (– 15).67 – 85.(– 33).
Lời giải:
(– 15).67 – 85.(– 33)
= – 1005 – (– 2805)
= – 1005 + 2805
= 1800.
Câu 25: Tìm giá trị của m để 2x2 + 3x + m + 1 > 0 với mọi x ∈ ℝ
Lời giải:
Xét f(x) = 2x2 + 3x + m + 1 là tam thức bậc hai với a = 2, b = 3, c = m + 1.
Ta có: ∆ = 32 – 4.2.(m + 1) = 9 – 8m – 8 = 1 – 8m.
Vì a = 2 > 0 nên để 2x2 + 3x + m + 1 > 0 với mọi x ∈ ℝ thì ∆ < 0
⇔ 1 – 8m < 0
⇔ m > 1818.
Vậy với m > 1818 thì 2x2 + 3x + m + 1 > 0 với mọi x ∈ ℝ.
Câu 26: Các số chia hết cho 2 có tận cùng là chữ số nào?
Lời giải:
Các số tận cùng bằng 0, 2, 4, 6, 8 thì chia hết cho 2.
Ví dụ: 12, 10, 24, 36, 48 là các số chia hết cho 2 vì có tận cùng là 0, 2, 4, 6, 8.
Lời giải:
1 cm3 = 10-3 dm3 = 10-6 m3 = 0,000001 m3
Như vậy để đổi cm3 sang m3 trên máy tính ta lấy đơn vị cm3 nhân với 10-6 hoặc chia cho 1000000.
Câu 28: Cách làm tròn độ, phút, giây.
Lời giải:
1 độ = 60 phút; 1 phút = 60 giây
Nên chỉ cần ≥ 30 phút thì cộng 1 độ
Nếu ≥ 30 giây thì cộng 1 phút
Ví dụ: 30°32'43''
Làm tròn đến độ: 31°
Làm tròn đến phút: 30°33'
Lời giải:
Chia 9 viên bi thành 3 nhóm, mỗi nhóm 3 quả.
Gọi tên 3 nhóm là N1, N2, N3
- Lần cân 1, đặt N1 và N2 lên 2 đĩa cân.
Có 2 khả năng xảy ra:
Khả năng 1: Cân thăng bằng ⇒ Quả nhẹ hơn sẽ ở N3
Khă năng 2: Cân không thăng bằng ⇒ Đĩa cân trong 1 trong 2 nhóm N1 và N2 đĩa nào bổng hơn thì viên bi ở đó
- Lần cân 2:
Khả năng 1: Ta đặt 2 trong 3 viên bi trong N3 lên ⇒ Có 2 trường hợp:
TH1: Cân thăng bằng ⇒ Viên bi nhẹ hơn sẽ là viên còn lại
TH2:Cân không thăng bằng ⇒Viên bi nhẹ hơn sẽ bổng lên
Khả năng 2: Giả sử đĩa bổng hơn thuộc N1
Ta đặt 2 trong 3 viên bi thuộc N1 lên 2 đĩa cân ⇒ Có 2 trường hợp:
TH1: Cân thăng bằng ⇒ Viên bi nhẹ hơn sẽ là viên còn lại
TH2:Cân không thăng bằng ⇒ Viên bi nhẹ hơn sẽ bổng lên
Vậy sau ít nhất 2 lần cân, ta tìm ra được viên bi nhẹ hơn.
Lời giải:
Tổng số tấn đội xe chở vật liệu là:
2,8 . 20 = 56 (tấn).
Số chuyến nếu mỗi chuyến xe chở 4 tấn là:
56 : 4 = 14 (chuyến).
Lời giải:
Ta có: Sn = n2 + 4n
S1 = u1 = 1 + 4 . 1 = 5
S2 = u1 + u2 = 22 + 4 . 2 = 12
u2 = 12 – 5 = 7
Công sai d = u2 – u1 = 7 – 5 = 2
Vậy un = u1 + (n – 1).d = 5 +(n – 1).2 = 2n + 3.
Câu 32: Với các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số?
Lời giải:
Mỗi số tự nhiên có 6 chữ số khác nhau là một cách sắp xếp 6 chữ số hay một hoán vị của 6 phần tử:
Vậy có P6 = 6! = 720 (số).
Lời giải:
Diện tích mặt bàn là:
(180 + 240) . 160 : 2 = 33600 (cm2).
Số tiền mua gỗ để đóng mặt bàn đó:
33600. 200 = 6720000 (đồng).
Vậy bác Đức cần 6720000 đồng mua gỗ để đóng mặt bàn đó.
Lời giải:
Qua điểm M ở ngoài đường thẳng a, có có thể vẽ được 1 và chỉ 1 đường thẳng đi qua M và vuông góc với đường thẳng a.
Lời giải:
Chiều cao của thửa ruộng hình tam giác đó là:
55,8 . 70 : 100 = 39,06 (m)
Diện tích thửa ruộng hình tam giác đó là:
55,8 . 39,06 : 2 = 1089,774 (m2)
Đáp số : 1089,774 m2.
Câu 36: Sân nhà bạn An là hình chữ nhật có chu vi là 30m và chiều rộng 5m.
a. Tính diện tích sân nhà bạn An.
Lời giải:
a) Nửa chu vi của sân nhà bạn An là :
30 : 2 = 15 (m)
Chiều dài của sân nhà bạn An là :
15 – 5 = 10 (m)
Diện tích của sân nhà bạn An là :
10 . 5 = 50 (m²)
b) Đổi 50m² = 500000cm²
Diện tích của viên gạch hình vuông là :
50 . 50 = 2500 (cm²)
Bố An cần dùng số viên gạch để lát sân đó là :
500000 : 2500 = 200 (viên gạch)
Đáp số : a) 50 m²
b) 200 viên gạch
Lời giải:
Chọn một cạnh của đa giác (H) làm cạnh của tam giác nên có 20 cách
Chọn một đỉnh (để ghép với cạnh đã chọn ở bước trên tạo thành tam giác thỏa mãn bài toán) nên có 16 cách chọn (bỏ 2 đỉnh thuộc cạnh đã chọn và 2 đỉnh liền kề hai bên cạnh đã chọn).
Vậy số tam giác cần tìm là 20 . 16 = 320.
Lời giải:
Ta có:
u2 – u3 + u5 = 10
⇔ u1 + d − (u1 + 2d) + u1 + 4d = 10
⇔ u1 + 3d = 10 (1)
Ta có:
u1 + u6 = 17
⇔ u1 + u1 + 5d = 17
⇔ 2u1 + 5d = 17 (2)
Từ (1) và (2) ta có hệ:
{u1+3d=102u1+5d=17 ⇔ {u1=1d=3
Vậy cấp số cộng đã cho có u1 = 1 và công sai d = 3.
Câu 39: Cho hình bình hành ABCD.Lấy điểm I trên cạnh AB, điểm K trên cạnh CD sao cho AI = CK.
1. Chứng minh tứ giác AICK là hình bình hành.
3. Chứng minh AC, BP, DQ đồng quy.
Lời giải:
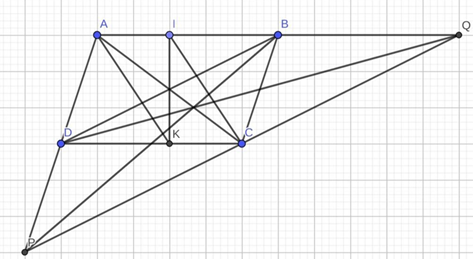
1. Ta có AB // CD ⇒ AI // CK
Mà AI = KC
⇒ AICK là hình bình hành
2. Ta có ABCD là hình bình hành ⇒AD // BC, AB // CD
⇒ DP // CB, DC // BQ
Mà CP // BD, CQ // BD
⇒ CBDP, CDBQ là hình bình hành
⇒ CP = DB,CQ = BD
⇒ CP = CQ
⇒ C là trung điểm PQ
3. Ta có CBDP, CDBQ là hình bình hành
⇒ BQ = CD = AB, DP = BC = AD
⇒ B, D là trung điểm AQ, AP
Mà C là trung điểm PQ
⇒ AC, BP, QD đồng quy
Lời giải:
Trong một ngày đêm kim giờ quay hai vòng
Vậy trong một ngày đêm đồng hồ đó đánh
(1 + 2 + ... + 12) . 2 = 12 . (12 + 1) = 156 tiếng.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.