Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44)

Ngọc Nguyễn Ngày: 13-07-2023 Tổng hợp kiến thức

341

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44)

Câu 1: Cả ba con gà, vịt, ngỗng cân nặng 10,5 kg. Biết con gà cân nặng 1,5 kg, vịt nặng hơn gà 0,9 kg. Hỏi con ngỗng cân nặng bao nhiêu ki-lô-gam?

Lời giải:

Con vịt nặng số ki-lô-gam là:

1,5 + 0,9 = 2,4 (kg)

Gà và vịt cân nặng số ki-lô-gam là:

1,5 + 2,4 = 3,9 (kg)

Con ngỗng cân nặng số ki-lô-gam là:

10,5 – 3,9 = 6,6 (kg)

Đáp số: 6,6kg.

Câu 2: Tính chiều cao ứng với cạnh 40 cm của một tam giác, biết góc kề với cạnh này bằng 40° và 55°.

Lời giải:

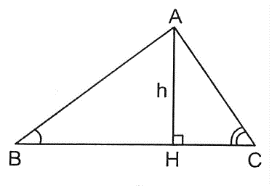
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 1)

BH = h . cotB; CH = h . cot C

Suy ra BC = BH + CH = h(cot B + cot C).

Do đó $h = \frac{40}{\cot 40 ° + \cot 55 °} \approx \frac{40}{1,1918 + 0,7002} \approx \frac{40}{1,892} \approx 21$ (cm).

Câu 3: Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y = (m + 2)x + 2m² + 1 tìm m để hai đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Lời giải:

Để 2 đường thẳng (d) và (d') cắt nhau trên trục tung thì x = 0

Ta có : (d): y = 2m² + 1

(d'): y = 3.0 + 3 = 3

Vì (d) ∩ (d') nên 2m² + 1 = 3

Do đó m = 1 hoặc m = − 1.

Câu 4: Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng và trục Ox bằng 45°.

Lời giải:

Vì hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0 hay $m \neq \frac{- 1}{2}$ .

Gọi góc α là góc tạo bởi đường thẳng và trục Ox . Theo giả thiết α = 45°.

Ta có: tan α = a

⇒ tan 45° = 2m + 1

⇒ 1 = 2m + 1

⇒ 0 = 2m

⇒ m = 0.

Vậy m = 0.

Câu 5: Cho hàm số y = (2m – 1)x + 2. Tìm m để:

a) Hàm số đã cho là hàm số bậc nhất;

b) Hàm số đã cho là hàm số đồng biến;

c) Đồ thị hàm số đi qua 2 điểm A (2; 4);

d) Đồ thị hàm số song song với đường thẳng y = 3x.

Lời giải:

a) Để hàm số đã cho là hàm số bậc nhất thì 2m – 1 ≠ 0 hay m ≠ $\frac{1}{2}$ .

b) Để hàm số đã cho là hàm số đồng biến thì 2m – 1 ≥ 0 hay m ≥ $\frac{1}{2}$ .

c) Để đồ thị hàm số đi qua 2 điểm A (2; 4) thì:

Thay vào x = 2; y = 4 ta có:

4 = 4m – 2 + 2

4 = 4m

m = 1

d) Do đồ thị hàm số y song song với đường thẳng y = 3x, nên ta có:

2m – 1 = 3

⇒ 2m = 4

⇒ m = 2

Câu 6: Người ta trồng mía trên một khu đất hình chữ nhật có chiều rộng 130m, chiều dài hơn chiều rộng 70 m. Biết rằng, trung bình cứ 100 thu hoạch được 300kg mía. Hỏi khu đất đó thu hoạch được bao nhiêu kg mía?

Lời giải:

Chiều dài khu đất là:

130 + 70 = 200 (m)

Diện tích khu đất là:

200 × 130 = 26 000 (m²)

26 000 m² gấp 100 m² số lần là:

26 000 : 100 = 260 (lần)

Trên cả khu đất đó người ta thu hoạch được số tấn mía là:

300 × 260 = 78 000 (kg)

Đáp số: 78 000 kg.

Câu 7: Có một số tiền, nếu mua kẹo loại 5 000 đồng một gói thì được 15 gói kẹo. Hỏi cùng số tiền đó nếu mua loại kẹo 7 500 đồng một gói thì được bao nhiêu gói kẹo?

Lời giải:

Có tất cả số tiền là:

5000 × 15 = 75 000 (đồng)

Với số tiền đó nếu mua kẹo loại 7 500 đồng thì được số gói là:

75 000 : 7 500 = 10 (gói)

Đáp số: 10 gói.

Câu 8: Một gia đình gồm bố, mẹ và hai con (4 người), bình quân thu nhập hằng tháng là 2 000 000 đồng một người. Nếu gia đình đó thêm một con nữa thì bình quân thu nhập hằng tháng của mỗi người bị giảm bao nhiêu tiền, biết rằng tổng thu nhập không thay đổi?

Lời giải:

Số người trong gia đình là

4 + 1 = 5 (người)

Tổng thu nhập hàng tháng của gia đình (4 người) là:

2 000 000 × 4 = 8 000 000 (đồng)

Bình quân thu nhập hàng tháng của 1 người khi gia đình có thêm một con là:

8 000 000 : 5 = 1 600 000 (đồng)

Bình quân thu nhập hàng tháng của 1 người bị giảm khi gia đình có thêm con:

2 000 000 – 1 600 000 = 400 000 (đồng)

Đáp số: 400 000 đồng.

Câu 9: Một lớp có 60 học sinh, trong đó có 36 học sinh giỏi toán, 21 học sinh giỏi văn, 25 học sinh giỏi anh, 10 học sinh vừa giỏi toán vừa giỏi văn, 15 học sinh vừa giỏi toán vừa giỏi anh, 4 học sinh vừa giỏi văn vừa giỏi anh, 5 học sinh giỏi cả 3 môn. Hỏi trong lớp có mấy học sinh chỉ giỏi 1 môn, mấy học sinh không giỏi môn nào trong 3 môn trên?

Lời giải:

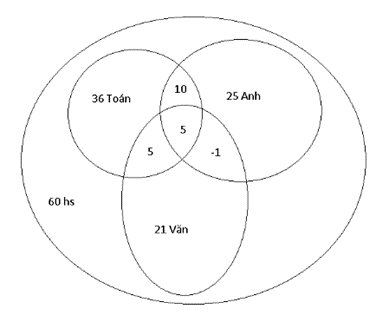
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 2)

Số học sinh học giỏi chỉ giỏi môn Toán là:

36 – 10 – 5 – 5 = 16 (học sinh)

Số học sinh học giỏi chỉ giỏi môn Anh là:

25 – 5 – 10 + 1 = 11 (học sinh)

số học sinh học giỏi chỉ giỏi môn Văn là:

21 – 5 – 5 + 1 = 12 (học sinh)

Lớp đó có số học sinh không giỏi môn nào trong 3 môn trên là :

60 – ( 6 + 11 + 12 + 10 + 5 + 5 – 1) = 2 (học sinh).

Vậy lớp đó có số học sinh không giỏi môn nào trong 3 môn trên là 2 học sinh.

Câu 10: Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng $\frac{1}{2}$ số quả táo. Số quả xoài gấp 3 lần số quả cam. Tính số quả táo.

Lời giải:

Ta có sơ đồ:

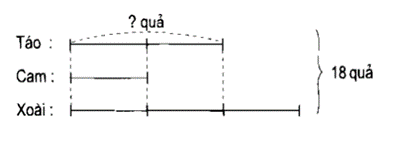
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 3)

Theo sơ đồ, tổng số phần bằng nhau là:

2 + 1 + 3 = 6 (phần)

Số quả táo là:

18 : 6 × 2 = 6 (quả)

Đáp số: 6 quả

Câu 11: Tổng của hai số là 90. Số thứ nhất bằng $\frac{7}{8}$ số thứ hai. Tìm hai số đó.

Lời giải:

Ta có sơ đồ:

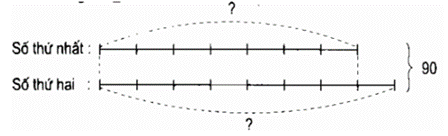
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 4)

Theo sơ đồ, tổng số phần bằng nhau là:

7 + 8 = 15 (phần)

Số thứ nhất là:

90 : 15 × 7 = 42

Số thứ hai là:

90 – 42 = 48

Đáp số: số thứ nhất là 42; số thứ hai là 48

Câu 12: Tính giá trị của biểu thức P = 18a + 30b + 7a – 5b. Biết a + b = 100

Lời giải:

P = 18a + 30b + 7a − 5b

= (18a + 7a) + (30b − 5b)

= 25a + 25b

= 25 . (a + b)

Thay a + b = 100 vào biểu thức P ta được :

25 . 100 = 2 500

Câu 13: Cho a, b, c > 0 thỏa mãn a² + b² + c² = 3. Tìm GTNN của: A = a³ + b³ + c³

Lời giải:

Áp dụng BĐT Cauchy cho các số dương ta có:

$a^{3} + a^{3} + 1 \geq 3 \sqrt[3]{a^{6}} = 3 a^{2} b^{3} + b^{3} + 1 \geq 3 \sqrt[3]{b^{6}} = 3 b^{2} c^{3} + c^{3} + 1 \geq 3 \sqrt[3]{c^{6}} = 3 c^{2}$

Cộng theo vế các BĐT vừa thu được ta có:

2(a³ + b³ + c³) + 3 ≥ 3(a² + b² + c²)

⇔ 2A + 3 ≥ 9

⇔ A ≥ 3

Dấu “ = ” xảy ra khi a = b = c = 1.

Vậy A_min = 3 khi và chỉ khi a = b = c = 1.

Câu 14: Tìm x, biết: x⁵ = x³.

Lời giải:

x⁵ = x³

x⁵ − x³ = 0

x³(x² – 1) = 0

x³(x – 1)(x + 1) = 0

x³ = 0 hoặc x – 1 = 0 hoặc x + 1 = 0

x = 0 hoặc x = 1 hoặc x = – 1

Vậy x ∈ {– 1; 0; 1}.

Câu 15: Trước đây mua 5 m vải phải trả 60 000 đồng. Hiện nay giá bán mỗi mét vải đã giảm 2000 đồng. Hỏi với 60 000 đổng, hiện nay có thể mua được bao nhiêu mét vải như thế ?

Lời giải:

Trước đây mua 5 m vải phải trả 60 000 đồng nên mỗi mét vải có giá là:

60 000 : 5 = 12 000 (đồng)

Hiện nay giá bán mỗi mét vải đã giảm 2 000 đồng nên giá mỗi mét vải hiện nay là:

12 000 – 2 000 = 10 000 (đồng)

Hiện nay giá mỗi mét vải là 10 000 đồng nên với 60 000 đồng có thể mua được số mét vải là :

60 000 : 10 000 = 6 (m)

Đáp số: 6 mét vải.

Câu 16: Trung bình mỗi con gà đẻ ăn hết 104 g thức ăn trong một ngày. Hỏi trại chân nuôi cần bao nhiêu ki-lô-gam thức ăn cho 375 con gà máu để ăn trong 10 ngày?

Lời giải:

Số thức ăn trại chăn nuôi cần trong 1 ngày là:

104 × 375 = 39000 (g)

39000 (g) = 39 (kg)

Số thức ăn trại chăn nuôi cần trong 10 ngày là:

39 × 10 = 390 (kg)

Đáp số: 390 kg.

Câu 17: Phân tích đa thức thành nhân tử: x² – y² + 12y – 36.

Lời giải:

x² – y² + 12y – 36

= x² – (y² – 2y + 36)

= x² – (y – 6)²

= (x – y + 6)( x + y – 6).

Câu 18: Cho tam giác ABC có 3 góc nhọn, trực tâm H. Đường thẳng vuông góc với AB kẻ từ B cắt đường thẳng vuông góc với AC kẻ từ C tại D .

a) Chứng minh tứ giác BHCD là hình bình hành.

b) Gọi M là trung điểm BC, O là trung điểm AD. Chứng minh 2OM = AH.

Lời giải:

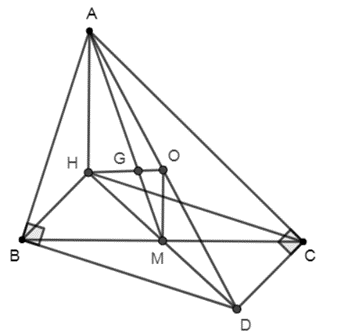
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 5)

a) Gọi AD và BE lần lượt là hai đường cao của ∆ABC .

Theo đề hai đường cao AD và BE cắt nhau tại H hay H là trực tâm của ∆ABC

⇒ CH là đường cao thứ 3 của ∆ABC

Do đó CH ⊥ AB (1)

mà BD ⊥ AB (gt) ⇒ CH // BD

Có BH ⊥ AC (BE là đường cao)

CD ⊥ AC

Do đó BH // CD (2)

Từ (1) và (2) suy ra : Tứ giác BHCD là hình bình hành

b) Có BHCD là hình bình hành nên 2 đường chéo cắt nhau tại trung điểm mỗi đường mà M là trung điểm của BC ⇒ M cũng là trung điểm của HD hay HM = DM

Có O là trung điểm của AD hay OA = OD

Xét ∆AHD có: HM = DM; OA = OD

Suy ra OM là đường trung bình của ∆AHD.

Do đó OM = $\frac{1}{2}$ AH hay AH = 2OM.

Câu 19: Một người có số tiền không quá 70 000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá: loại 2 000 đồng và loại 5 000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5 000 đồng?

Lời giải:

Gọi x là số tờ giấy bạc loại 5 000 đồng người đó có (0 < x < 15, x ∈ N).

Vì tổng số tờ 2 000 đồng và 5 000 đồng là 15 tờ nên ta có điều kiện x < 15

Và số tờ 2 000 đồng người đó có là: 15 – x (tờ)

Khi đó, tổng số tiền người đó có là: 5 . x + 2 . (15 – x) (nghìn đồng).

Theo bài ra, người đó có số tiền không quá 70 000 đồng nên ta có bất phương trình:

5 . x + 2 . (15 – x) ≤ 70

⇔ 5x + 30 – 2x ≤ 70

⇔ 3x ≤ 70 – 30

⇔ 3x ≤ 40

$\Leftrightarrow x \leq \frac{40}{3}$ .

Kết hợp với điều kiện trên nên x có thể nhận một trong các giá trị {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}.

Câu 20: Lớp 5A có 43 học sinh. Trong bài thi học kỳ một cả lớp đều được điểm 9, hoặc điểm 10. Tổng số điểm của cả lớp là 406 điểm. Hỏi có bao nhiêu bạn được điểm 9, bao nhiêu bạn được điểm 10?

Lời giải:

Nếu cả lớp đều đạt điểm 9.

Khi đó, tổng số điểm của lớp là :

43 × 9 = 387 (điểm)

406 điểm thì hơn 387 điểm là :

406 – 387 = 19 (điểm)

Số học sinh được điểm 10 là :

19 : (10 – 9) = 19 (học sinh)

Số học sinh được điểm 9 là :

43 – 19 = 24 (học sinh).

Đáp số: 19 học sinh được điểm 10, 24 học sinh được điểm 9.

Câu 21: Cho các số 0; 1; 2; 3; 4; 5; 6; 7. Từ các chữ số trên lập được bao nhiêu số có 4 chữ số đôi một khác nhau và chia hết cho 10.

Lời giải:

Các số thỏa mãn điều kiện đề bài có dạng $\bar{a b c 0}$

Chọn 3 chữ số khác nhau từng đôi một từ {1; 2; 3; 4; 5; 6; 7} và xếp vào 3 vị trí

Do đó có $A_{7}^{3} = 210$ (cách).

Vậy có 210 số thỏa mãn điều kiện đề bài.

Câu 22: Một mảnh đất hình chữ nhật có nửa chu vi là 194 m chiều dài gấp 3 lần chiều rộng. Trên mảnh đất đó, người ta dành phần đất hình vuông cạnh 16,5 m để làm nhà.

a) Tính diện tích mảnh đất đó?

b) Tính diện tích cách làm nhà?

Lời giải:

a) Tính diện tích mảnh đất:

Chiều dài mảnh đất đó là :

194 : (3 + 1) × 3 = 1 455 (m)

Chiều rộng mảnh đất đó là :

194 – 45,5 = 485 (m)

Diện tích mảnh đất đó là :

145,5 × 48,5 = 7 056,75 (m²)

b) Tính diện tích mảnh đất làm nhà:

Diện tích đất làm nhà là :

16,5 × 16,5 = 272,25 (m²)

Diện tích mảnh đất: 7 056,75 (m²)

Diện tích mảnh đất làm nhà: 272,25 (m²)

Đáp số: a) 7 056,75 m²;

b) 272,25 m².

Câu 23: Một can nhựa chứa 100 lít dầu hỏa. Biết một lít dầu hỏa cân nặng 0,8 kg, can rỗng cân nặng 12,5 kg. Hỏi can dầu hỏa đó cân nặng bao nhiêu ki-lô-gam?

Lời giải:

100 lít dầu hỏa nặng số ki-lô-gam là:

0,8 × 100 = 80 (kg)

Can dầu hỏa đó nặng số ki-lô-gam là:

80 + 12,5 = 92,5 (kg)

Đáp số: 92,5 kg.

Câu 24: Một mảnh vải 4 m có giá 192 000 đồng. Một người mua 1,25 m vải đó để may áo với giá tiền công may áo là 30 000 đồng. Hỏi toàn bộ số tiền may chiếc áo đó là bao nhiêu?

Lời giải:

Giá của 1 mét vải là:

192 000 : 4 = 48 000 (đồng)

Giá của 1,25 mét vải là:

48 000 × 1,25 = 60 000 (đồng)

Toàn bộ số tiền may chiếc áo đó là:

60 000 + 30 000 = 90 000 (đồng)

Đáp số: 90 000 đồng

Câu 25: Một hình chữ nhật có nửa chu vi là 61,5 m, chiều rộng bằng $\frac{2}{3}$ chiều dài. Tính diện tích hình chữ nhật đó.

Lời giải:

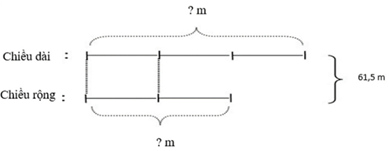
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 6)

Tổng số phần bằng nhau là:

2 + 3 = 5 (phần)

Chiều rộng hình chữ nhật là:

(61,5 : 5) × 2 = 12,3 (m)

Chiều dài hình chữ nhật là:

61,5 − 12,3 = 49,2 (m)

Diện tích hình chữ nhật là:

12,3 × 49,2 = 605,16 (m² )

Đáp số: 605,16 m²

Câu 26: Một mảnh vườn hình chữ nhật có chiều dài 20 m và chiều rộng 15 m. Người ta dành 20% diện tích mảnh vườn để trồng rau muống, 10% diện tích để trồng rau cải. Tính diện tích phần đất trồng rau muống, diện tích phần đất trồng rau cải.

Lời giải:

Diện tích mảnh đất hình chữ nhật là:

20 × 15 = 300 (m²)

Diện tích phần đất trồng rau muống là:

300 : 100 × 25 = 75 (m²)

Diện tích phần đất trồng rau cải là:

300 : 100 × 10 = 30 (m²)

Đáp số: 75 m² đất trồng rau muống

30 m² đất trồng rau cải

Câu 27: Người thợ may lấy ra một tấm vải lớn để cắt may 25 bộ quần áo cho công ty, mỗi chiếc ao may hết 500 cm vải, mỗi chiếc quần may hết 685 cm vải. Sau khi cắt xong thì tấm vải còn lại 5 dam. Vậy tấm vải ban đầu dài bao nhiêu cm?

Lời giải:

Đổi 5 dam = 5 000 cm

Số vải dùng để may 1 bộ quần áo là:

500 + 685 = 1 185 (cm)

Số vải dùng để may 25 bộ quần áo là:

1 185 × 25 = 29 625 (cm)

Tấm vải ban đầu dài là:

29 625 + 5 000 = 34 625 (cm)

Đáp số: 34 625 cm vải.

Câu 28: Một phân xưởng lắp ráp xe đạp, sáu tháng đầu năm phân xưởng đó lắp ráp được 36 900 xe đạp, sáu tháng cuối năm phân xưởng lắp ráp được nhiều hơn sáu tháng đầu năm 6 900 xe đạp. Vậy trong cả năm đó, trung bình mỗi tháng phân xưởng lắp ráp được số chiếc xe đạp là:

Lời giải:

Sáu tháng cuối năm lắp được số xe đạp là:

36 900 + 6 900 = 43 800 (xe đạp)

Cả năm phân xưởng đó lắp được số xe đạp là:

36 900 + 43 800 = 80 700 (xe đạp)

Vậy trong cả năm đó, trung bình mỗi tháng phân xưởng lắp ráp được số chiếc xe đạp là:

80 700 : 12 = 6 725 (xe đạp)

Đáp số: 6 725 xe đạp.

Câu 29: Cho hai điểm A(–1; –2) và B(–4; 3). Lập phương trình đường thẳng (d) đi qua A, B.

Lời giải:

Giả sử đường thẳng (d) có phương trình: y = ax + b.

Do đường thẳng (d) đi qua A, B nên ta có: $\{\begin{cases} - 2 = a . (- 1) + b \\ 3 = a . (- 4) + b \end{cases}$

$\Leftrightarrow \{\begin{cases} - a + b = - 2 \\ - 4 a + b = 3 \end{cases} \Leftrightarrow \{\begin{cases} - a + b = - 2 \\ 3 a = - 5 \end{cases} \Leftrightarrow \{\begin{cases} \frac{5}{3} + b = - 2 \\ a = - \frac{5}{3} \end{cases} \Leftrightarrow \{\begin{cases} b = - \frac{11}{3} \\ a = - \frac{5}{3} \end{cases}$

Vậy phương trình đường thẳng (d) là $y = - \frac{5}{3} x - \frac{11}{3}$ .

Câu 30: Cho đường tròn (O) và dây AB không đi qua tâm, gọi M là trung điểm AB. Qua M vẽ dây CD không trùng AB. Chứng minh rằng M không là trung điểm của CD.

Lời giải:

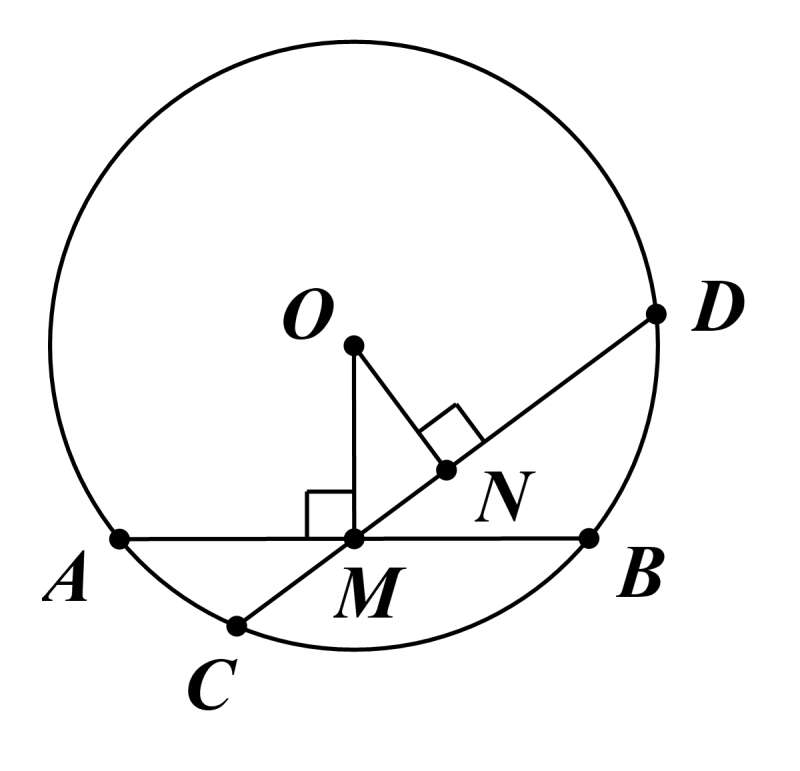
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 7)

Giả sử M là trung điểm của CD.

Suy ra OM ⊥ CD.

Mà OM ⊥ AB (do M là trung điểm AB).

Khi đó CD trùng với AB (mâu thuẫn với giả thiết).

Vậy M không là trung điểm của CD.

Câu 31: Khai triển biểu thức lượng giác cos4x theo cosx.

Lời giải:

Ta có cos4x = 2cos²2x – 1

= 2(2cos²x – 1)² – 1

= 2(4cos⁴x – 4cos²x + 1) – 1

= 8cos⁴x – 8cos²x + 2 – 1

= 8cos⁴x – 8cos²x + 1.

Vậy cos4x = 8cos⁴x – 8cos²x + 1.

Câu 32: Viết số thích hợp vào chỗ chấm:

a) 178 dm = … m … dm;

6789 cm = … m … dm … cm;

375 dam = … km … dam;

1987 m = … km … hm … m.

b) 245 dag = … kg … g;

318 g = … hg … dag … g;

408 kg = … tạ … kg;

8194 kg = … tấn … tạ … kg.

Lời giải:

a) 178 dm = 17 m 8 dm;

6789 cm = 67 m 8 dm 9 cm;

375 dam = 3 km 75 dam;

1987 m = 1 km 9 hm 87 m.

b) 245 dag = 2 kg 450 g;

318 g = 3 hg 1 dag 8 g;

408 kg = 4 tạ 8 kg;

8194 kg = 8 tấn 1 tạ 94 kg.

Câu 33: Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HM vuông góc với AB, HN vuông góc với AC. Chứng minh rằng tam giác AMN đồng dạng với tam giác ABC.

Lời giải:

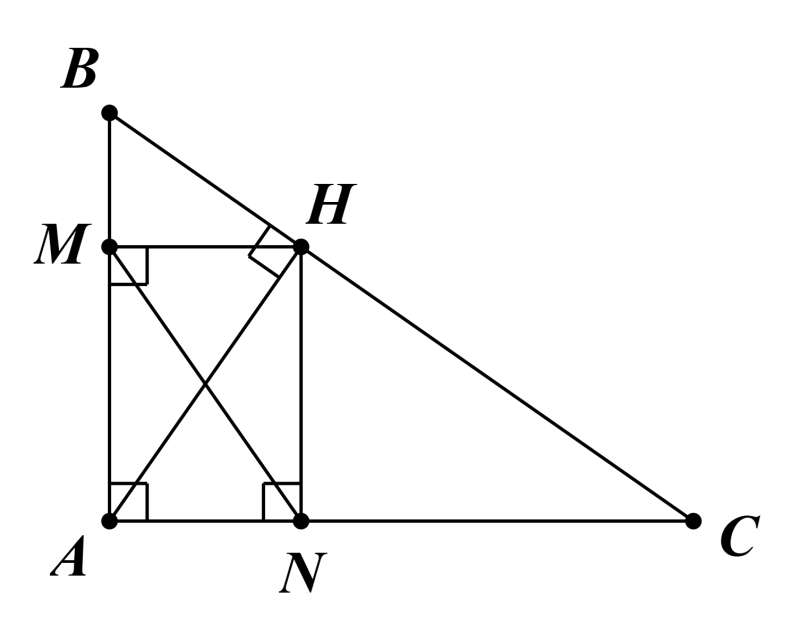
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 8)

∆ABH vuông tại H có HM là đường cao: AH² = AM.AB (hệ thức lượng trong tam giác vuông) (1)

∆ACH vuông tại H có HN là đường cao: AH² = AN.AC (hệ thức lượng trong tam giác vuông) (2)

Từ (1), (2), suy ra AM.AB = AN.AC.

Xét ∆AMN và ∆ABC, có:

$\hat{B A C} = 90 °$ ;

$\frac{A M}{A C} = \frac{A N}{A B}$ (do AM.AB = AN.AC).

Vậy $Δ A M N ∽ Δ A B C$ (c.g.c).

Câu 34: Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Gọi E, F là trung điểm CA, CB. Lấy M, N, I lần lượt thuộc các đoạn SA, SC, SB. Tìm giao tuyến của:

a) (SAE) và (SBF).

b) (BMN) và (SEF).

c) (CAI) và (BMN).

Lời giải:

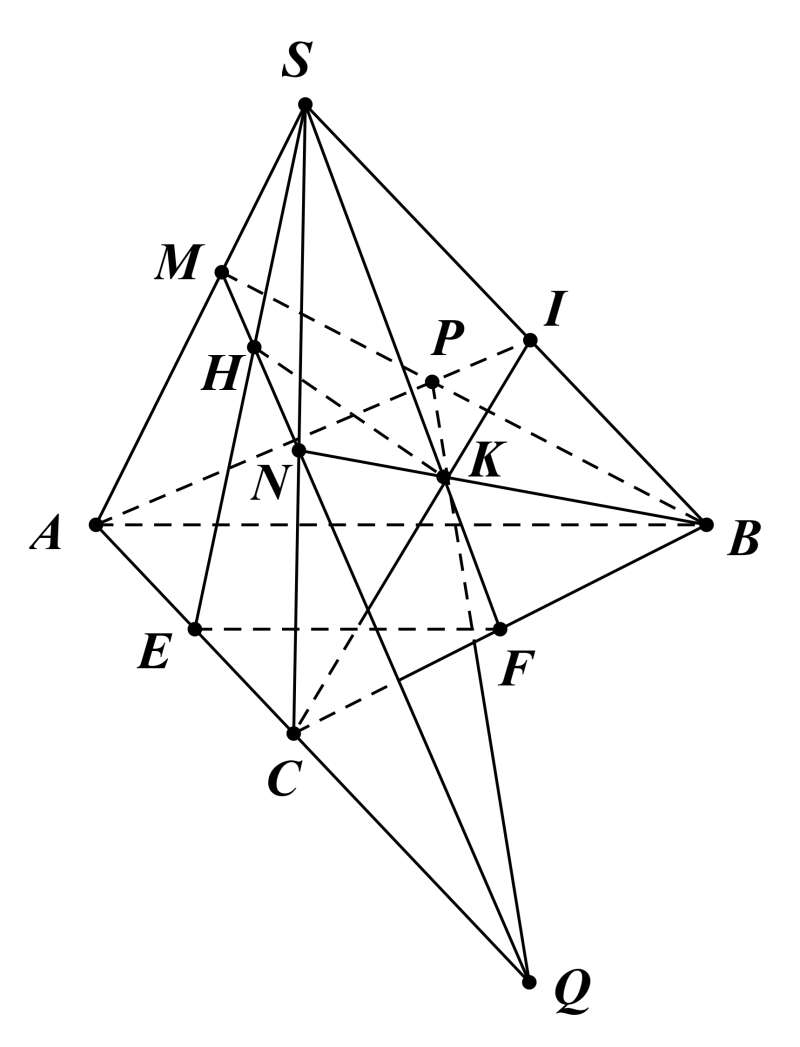
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 44) (ảnh 9)

a) Ta có S ∈ (SAE) ∩ (SBF) (1)

Trong (ABC): C = AE ∩ BF.

Suy ra C ∈ (SAE) ∩ (SBF) (2)

Từ (1), (2), suy ra SC = (SAE) ∩ (SBF).

b) Trong (SAC): gọi H = MN ∩ SE.

Suy ra H ∈ (BMN) ∩ (SEF) (3)

Trong (SBC): gọi K = BN ∩ SF.

Suy ra K ∈ (BMN) ∩ (SEF) (4)

Từ (3), (4), suy ra HK = (BMN) ∩ (SEF).

c) Trong (SAB): gọi P = AI ∩ BM.

Suy ra P ∈ (CAI) ∩ (BMN) (5)

Trong (SAC): gọi Q = AC ∩ MN.

Suy ra Q ∈ (CAI) ∩ (BMN) (6)

Từ (5), (6), suy ra PQ = (CAI) ∩ (BMN).

Câu 35: Có 45 m vải may được 9 bộ quần áo như nhau. Hỏi phải dùng bao nhiêu m vải đó để may được 7 bộ quần áo như thế?

Lời giải:

Để may 1 bộ quần áo cần dùng số mét vải là:

45 : 9 = 5 (m).

Để may được 7 bộ quần áo như thế cần dùng số mét vải là:

7 × 5 = 35 (m).

Đáp số: 35m.

Câu 36: Dấu hiệu chia hết cho 11 là gì? Có dấu hiệu chia hết cho 12 hay không?

Lời giải:

Dấu hiệu chia hết cho 11: Tổng các chữ số hàng lẻ – Tổng các chữ số hàng chẵn hoặc ngược lại chia hết cho 11.

Dấu hiệu chia hết cho 12: một số chia hết cho 12 khi số đó chia hết cho cả 3 và 4.

Câu 37: Tính giá trị biểu thức bằng cách hợp lí:

a) A = x5 – 100x4 + 100x3 – 100x2 + 100x – 9 tại x = 99.

b) B = x7 – 26x6 + 27x5 – 47x4 – 77x3 + 50 x 2 + x – 24 tại x = 25.

Lời giải:

Với x = 99, ta có: x + 1 = 99 + 1 = 100.

Ta có A = x⁵ – 100x⁴ + 100x³ – 100x² + 100x – 9

= x⁵ – (x + 1)x⁴ + (x + 1)x³ – (x + 1)x² + (x + 1)x – 9

= x⁵ – x⁵ – x⁴ + x⁴ + x³ – x³ – x² + x² + x – 9

= x – 9

= 99 – 9

= 90.

Vậy A = 90 khi x = 99.

b) Với x = 25, ta có: x + 1 = 26; x + 2 = 27; 2x – 3 = 7; 3x + 2 = 77 và 2x = 50.

B = x⁷ – 26x⁶ + 27x⁵ – 47x⁴ – 77x³ + 50x² + x – 24 tại x = 25.

= x⁷ – (x + 1)x⁶ + (x + 2)x⁵ – (2x – 3)x⁴ – (3x + 2)x³ + 2x.x² + x – 24

= x⁷ – x⁷ – x⁶ + x⁶ + 2x⁵ – 2x⁵ + 3x⁴ – 3x⁴ – 2x³ + 2x³ + x – 24

= x – 24

= 25 – 24

= 1.

Vậy B = 1 khi x = 25.

Câu 38: Hỏi có bao nhiêu phân số thập phân khác 0 mà tổng của mẫu số và tử số là số lẻ nhỏ nhất có tám chữ số?

Lời giải:

Gọi phân số thỏa mãn yêu cầu bài toán có dạng là $\frac{a}{b}$ (a, b ∈ ℕ, b ≠ 0).

Do phân số cần tìm là phân số thập phân nên b ∈ {10; 100; 1000; …}.

Theo đề, ta có tổng của mẫu số và tử số là số lẻ nhỏ nhất có tám chữ số.

Suy ra tổng của mẫu số và tử số bằng 10000001.

Khi đó 0 < a, b < 10000001.

Suy ra b ∈ {10; 100; 1000; 10000; 100000; 1000000; 10000000}.

Với b = 10, ta có: a = 10000001 – 10 = 9999991.

Với b = 100, ta có: a = 10000001 – 100 = 9999901.

Với b = 1000, ta có: a = 10000001 – 1000 = 9999001.

Với b = 10000, ta có: a = 10000001 – 10000 = 9990001.

Với b = 100000, ta có: a = 10000001 – 100000 = 9900001.

Với b = 1000000, ta có: a = 10000001 – 1000000 = 9000001.

Với b = 10000000, ta có: a = 10000001 – 10000000 = 1.

Vậy có 7 chữ số thập phân thỏa mãn yêu cầu bài toán.

Câu 39: Tính (tính hợp lí nếu có thể):

–3752 – (29 – 3632) – 51.

Lời giải:

Ta có:

–3752 – (29 – 3632) – 51

= –3752 – 29 + 3632 – 51

= (–3752 + 3632) – (29 + 51)

= –120 – 80

= – 200.

Câu 40: Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 5050.

Lời giải:

Ta có (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 5050.

⇔ (x + x + x + … + x) + (1 + 2 + 3 + … + 100) = 5050.

⇔ 100x + (1 + 2 + 3 + … + 100) = 5050 (1)

Xét dãy số: 1; 2; 3; …; 100.

Số các số hạng của dãy số trên là: (100 – 1) : 1 + 1 = 100 (số hạng).

Tổng của dãy số trên là: (100 + 1) . 100 : 2 = 5050.

Từ (1), ta có: 100x + 5050 = 5050.

⇔ 100x = 0.

⇔ x = 0 : 100 = 0.

Vậy x = 0.

Câu 41: Tìm x, biết: (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 6050.

Lời giải:

Ta có (x + 1) + (x + 2) + (x + 3) + … + (x + 100) = 6050.

⇔ (x + x + x + … + x) + (1 + 2 + 3 + … + 100) = 6050.

⇔ 100x + (1 + 2 + 3 + … + 100) = 6050 (1)

Xét dãy số: 1; 2; 3; …; 100.

Số các số hạng của dãy số trên là: (100 – 1) : 1 + 1 = 100 (số hạng).

Tổng của dãy số trên là: (100 + 1) . 100 : 2 = 5050.

Từ (1), ta có: 100x + 5050 = 6050.

⇔ 100x = 1000.

⇔ x = 1000 : 100 = 10.

Vậy x = 10.

Câu 42: Giải phương trình: (x + 1)³ – (x – 1)(x² + x + 1) – 2 = 0.

Lời giải:

Ta có (x + 1)³ – (x – 1)(x² + x + 1) – 2 = 0.

⇔ x³ + 3x² + 3x + 1 – (x³ – 1) – 2 = 0.

⇔ 3x² + 3x = 0.

⇔ 3x(x + 1) = 0.

$\Leftrightarrow [\begin{array}{l} x = 0 \\ x + 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 1 \end{array}$

Vậy tập nghiệm của phương trình đã cho là: S = {0; –1}.

Câu 43: Phân tích đa thức thành nhân tử: x⁵ – x⁴ + x³ – x².

Lời giải:

Ta có x⁵ – x⁴ + x³ – x² = x⁴.(x – 1) + x².(x – 1)

= x².(x – 1)(x² + 1).

Câu 44: Phân tích đa thức thành nhân tử: x⁵ – x⁴ – x³ – x² – x – 2.

Lời giải:

Ta có x⁵ – x⁴ – x³ – x² – x – 2 = x⁵ – 2x⁴ + x⁴ – 2x³ + x³ – 2x² + x² – 2x + x – 2

= x⁴.(x – 2) + x³.(x – 2) + x².(x – 2) + x.(x – 2) + (x – 2)

= (x – 2).(x⁴ + x³ + x² + x + 1).

Câu 45: Tổng của hai số là 0,6. Thương của hai số cũng bằng 0,6. Tìm hai số đó.

Lời giải:

Vì thương của hai số là 0,6 hay $0,6 = \frac{6}{10} = \frac{3}{5}$ nên tỉ số của hai số đó là $\frac{3}{5}$ .

Số bé là: 0,6 : (3 + 5) x 3 = 0,225.

Số lớn là: 0,6 – 0,225 = 0,375.

Đáp số: Số bé là: 0,225;

Số lớn là: 0,375.

Câu 46: Tìm y biết:

y × 1 + y × 1,5 + y × 2 + y × 2,5 + y × 3 + … + y × 5 = 94,5.

Lời giải:

Ta có:

y × 1 + y × 1,5 + y × 2 + y × 2,5 + y × 3 + … + y × 5 = 94,5.

y × (1 + 1,5 + 2 + 2,5 + 3 + 3,5 + 4 + 4,5 + 5) = 94,5

y × [(1 + 2 + 3 + 4 + 5) + (1,5 + 2,5 + 3,5 + 4,5)] = 94,5

y × (15 + 12) = 94,5

y × 27 = 94,5

y = 94,5 : 27

y = 3,5.

Vậy y = 3,5.

Câu 47: Cho đa giác đều gồm 2023 cạnh. Người ta sơn các đỉnh của đa giác bằng hai màu xanh và đỏ. Chứng minh ràng tồn tại ba đỉnh được sơn cùng một màu tạo thành một đa giác cân.

Lời giải:

Ta có đa giác 2023 cạnh nên có 2023 đỉnh.

Do đó phải tồn tại 2 đỉnh kề nhau là P và Q đc sơn bởi cùng 1 màu – màu đỏ (Theo nguyên tắc dirichlet)

Vì đa giác đã cho là đa giác đều có số đỉnh lẻ nên phải tồn tại 1 đỉnh nào đó nằm trên đường trung trực của đoạn thẳng PQ. Giả sử đỉnh đó là A.

– Nếu A tô màu đỏ thì ta có tam giác APQ là tam giác cân có 3 đỉnh A, P, Q đc tô cùng màu đỏ.

– Nếu A tô màu xanh. Lúc đó gọi B và C là các đỉnh khác nhau của đa giác kề vs P và Q.

• Nếu cả 2 đỉnh B và C đc tô màu xanh thì tam giác ABC cân và có 3 đỉnh cùng tô màu xanh.

• Nếu ngược lại, 1 trong 2 đỉnh B và C đc tô màu đỏ thì tam giác BPQ hoặc tam giác CPQ là tam giác cân có 3 đỉnh đc tô màu đỏ.

Vậy ta có điều phải chứng minh.

Câu 48: Bác Tư trồng lúa mì trên hai mảnh đất, cuối năm thu được 5795 kg. Mảnh đất thứ hai thu kém mảnh đất thứ nhất 1125 kg. Hỏi mảnh đất thứ hai thu được bao nhiêu yến lúa mì?

Lời giải:

Số kg lúa mì mảnh đất thứ hai thu được là: (5795 – 1125) : 2 = 2335 (kg).

Đổi: 2335 kg = 233,5 yến.

Đáp số: 233,5 yến lúa mì.

Câu 49: Đường gấp khúc ABCD có AB bằng 15 cm, biết đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3 cm. Tính độ dài đoạn thẳng DC.

Lời giải:

Ta thấy đường gấp khúc ABC và đường gấp khúc BCD có chung đoạn BC.

Mà đường gấp khúc ABC dài hơn đường gấp khúc BCD là 3cm.

Nên đoạn thẳng AB dài hơn đoạn thẳng CD là 3 cm.

Độ dài đoạn thẳng CD là: 15 – 3 = 12 (cm).

Đáp số: 12 cm.

Câu 50: Cho các số a, b, c. Biết a là số có một chữ số, b là số có hai chữ số, c là số có ba chữ số và trung bình cộng của ba số đó là 369. Tìm số c.

Lời giải:

Vì trung bình cộng của ba số đó là 369 nên a + b + c = 369.3 = 1107.

Ta có:

⦁ a là số có một chữ số. Suy ra a lớn nhất là 9;

⦁ b là số có hai chữ số. Suy ra b lớn nhất là 99;

⦁ c là số có ba chữ số. Suy ra c lớn nhất là 999.

Mà 9 + 99 + 999 = 1107.

Do đó a = 9; b = 99; c = 999.

Vậy c = 999.

Từ khóa :

Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

227

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236