Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68)

Ngọc Nguyễn Ngày: 23-09-2023 Tổng hợp kiến thức

345

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68)

Câu 1: Cho hàm số f(x) = mx + m – 1. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = 0 có nghiệm thuộc (3; 4).

Lời giải:

Xét phương trình f(x) = 0 ⇔ mx + m – 1 = 0.

Trường hợp 1: m = 0.

Khi đó phương trình f(x) = 0 ⇔ 0.x = 1 (vô nghiệm).

Vì vậy ta loại m = 0.

Trường hợp 2: m ≠ 0.

Phương trình $f (x) = 0 \Leftrightarrow x = \frac{1 - m}{m}$ .

Phương trình f(x) = 0 có nghiệm thuộc (3; 4).

$\Leftrightarrow \{\begin{cases} \frac{1 - m}{m} > 3 \\ \frac{1 - m}{m} < 4 \end{cases} \Leftrightarrow \{\begin{cases} \frac{1 - 4 m}{m} > 0 \\ \frac{1 - 5 m}{m} < 0 \end{cases} \Leftrightarrow \{\begin{cases} 0 < m < \frac{1}{4} \\ [\begin{array}{l} m < 0 \\ m > \frac{1}{5} \end{array} \end{cases} \Leftrightarrow \frac{1}{5} < m < \frac{1}{4}$

So với điều kiện m ≠ 0, ta nhận $\frac{1}{5} < m < \frac{1}{4}$ .

Vậy $\frac{1}{5} < m < \frac{1}{4}$ thỏa mãn yêu cầu bài toán.

Câu 2: Một cửa hàng giảm giá 10% so với giá bán bình thường nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm so với giá vốn?

Lời giải:

Do hạ giá 10% nên giá bán mới bằng 90% giá bình thường.

Coi giá vốn là 100% thì giá bán mới bằng 108% giá vốn.

Như vậy $\frac{108}{100}$ (giá vốn) = $\frac{90}{100}$ (giá bình thường).

Giá bình thường so với giá vốn là:

$\frac{108}{100} : \frac{90}{100} = \frac{6}{5} = 120 %$ .

Nếu không giảm giá thị cửa hàng lãi là:

120% – 100% = 20%.

Đáp số: 20%.

Câu 3: Tìm x, y ∈ ℤ, biết: (5x + 1)(y – 1) = 4.

Lời giải:

Vì x, y ∈ ℤ và (5x + 1)(y – 1) = 4 nên ta có bảng sau:

5x + 1	–4	–2	–1	1	2	4
y – 1	–1	–2	–4	4	2	1
x	–1	$- \frac{3}{5}$	$- \frac{2}{5}$	0	$\frac{1}{5}$	$\frac{3}{5}$
y	0	–1	–3	5	3	2
	Nhận	Loại	Loại	Nhận	Loại	Loại

Vậy (x; y) ∈ {(–1; 0), (0; 5)}.

Câu 4: Thực hiện phép tính: C = (x – 2)(x² + 2x + 4) – x²(x + 2).

Lời giải:

C = (x – 2)(x² + 2x + 4) – x²(x + 2).

= x³ – 2³ – x³ – 2x².

= –2x² – 8.

Câu 5: Cách xác định cạnh kề, cạnh đối, cạnh huyền trong tam giác vuông.

Lời giải:

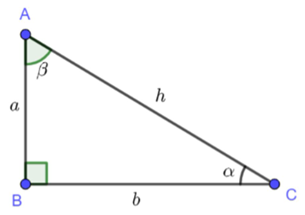
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 1)

Giả sử ta có tam giác vuông như hình vẽ.

Với góc α < 90°, ta có b là cạnh kề, a là cạnh đối, h là cạnh huyền.

Với góc β < 90°, ta có a là cạnh kề, b là cạnh đối, h là cạnh huyền.

Tóm lại:

Cạnh huyền là cạnh đối diện góc vuông.

Cạnh kề là cạnh góc vuông kề với góc đó.

Cạnh đối là cạnh góc vuông đối diện với góc đó.

Câu 6: a) Viết phương trình đường thẳng biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 4 và cắt trục hoành tại điểm có hoành độ bằng –3.

b) Viết phương trình đường thẳng (d) biết (d) có hệ số góc là –2 và đi qua điểm A(–1; 5).

Lời giải:

a) Phương trình đường thẳng cần tìm có dạng: y = ax + b (a ≠ 0).

Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 4 nên 4 = a.0 + b ⇔ b = 4.

Vì đường thẳng cắt trục hoành tại điểm có hoành độ bằng –3 nên 0 = –3a + b.

⇔ –3a + 4 = 0.

$\Leftrightarrow a = \frac{4}{3}$ (nhận).

Vậy phương trình đường thẳng cần tìm là $y = \frac{4}{3} x + 4$ .

b) Phương trình đường thẳng (d) cần tìm có dạng: y = ax + b (a ≠ 0).

Đường thẳng (d) có hệ số góc là –2 nên ta có a = –2.

Vì (d) đi qua điểm A(–1; 5) nên 5 = a.(–1) + b.

⇔ 5 = 2 + b.

⇔ b = 3.

Vậy phương trình đường thẳng (d): y = –2x + 3.

Câu 7: Cho hàm số y = (m – 1)x + m (1) (với m là tham số, m ≠ 0).

a) Tìm m để đồ thị hàm số (1) đi qua điểm M(1; 3).

b) Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 4. Vẽ đồ thị hàm số với m tìm được.

Lời giải:

a) Vì đồ thị hàm số (1) đi qua điểm M(1; 3) nên 3 = (m – 1).1 + m.

⇔ 3 = m – 1 + m.

⇔ m = 1.

Vậy m = 1 thỏa mãn yêu cầu bài toán.

b) Vì đường thẳng cắt trục tung tại điểm có tung độ bằng 4 nên 4 = (m – 1).0 + m.

⇔ m = 4.

Vậy m = 4 thỏa mãn yêu cầu bài toán.

Với m = 4, ta có y = 3x + 4.

Bảng giá trị:

x	–2	–1	0
y	–2	1	4

Đồ thị hàm số y = 3x + 4:

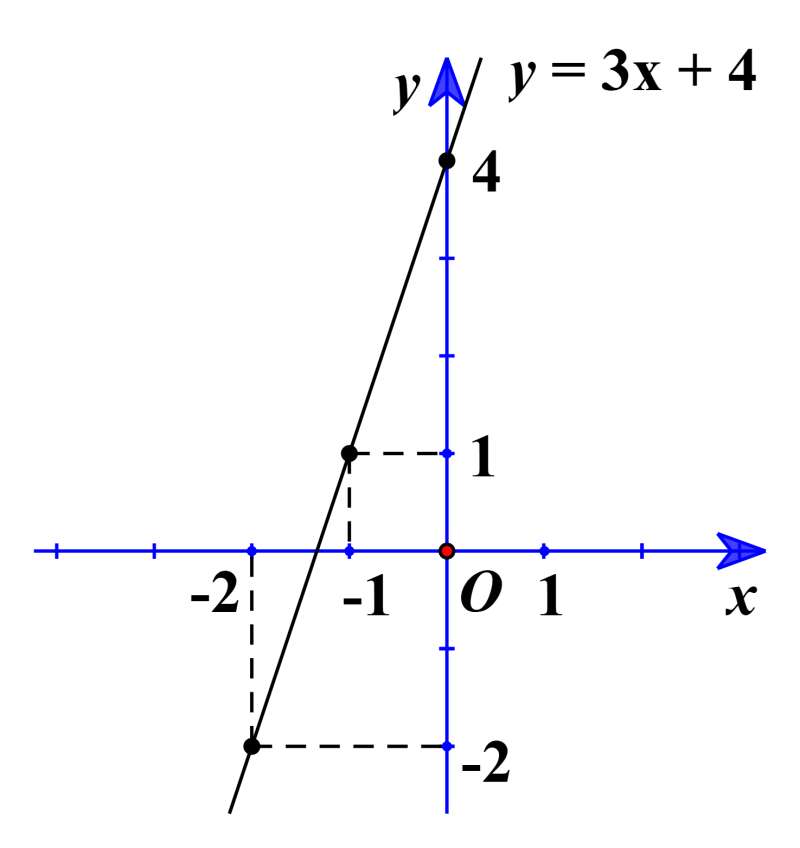
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 2)

Câu 8: Tìm dư trong phép chia đa thức f(x) = 1 + x² + x⁴ + x⁶ + ... + x¹⁰⁰ cho x + 1.

Lời giải:

Theo định lí Bezout thì dư của phép chia đa thức f(x) = 1 + x² + x⁴ + x⁶ + ... + x¹⁰⁰ cho x + 1 là f(–1).

Ta có f(–1) = 1 + (–1)² + (–1)⁴ + (–1)⁶ + ... + (–1)¹⁰⁰ = 1 + 1 + 1 + 1 + ... + 1 = 51.

Vậy dư trong phép chia đa thức f(x) = 1 + x² + x⁴ + x⁶ + ... + x¹⁰⁰ cho x + 1 là 51.

Câu 9: Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.

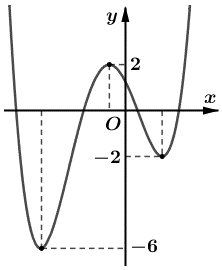
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 3)

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g(x) = |f(x) – m + 2018| có 7 điểm cực trị?

Lời giải:

Quan sát đồ thị, ta thấy hàm số y = f(x) có 3 điểm cực trị.

Do đó để hàm số y = |f(x) – m + 2018| có 7 điểm cực trị thì đồ thị hàm số y = f(x) cắt đường thẳng y = m – 2018 tại 7 – 3 = 4 điểm phân biệt khác 3 điểm cực trị của hàm số y = f(x).

⇔ –2 < m – 2018 < 2.

⇔ 2016 < m < 2020.

Mà m ∈ ℤ.

Suy ra m ∈ {2017; 2018; 2019}.

Vậy có 3 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.

Câu 10: Cho tam giác ABC và đường trung tuyến AM. Chứng minh S_AMB = S_AMC.

Lời giải:

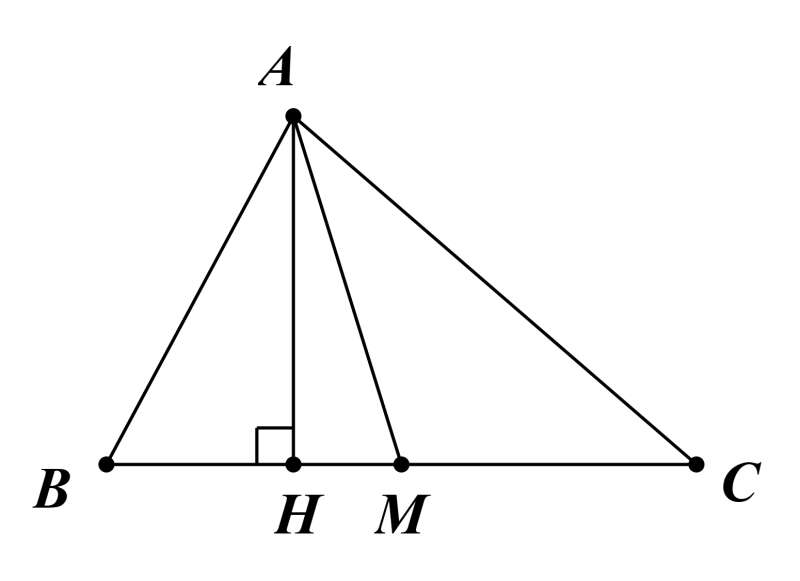
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 4)

Kẻ đường cao AH của tam giác ABC.

Ta có $S_{A M B} = \frac{1}{2} A H . M B$ và $S_{A M C} = \frac{1}{2} A H . M C$ .

Mà MB = MC (do AM là đường trung tuyến của tam giác ABC).

Vậy S_AMB = S_AMC (điều phải chứng minh).

Câu 11: Từ các chữ số 0; 1; 2; 3; 4; 5; 6, có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau và phải có mặt chữ số 5?

Lời giải:

Gọi chữ số cần lập là $\bar{a b c d e}$ .

Trường hợp 1: có mặt chữ số 0.

Chọn 3 chữ số còn lại (ngoài hai số 0 và 5) thì có $C_{5}^{3} = 10$ cách.

Hoán vị 5 chữ số và loại đi trường hợp a = 0 thì có 5! – 4! cách.

Suy ra ta có tất cả 10.(5! – 4!) = 960 số thỏa mãn trường hợp 1.

Trường hợp 2: không có mặt chữ số 0.

Chọn 4 chữ số còn lại thì có $C_{5}^{4} = 5$ cách.

Hoán vị 5 chữ số thì có 5! cách.

Suy ra ta có tất cả 5.5! = 600 số thỏa mãn trường hợp 2.

Vậy ta có tất cả 960 + 600 = 1560 số thỏa mãn yêu cầu bài toán.

Câu 12: Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không đổi. Tính diện tích hình chữ nhật.

Lời giải:

Ta có nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không đổi.

Khi đó chiều rộng thành chiều dài và chiều dài thành chiều rộng. Chiều dài hơn chiều rộng 5 m.

Chiều dài hình chữ nhật là:

(99 + 5) : 2 = 52 (m).

Chiều rộng hình chữ nhật là:

(99 – 5) : 2 = 47 (m).

Diện tích hình chữ nhật là:

52 × 47 = 2444 (m²).

Đáp số: 2444 m².

Câu 13: Hai người xài youtube mất 2 phút để đăng 2 đoạn video. Vậy cần bao nhiêu người để đăng được 18 clip trong vòng 6 phút?

A. 3.

B. 6.

C. 12.

Lời giải:

Đáp án đúng là: B

Vì 2 người trong 6 phút sẽ đăng được 6 clip nên sẽ cần 3 nhóm 2 người là 6 người để đăng được 18 clip trong vòng 6 phút.

Do đó ta chọn phương án B.

Câu 14: Biết đồ thị hàm số y = ax + 5 đi qua điểm M(2; –3) thì hệ số góc bằng bao nhiêu?

Lời giải:

Đường thẳng y = ax + 5 (d) đi qua M(2; –3) nên ta thay x = 2; y = –3 vào (d) ta được:

2a + 5 = − 3

⇔ 2a = −3 – 5 = −8

⇔ a= −4

Vậy hệ số góc bằng –4.

Câu 15: Đồ thị hàm số y = –5x không đi qua điểm:

A. M(1; 5);

B. N(–2; 10);

C. P(–1; 5);

D. Q(2; –10).

Lời giải:

Đáp án đúng là: A

Với M(1; 5), thay x = 1 và y = 5 vào y = –5x ta được:

5 = –5.1 ⇔ 5 = –5 (vô lí).

Do đó đồ thị hàm số y = –5x không đi qua điểm M(1; 5).

Câu 16: Một mảnh đất hình chữ nhật có chiều dài là 36 m, chiều rộng bằng $\frac{1}{4}$ chiều dài. Hãy tính diện tích mảnh đất đó?

Lời giải:

Chiều rộng mảnh đất đó là:

$36 \times \frac{1}{4} = 9$ (m)

Diện tích mảnh đất đó là:

36 × 9 = 324 (m²)

Đáp số: 324 m².

Câu 17: Tìm số nguyên x, y, biết: (x – 3)(y + 1) = 15.

Lời giải:

Vì x, y ∈ ℤ và (x – 3)(y + 1) = 15 nên ta có bảng sau:

x – 3	–15	–5	–3	–1	1	3	5	15
y + 1	–1	–3	–5	–15	15	5	3	1
x	–12	–2	0	2	4	6	8	18
y	–2	–4	–6	–16	14	4	2	0
	Nhận	Nhận	Nhận	Nhận	Nhận	Nhận	Nhận	Nhận

Vậy (x; y) ∈ {(–12; –2), (–2; –4), (0; –6), (2; –16), (4; 14), (6; 4), (8; 2), (18; 0)}.

Câu 18: Tìm số giao điểm của parabol y = –x² – 3x – 1 và đường thẳng y = x + 3.

Lời giải:

Phương trình hoành độ giao điểm: –x² – 3x – 1 = x + 3.

⇔ x² + 4x + 4 = 0.

⇔ (x + 2)² = 0.

⇔ x = –2.

Với x = –2, ta có y = 1.

Suy ra tọa độ giao điểm A(–2; 1).

Vậy số giao điểm của parabol y = –x² – 3x – 1 và đường thẳng y = x + 3 là 1.

Câu 19: Cho hai số, biết số bé bằng $\frac{9}{11}$ số lớn và nếu lấy số lớn trừ đi số bé và cộng với hiệu của chúng thì được kết quả là 12. Gọi số lớn là A. So sánh A với 30.

Lời giải:

Ta có: Số lớn – Số bé + Hiệu = 2 × Hiệu = 12.

Hiệu số phần bằng nhau là: 11 – 9 = 2 (phần).

Hiệu của hai số đó là: 12 : 2 = 6.

Số lớn là: 6 : 2 × 11 = 33.

Vì 33 > 30 nên A > 30.

Vậy A > 30.

Câu 20: Cho hàm số y = ax² + bx + c có đồ thị như hình vẽ bên.

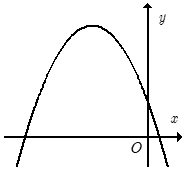
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 5)

Khẳng định nào sau đây đúng?

A. a > 0, b < 0, c > 0.

B. a < 0, b < 0, c < 0.

C. a < 0, b > 0, c > 0.

D. a < 0, b < 0, c > 0.

Lời giải:

Đáp án đúng là: D

Bề lõm của đồ thị hướng xuống nên a < 0.

Hoành độ đỉnh parabol $x = \frac{- b}{2 a} < 0$ .

Mà a < 0.

Suy ra –b > 0.

Do đó b < 0.

Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.

Vậy a < 0, b < 0, c > 0.

Do đó ta chọn phương án D.

Câu 21: Cho hàm số y = ax² + bx + c có đồ thị như hình bên.

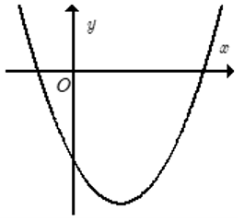
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 6)

Khẳng định nào sau đây đúng?

A. a > 0, b < 0, c < 0.

B. a > 0, b < 0, c > 0.

C. a > 0, b > 0, c > 0.

D. a < 0, b < 0, c > 0.

Lời giải:

Đáp án đúng là: A

Bề lõm của đồ thị hướng lên nên a > 0.

Hoành độ đỉnh parabol $x = \frac{- b}{2 a} > 0$ .

Mà a > 0.

Suy ra –b > 0.

Do đó b < 0.

Parabol cắt trục tung tại điểm có tung độ âm nên c < 0.

Vậy a > 0, b < 0, c < 0.

Do đó ta chọn phương án A.

Câu 22: Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần

A. 35 280 số;

B. 40 320 số;

C. 5 880 số;

D. 840 số.

Lời giải:

Đáp án đúng là: C

Do chữ số 1 có mặt 3 lần nên ta coi như tìm các số thỏa mãn đề bài được tạo nên từ 8 số 0, 1, 1, 1, 2, 3, 4, 5

Chọn số cho ô đầu tiên có 7 cách

Chọn số cho ô thứ hai có 7 cách

…

Chọn số cho ô thứ 88 có 1 cách

Suy ra có 7 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 7 . 7! cách xếp 8 chữ số 0, 1, 1, 1, 2, 3, 4, 5 vào 8 ô

Mặt khác chữ số 1 lặp lại 3 lần nên số cách xếp là

$\frac{7.7!}{3!} = 5880$ số

Vậy ta chọn đáp án C.

Câu 23: Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ

A. 6;

B. 72;

C. 720;

D. 144.

Lời giải:

Đáp án đúng là: B

Chọn vị trí cho hai nhóm 3 nam và 3 nữ có 2 cách chọn (1 nhóm ở vị trí chẵn và nhóm còn lại ở vị trí lẻ)

Xếp 3 nam có: 3 . 2 . 1 cách xếp

Xếp 3 nữ có: 3 . 2 . 1 cách xếp

Vậy có 2 . (3 . 2 . 1)² =72 cách xếp

Vậy ta chọn đáp án B.

Câu 24: Diện tích hình tam giác là 25,3 cm², chiều cao là 5,5 cm. Tính độ dài đáy của hình tam giác đó.

Lời giải:

Độ dài đáy của hình tam giác đó là:

25,3 × 2 : 5,5 = 9,2 (cm)

Vậy độ dài đáy là 9,2 cm.

Câu 25: Tìm số có 3 chữ số abc sao cho $\frac{a b c}{a + b + c}$ lớn nhất.

Lời giải:

Để $\frac{a b c}{a + b + c}$ lớn nhất thì abc lớn nhất và a + b + c nhỏ nhất

Vì a + b + c nhỏ nhất nên a + b + c = 3

Suy ra abc = 111

Vậy số cần tìm là 111.

Câu 26: Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.

Lời giải:

Vì ƯCLN(a, b) = 4

Nên a = 4m, b = 4n (m, n ∈ ℕ*)

Ta có: a + b = 48

Nên 4m + 4n = 48

Hay m + n = 12

Mà (m, n) = 1

Suy ra (m; n) ∈ {(1; 11); (11; 1); (5; 7); (7; 5)}

Do đó (a; b) ∈ {(4; 44); (44; 4); (20; 28); (28; 20)}.

Vậy hai số cần tìm là 4 và 44 hoặc 20 và 28.

Câu 27: Cho đường thẳng d: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là:

A. 9;

B. 18;

C. 12;

D. 6.

Lời giải:

Đáp án đúng là: A

Đường thẳng d cắt Ox tại A nên y_A = 0

Khi đó 2x_A + 6 = 0 hay x_A = –3

Do đó A(–3; 0). Suy ra OA = 3

Đường thẳng d cắt Oy tại B nên x_B = 0

Khi đó 2 . 0 + 6 = y_B hay y_B = 6

Do đó B(0; 6). Suy ra OB = 6

Vì tam giác AOB vuông tại O nên

$S_{A O B} = \frac{1}{2} O A . O B = \frac{1}{2} .3.6 = 9$

Vậy ta chọn đáp án A.

Câu 28: Số nào khác tính chất với các số còn lại: 9678, 4572, 5261, 5133, 3527, 6895, 7768.

Lời giải:

Trong 2 số đầu của mỗi chữ số có tổng 2 số cuối là:

9 + 6 = 7 + 8

4 + 5 = 7 + 2

5 + 2 = 6 + 1

5 + 1 = 3 + 3

6 + 8 = 9 + 5

7 + 7 = 6 + 8

Nhưng có một số khác biệt:

3 + 5 ≠ 7 + 2

Suy ra số này sai quy luật

Vậy số khác biệt là 3527.

Câu 29: Một khu vườn hình chữ nhật có diện tích 3600 m² chiều rộng 40 m, cửa ra vào của khu vườn rộng 5 m. Người ta muốn làm hàng rào xung quanh vườn bằng 2 tầng dây thép gai. Hỏi cần phải dùng bao nhiêu mét thép gai để làm hàng rào?

Lời giải:

Chiều dài khu vườn là:

3600 : 40 = 90 (m)

Chu vi khu vườn là:

(90 + 40) × 2 = 260 (m)

Cần phải dùng số mét thép gai để làm hàng rào là:

(260 – 5 ) × 2 = 510 (m)

Vậy cần dùng 510 m thép gai để làm hàng rào.

Câu 30: Cho một hình chữ nhật và một hình thoi (như hình vẽ), đường chéo EK và FH của hình thoi lần lượt bằng chiều rộng, chiều dài của hình chữ nhật ABCD, biết hình chữ nhật ABCD có chiều dài gấp đôi chiều rộng và có diện tích bằng 32 m². Tính diện tích hình thoi EFKH.

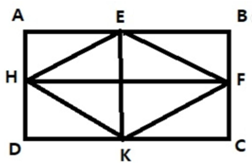
Lời giải:

Gọi chiều rộng hình chữ nhật là x (m)

Suy ra chiều dài hình chữ nhật là 2x (m)

Diện tích hình chữ nhật là:

x × 2x = 2x² = 32 (m²)

Suy ra x² = 16, do đó x = 4 (m)

Do đó EK = 4 và HF = 8

Diện tích hình thoi EFKH là:

$S = \frac{E K . H F}{2} = \frac{4.8}{2} = 16$ (m²).

Câu 31: Trong các hình sau : hình vuông, hình bình hành, hình chữ nhật; hình thang cân. Những hình nào có hai đường chéo bằng nhau?

A. Hình vuông, hình chữ nhật, hình thang cân;

B. Hình vuông, hình chữ nhật, hình bình hành;

C. Hình vuông, hình bình hành, hình thang cân;

D. Hình bình hành, hình chữ nhật, hình thang cân.

Lời giải:

Đáp án đúng là: A

Các hình có đường chéo bằng nhau là: Hình vuông, hình chữ nhật, hình thang cân

Vậy ta chọn đáp án A.

Câu 32: Tính diện tích tam giác vuông cân biết cạnh huyền 4 cm.

Lời giải:

Gọi a (cm) là độ dài cạnh góc vuông (a > 0)

Áp dụng định lý Pytago ta có: a² + a² = 4²

$\Rightarrow a = 2 \sqrt{2}$

$\Rightarrow S = \frac{1}{2} a^{2} = 4 (c m^{2})$ .

Vậy diện tích tam giác vuông cân biết cạnh huyền 4 cm là 4 cm².

Câu 33: Tìm số nguyên x, biết: (–14 ) + x – 7 = –10.

Lời giải:

(–14) + x – 7 = –10

(–14) + x = (–10) + 7

(–14) + x = –3

x = –3 – (–14)

x = –3 + 14

x = 11

Vậy x = 11.

Câu 34: Tìm x biết x² + 2 là bội của x + 2.

Lời giải:

Ta có : x² + 2 là bội của x + 2

Suy ra x² + 2 ⋮ x + 2

Ta có x² + 2 = x² – 4 + 6 = (x – 2)(x + 2) + 6

Mà (x – 2)(x + 2) ⋮ (x + 2)

Nên 6 ⋮ x + 2

Suy ra x + 2 ∈ Ư(6) ={1; –1; 2; –2; 3; –3; 6; –6}

Do đó x ∈ {–1; –3; 0; –4; 1; –5; 4; –8}

Vậy x ∈ {–1; –3; 0; –4; 1; –5; 4; –8}.

Câu 35: Tính nhanh :

a) 55 + 56 + 57 + 58 – 35 – 36 – 37 – 38.

b) (461 – 78 + 40) – (461 – 78 – 60).

c) –323 + 874 – (874 – 324 – 241).

Lời giải:

a) 55 + 56 + 57 + 58 – 35 – 36 – 37 – 38

= (55 – 35) + (56 – 36) + (57 – 37) + (58 – 38)

= 20 + 20 + 20 + 20

= 80.

b) (461 – 78 + 40) – (461 – 78 – 60)

= 461 – 78 + 40 – 461 + 78 + 60

= (461 – 461) + (78 – 78) + (40 + 60)

= 0 + 0 + 100

= 100.

c) –323 + 874 – (874 – 324 – 241)

= –323 + 874 – 874 + 324 + 241

= (–323 + 324) + (874 – 874) + 241

= 1 + 0 + 241

= 242.

Câu 36: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I

a) Chứng minh AD song song BM và tứ giác ADBM là hình thoi.

b) Gọi E là giao điểm của AB và DC. Chứng minh AE = EM.

Lời giải:

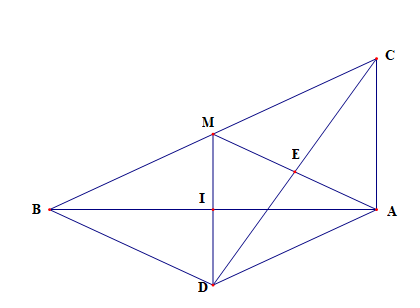
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 9)

a) Xét tứ giác ADBM có I là trung điểm của hai đường chéo MD và AB

Suy ra ADBM là hình bình hành

Lại có AB ⊥ MD (do D là điểm đối xứng của M qua I)

Do đó ADBM là hình thoi

Suy ra AD // BM

b) Vì ADBM là hình thoi nên AM // BD

Ta có: CA ⊥ AB và MI ⊥ AB

Suy ra CA // MI (quan hệ từ vuông góc đến song song)

Xét tứ giác ADMC có CM // AD, MD // AC

Suy ra ADMC là hình bình hành

Mà AM cắt CD tại trung điểm E nên AE = EM

Vậy AE = EM.

Câu 37: Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:

A. SA = 3SD.

B. SA = 2SD.

C. SA = SD.

D. 2SA = 3SD.

Lời giải:

Đáp án đúng là: B

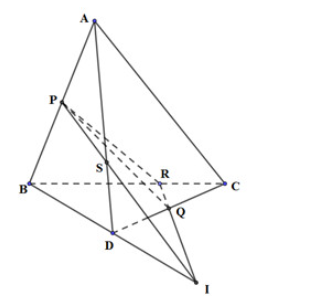
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 10)

Trong (BCD) gọi I là giao điểm của RQ và BD

Trong (ABD) gọi S là giao điểm của AD và IP

Khi đó, S = AD ∩ (PQR)

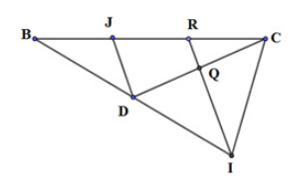
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 68) (ảnh 11)

Gọi J là trung điểm của BR. DO R nằm trên cạnh BC sao cho BR = 2RC

Suy ra BJ = JR = RC

Xét tam giác JCD có R, Q lần lượt là trung điểm của JC, CD

Suy ra RQ là đường trung bình

Do đó RQ // JD, hay RI // JD

Xét tam giác BRI có J là trung điểm của BR và DJ // RI

Suy ra D là trung điểm của BI

Xét tam giác ABI có P, D lần lượt là trung điểm của AD, BI và PI cắt AD tại S

Suy ra S là trọng tâm tam giác ABI

Do đó SA = 2SD

Vậy ta chọn đáp án B.

Câu 38: Một người gửi ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm kể từ khi bắt đầu gửi tiền gần với kết quả nào sau đây:

A. 212 triệu;

B. 210 triệu;

C. 216 triệu;

D. 220 triệu.

Lời giải:

Đáp án đúng là: A

Sau 6 tháng đầu người đó nhận được số tiền là

A₁ = 100 . (1 + 2%)² = 104,04 (triệu đồng)

Số tiền người đó có ngay sau khi gửi thêm 100 triệu là:

104,04 + 100 = 204,04 (triệu đồng)

Số tiền người đó nhận được sau 1 năm là:

A₂ = 204,04 . (1 + 2%)² = 212,283 (triệu đồng) ≈ 212 triệu đồng

Vậy ta chọn đáp án A.

Câu 39: Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau, chia hết cho 5 và chữ số 2 luôn có mặt đúng một lần?

Lời giải:

Gọi số cần tìm là $\bar{a b c d e}$

+) TH1: e = 0

e có 1 cách chọn

Chữ số 2 có 4 cách chọn

Ba chỗ còn lại có 4 × 3 × 2 = 24 cách

Suy ra có 4 × 24 = 96 cách

+) TH2: e = 5; a = 2

a, e có 1 cách chọn

b có 4 cách chọn

c có 3 cách chọn

d có 2 cách chọn

Suy ra có 4 × 3 × 2 = 24 cách

+) TH3: e = 5; a ≠ 2

e có 1 cách chọn

a có 3 cách chon

Số 2 có 3 cách

Hai số còn lại có 3 × 2 = 6 cách

Suy ra có 3 × 3 × 6 = 54 cách

Vậy có tất cá 96 + 24 + 54 = 174 số thỏa mãn yêu cầu đề bài.

Câu 40: Chứng minh rằng n⁷ – n chia hết cho 7, với mọi n là số nguyên.

Lời giải:

Ta có n⁷ – n = n(n⁶ – 1)

= n(n³ – 1)(n³ + 1)

= n(n – 1)(n² + n + 1)(n + 1)(n² – n + 1)

= n(n² – 1)(n² + n + 1)(n² – n + 1)

Nếu n = 7k (k ∈ ℤ) thì n ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 1 (k ∈ ℤ) thì n² – 1 = 49k² + 14k ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 2 (k ∈ ℤ) thì n² + n + 1 = 49k² + 35k + 7 ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 3 (k ∈ ℤ) thì n² – n + 1 = 49k² + 35k + 7 ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 4 (k ∈ ℤ) thì n² + n + 1 = 49k² + 35k + 21 ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 5 (k ∈ ℤ) thì n² – n + 1 = 49k² + 70k + 21 ⋮ 7 khi đó n⁷ – n ⋮ 7

Nếu n = 7k + 6 (k ∈ ℤ) thì n² – 1 = 49k² + 84k + 35 ⋮ 7 khi đó n⁷ – n ⋮ 7

Vậy n⁷ – n chia hết cho 7, với mọi n là số nguyên.

Câu 41: Hỏi có bao nhiêu cách chọn ra hai số khác nhau trong các số tự nhiên từ 1 đến 20 sao cho tích của chúng chia hết cho 9?

Lời giải:

Để tích của chúng chia hết cho 9 thì đó là tích của hai số chia hết cho 3 hoặc là tích của một số chia hết cho 9 và một số không chia hết cho 3

Từ 1 đến 20 có các số chia hết cho 3 là: 3, 6, 9, 12, 15, 18 tổng cộng 6 số

Từ 1 đến 20 có các số chia hết cho 9 là: 9,18 tổng cộng có 2 số

Trường hợp 1: tích của hai số chia hết cho 3

Chọn 2 số từ 6 số ta có

6 × 5 : 2 = 15 cách

Trường hợp 2: tích của một số chia hết cho 9 và một số không chia hết cho 3

Có 2 số chia hết cho 9 và 14 số không chia hết cho 3 nên tổng số cách là

2 × 14 = 28 cách

Vậy có tổng số cách là: 15 + 28 = 43 cách.

Câu 42: Trên mặt phẳng tọa độ Oxy cho A(1; –1), B(2; 1) và C(4; 5). Ba điểm A, B, C có thẳng hàng không?

Lời giải:

Ta có: $\vec{A B} = (1; 2); \vec{A C} = (3; 6)$

Do $\frac{1}{3} = \frac{2}{6}$ nên $\vec{A B}, \vec{A C}$ cùng phương hay ba điểm A; B; C thẳng hàng.

Câu 43: Một tam giác có chu vi bằng 36 cm cạnh của nó tỉ lệ với 3; 4; 5. Tính độ dài ba cạnh.

Lời giải:

Gọi độ dài 3 cạnh của tam giác là a, b, c (a, b, c > 0)

Áp dụng tính chất dãy tỉ số bằng nhau ta có

$\frac{a}{3} = \frac{b}{4} = \frac{c}{5} = \frac{a + b + c}{3 + 4 + 5} = \frac{36}{12} = 3$

Suy ra $\frac{a}{3} = 3 \Leftrightarrow a = 9$ ;

$\frac{b}{4} = 3 \Leftrightarrow b = 12$ ;

$\frac{c}{5} = 3 \Leftrightarrow c = 15$

Vậy độ dài 3 cạnh của tam giác đó là 9 cm, 12 cm, 15 cm.

Từ khóa :

Giải bài tập

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

227

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236