Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12)

Ngọc Nguyễn Ngày: 13-06-2023 Tổng hợp kiến thức

436

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12)

Câu 1: Tìm ƯCLN của:

a) 10; 20 và 70;

b) 25; 55 và 75;

c) 80 và 144;

d) 63 và 2970.

Lời giải:

a) Ta có: 10 = 2. 5; 20 = 2². 5; 70 = 2. 5. 7.

Suy ra ƯCLN(10, 20, 70) = 2. 5 = 10.

b) Ta có: 25 = 5²; 55 = 5. 11; 75 = 5². 3.

Suy ra ƯCLN(25, 55, 75) = 5.

c) Ta có: 80 = 2⁴. 5; 144 = 2⁴. 3².

Suy ra ƯCLN(80, 144) = 2⁴ = 16.

d) Ta có: 63 = 3². 7; 2970 = 2. 3³. 5. 11.

Suy ra ƯCLN(63, 2970) = 3² = 9.

Câu 2: Tìm ƯCLN và tập hợp ước chung của các số sau:

a) 10; 20; 70;

b) 5661; 5291; 4292.

Lời giải:

a) Ta có: 10 = 2. 5; 20 = 2². 5; 70 = 2. 5. 7.

Vậy ƯC(10, 20, 70) = {1; 2; 5; 10}

Suy ra ƯCLN(10, 20, 70) = 10.

b) Ta có: 5661 = 3². 17. 37;

5291 = 11. 13. 37;

4292 = 2². 29. 37.

Vậy ƯC(5661, 5291, 4292) = {1; 37}.

Suy ra ƯCLN(5661, 5291, 4292) = {37}.

Câu 3: Tìm điều kiện của a và b để M xác định và rút gọn M:

$M = \frac{2 a + 2 a \sqrt{2} - 2 \sqrt{3 a b} + 2 \sqrt{3 a b} - 3 b - 2 a \sqrt{2}}{a \sqrt{2} + \sqrt{3 a b}}$ .

A. a > 0 và b ≥ 0; $M = \frac{\sqrt{2 a} - \sqrt{3 a}}{\sqrt{a}}$ ;

B. a < 0 và b ≥ 0; $M = \frac{\sqrt{2 a} - \sqrt{3 b}}{\sqrt{a}}$ ;

C. a > 0 và b < 0; $M = \frac{\sqrt{2 a} - \sqrt{3 b}}{\sqrt{a}}$ ;

D. a < 0 và b < 0; $M = \frac{\sqrt{2 a} - \sqrt{3 a}}{\sqrt{a}}$ .

Lời giải:

Đáp án đúng là: A

ĐKXĐ: a, b ≥ 0 và a ≠ 0 $\Leftrightarrow$ a > 0 và b ≥ 0

$M = \frac{2 a + 2 a \sqrt{2} - 2 \sqrt{3 a b} + 2 \sqrt{3 a b} - 3 b - 2 a \sqrt{2}}{a \sqrt{2} + \sqrt{3 a b}}$

$= \frac{2 a - 3 b}{a \sqrt{2} + \sqrt{3 a b}} = \frac{(\sqrt{2 a} + \sqrt{3 b}) (\sqrt{2 a} - \sqrt{3 b})}{\sqrt{a (\sqrt{2 a} + \sqrt{3 b})}}$

$= \frac{\sqrt{2 a} - \sqrt{3 b}}{\sqrt{a}}$ .

Câu 4: Tìm điều kiện để a, b để A = [a; a + 1] giao B = [b – 1; b + 2] khác rỗng.

Lời giải:

Để A ∩ B = Ø $\Leftrightarrow [\begin{array}{l} a + 1 < b - 1 \\ b + 2 < a \end{array} \Leftrightarrow [\begin{array}{l} a - b < - 2 \\ a - b > 2 \end{array}$ .

Suy ra A ∩ B ≠ Ø khi và chỉ khi xảy ra đồng thời a – b ≥ −2 và a – b ≤ 2.

Do đó −2 ≤ a – b ≤ 2.

Vậy đê A giao B khác rỗng thì −2 ≤ a – b ≤ 2.

Câu 5: Giá trị của m để đồ thị hàm số y = (m – 1)x + m cắt trục tung tại điểm có tung độ bằng 2 là

A. m = 1;

B. m = 2;

C. m = −1;

D. m = −2.

Lời giải:

Đáp án đúng là: B

Đồ thị hàm số cắt trục tung tại điểm của tung độ bằng 2 nên đồ thị của hàm số đi qua điểm A(0; 2) nên ta có:

2 = (m – 1). 0 + m ⇔ m = 2.

Vậy với m = 2 thì đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng 2.

Câu 6: Cho hàm số y = (m – 1)x + m.

a) Xác định giá trị của m để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.

b) Tìm tọa độ giao điểm của đường thẳng tìm được ở phần a và đường thẳng $y = \frac{1}{2} x + \frac{3}{2}$ bằng tính toán.

Lời giải:

a) Đồ thị hàm số cắt trục tung tại điểm của tung độ bằng 2 nên đồ thị của hàm số đi qua điểm A(0; 2) nên ta có:

2 = (m – 1). 0 + m ⇔ m = 2.

Vậy với m = 2 thì đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng 2.

b) Với m = 2 ta có đồ thị hàm số y = x + 2.

Xét phương trình hoành độ giao điểm, ta có:

$x + 2 = \frac{1}{2} x + \frac{3}{2} \Leftrightarrow x - \frac{1}{2} x = \frac{3}{2} - 2 \Leftrightarrow \frac{1}{2} x = \frac{- 1}{2}$

⇔ x = −1

⇒ y = −1 + 2 = 1.

Vậy tọa độ giao điểm cần tìm A(−1; 1).

Câu 7: Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A, N, H, M cùng nằm trên đường tròn nào?

A. (I; IM), I là trung điểm MN;

B. (I; IH), I là trung điểm MN;

C. (F; FA), F là giao điểm đường tròn với AH;

D. (E; EA), E là trung điểm AH.

Lời giải:

Đáp án đúng là: D

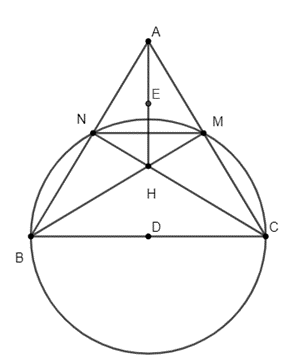
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 1)

Ta có: ∆BNC vuông tại N và ∆BMC vuông tại M. (do đường tròn đường kính BC đi qua M, N).

Xét ∆ANH và ∆AMH lần lượt vuông tại N, M.

Với E là trung điểm AH mà AH là cạnh huyền của cả hai tam giác ∆ANH và ∆AMH nên đường tròn tâm (E, EA) sẽ đi qua M, N, H.

Câu 8: Tìm tọa độ điểm D sao cho ABCD là hình bình hành biết A(4; 3), B(−1; 2), C(1; −1).

Lời giải:

Giả sử điểm D có tọa độ là D(a; b).

$\Rightarrow \overset{⇀}{D C} = (1 - a; - 1 - b)$ và $\vec{A B} = (- 5; - 1)$

Ta có ABCD là hình bình hành khi $\vec{D C} = \vec{A B}$

$\Leftrightarrow \{\begin{cases} 1 - a = - 5 \\ - 1 - b = - 1 \end{cases} \Leftrightarrow \{\begin{cases} a = 6 \\ b = 0 \end{cases}$ .

Vậy D(6; 0).

Câu 9: Trong mặt phẳng Oxy, cho A(−2; 0); B(5; −4); C(−5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là

A. D(−12; 5);

B. D(12; 5);

C. D(8; 5);

D. (8; −5).

Lời giải:

Đáp án đúng là: A

Gọi tọa độ của D(x; y).

Khi đó $\vec{A D} (x + 2; y)$ ; $\vec{B C} (- 10; 5)$ .

Ta có tứ giác ABCD là hình bình hành khi $\vec{B C} = \vec{A D}$

$\Leftrightarrow \{\begin{cases} x + 2 = - 10 \\ y = 5 \end{cases} \Leftrightarrow \{\begin{cases} x = - 12 \\ y = 5 \end{cases}$ .

Vậy tọa độ của D là: D(−12; 5).

Câu 10: Chứng minh rằng với mọi số thực a, b ta luôn có: a² + b² ≥ 2ab.

Lời giải:

Với mọi số thực a, b ta có: (a – b) ≥ 0

⇔ a² – 2ab + b² ≥ 0

⇔ a² + b² ≥ 2ab (đpcm).

Vậy với mọi số thực a, b ta luôn có a² + b² ≥ 2ab.

Câu 11: a) Chứng minh rằng a² + ab + b² ≥ 0 với mọi số thực a, b.

b) Chứng minh với 2 số thực a, b tùy ý, ta có a⁴ + b⁴ ≥ a³b + ab³.

Lời giải:

a) Ta có: a² + ab + b² $= a^{2} + \frac{2 a b}{4} + {(\frac{b}{2})}^{2} + \frac{3 b^{2}}{4}$

$= {(a + \frac{b}{2})}^{2} + \frac{3 b^{2}}{4} \geq 0$ $\forall a, b \in ℝ$ .

Vậy suy ra a² + ab + b² ≥ 0 $\forall a, b \in ℝ$ .

b) Ta có: a⁴ + b⁴ ≥ a³b + ab³

$\Leftrightarrow$ a³(a – b) – b³(a – b) ≥ 0

$\Leftrightarrow$ (a³ – b³)(a – b) ≥ 0

$\Leftrightarrow$ (a – b)²(a² + ab + b²) ≥ 0 $\forall a, b \in ℝ$ .

Do đó: a⁴ + b⁴ ≥ a³b + ab³ $\forall a, b \in ℝ$ .

Câu 12: Rút gọn biểu thức: $A = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{3} + \sqrt{4}}$ .

Lời giải:

Ta có $A = \frac{1}{\sqrt{1} + \sqrt{2}} + \frac{1}{\sqrt{3} + \sqrt{4}}$

$= \frac{(1 - \sqrt{2})}{(1 + \sqrt{2}) (1 - \sqrt{2})} + \frac{(\sqrt{3} - \sqrt{4})}{(\sqrt{3} + \sqrt{4}) (\sqrt{3} - \sqrt{4})}$

$= \frac{1 - \sqrt{2}}{1 - 2^{2}} + \frac{\sqrt{3} - 2}{3 - 4}$

$= \sqrt{2} - 1 + 2 - \sqrt{3} = 1 + \sqrt{2} - \sqrt{3}$ .

Câu 13: Đổi một số đơn vị sau:

a) … km/h = 5 m/s;

b) 12 m/s = … km/h;

c) 48 km/h = … m/s;

d) 150 cm/s = … m/s = .... km/h;

Lời giải:

Đổi 1 km = 1000 m; 1 h = 3 600 s.

Suy ra $1 m = \frac{1}{1 000} k m$ ; $1 s = \frac{1}{3 600} h$ .

Do đó 1 (m/s) = $\frac{1}{1000} : \frac{1}{3600}$ (km/h) = 3,6 (km/h).

Khi đó ta có:

a) 18 km/h = 5 m/s.

b) 12 m/s = 43,2 km/h.

c) 48 km/h = $\frac{40}{3}$ m/s

d) 150 cm/s = 1,5 m/s = 5,4 km/h.

Câu 14: Cho hàm số $y = \frac{\ln x - 6}{\ln x - 2 m}$ với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng (1; e). Số phần tử của S là

A. 3;

B. 4;

C. 1;

D. 2.

Lời giải:

Đáp án đúng là: D

Xét $y = \frac{\ln x - 6}{\ln x - 2 m}$ có điều kiện $\{\begin{cases} \ln x \neq 2 m \\ x > 0 \end{cases}$ .

Vì x ∈ (1; e) nên ln x ∈ (0; 1).

Ta có: $y' = \frac{6 - 2 m}{{(\ln x - 2 m)}^{2}} . \frac{1}{x}$ .

Hàm số đồng biến trên khoảng (1; e) nên ta có:

$\{\begin{cases} 6 - 2 m > 0 \\ 2 m \notin (0; 1) \end{cases} \Leftrightarrow \{\begin{cases} m < 3 \\ m \notin (0; \frac{1}{2}) \end{cases}$ .

Mà m là số nguyên dương nên m ∈ {1; 2}.

Vậy số phần tử của S là 2.

Câu 15: Cho hàm số $y = \frac{\ln x - 4}{\ln x - 2 m}$ với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng (1; e). Tìm số phần tử của S.

A. 3;

B. 2;

C. 1;

D. 4.

Lời giải:

Đáp án đúng là C.

Ta có $y = f (x) = \frac{\ln x - 4}{\ln x - 2 m}$ .

Đặt t = ln x, điều kiện t ∈ (0; 1).

Khi đó $g (t) = \frac{t - 4}{t - 2 m}; g' (t) = \frac{- 2 m + 4}{{(t - 2 m)}^{2}}$ .

Để hàm số f(x) đồng biến trên (1; e) thì hàm số g(t) đồng biến trên (0; 1)

$\Rightarrow$ g’(t) > 0, t ∈ (0; 1) $\Leftrightarrow \frac{- 2 m + 4}{{(t - 2 m)}^{2}} > 0$ , t ∈ (0;1)

$\Leftrightarrow \{\begin{cases} - 2 m + 4 > 0 \\ 2 m \notin (0; 1) \end{cases} \Leftrightarrow [\begin{array}{l} \frac{1}{2} \leq m < 2 \\ m \leq 0 \end{array}$ .

Mà S là tập hợp các số nguyên dương nên suy ra S = {1}.

Vậy số phần tử của tập S là 1.

Câu 16: Số điểm biểu diễn của nghiệm của phương trình $\sin (2 x + \frac{π}{3}) = \frac{1}{2}$ trên đường tròn lượng giác là

A. 4;

B. 6;

C. 1;

D. 2.

Lời giải:

Đáp án đúng là A

Ta có: $\sin (2 x + \frac{π}{3}) = \frac{1}{2}$

$\Leftrightarrow [\begin{array}{l} 2 x + \frac{π}{3} = \frac{π}{6} + k 2 π \\ 2 x + \frac{π}{3} = \frac{5 π}{6} + k 2 π \end{array}$ (k ∈ ℤ)

$\Leftrightarrow [\begin{array}{l} x = - \frac{π}{12} + k π \\ x = \frac{π}{4} + k \end{array}$ (k ∈ ℤ).

Ta thấy mỗi họ nghiệm sẽ biểu diễn được 2 điểm khác nhau và khác điểm của họ nghiệm của nên số điểm biểu diễn các nghiệm là 4.

Câu 17: Trên đường tròn lượng giác số điểm biểu diễn tập nghiệm của phương trình $2 \sin 3 x - \sqrt{3} \cos x = \sin x$ là

A. 2;

B. 6;

C. 8;

D. 4.

Lời giải:

Ta có: $2 \sin 3 x - \sqrt{3} \cos x = \sin x$

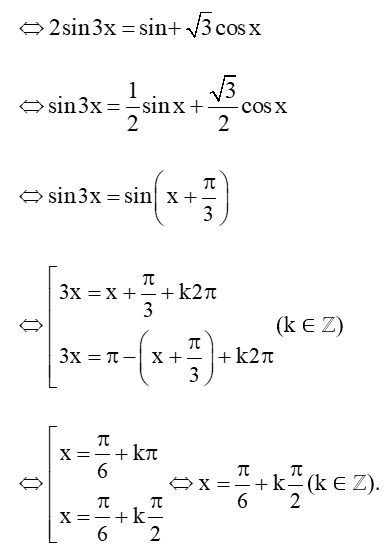
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 2)

Vì $x = \frac{π}{6} + k \frac{π}{2} = \frac{π}{6} + k \frac{2 π}{4}$ (k ∈ ℤ) nên ta có 4 điểm biểu diễn tập nghiệm của phương trình trên đường tròn lượng giác.

Câu 18: Tính chu vi tam giác ABC biết AB = 6 và 2sinA = 3sinB = 4sinC.

A. 26;

B. 13;

C. $5 \sqrt{26}$ ;

D. $10 \sqrt{6}$ .

Lời giải:

Đáp án đúng là A.

Ta có: $\frac{A B}{\sin C} = \frac{B C}{\sin A} = \frac{C A}{\sin B}$

$\Rightarrow \{\begin{cases} B C = \frac{\sin A}{\sin C} . A B \\ C A = \frac{\sin B}{\sin C} . A B \end{cases}$

$\Rightarrow \{\begin{cases} B C = 2.6 = 12 \\ C A = \frac{4}{3} .6 = 8 \end{cases}$ .

Vậy chu vi tam giác ABC là: AB + BC +CA = 6 + 12 + 8 = 26.

Câu 19: Phân tích đa thức thành nhân tử:

a) x(x – 1) – y(1 – x);

b) x³ + x²+ y³ + xy.

Lời giải:

a) x(x – 1) – y(1 – x) = x(x – 1) + y(x – 1)

= (x + y)(x – 1).

b) x³ + x²+ y³ + xy = (x³ + y³) + (x² + xy)

= (x + y)(x² – xy + y²) + x(x + y)

= (x + y)(x² – xy + y² + x).

Câu 20: Tính giá trị của biểu thức: x(x – 1) – y(1 – x) tại x = 2001 và y = 1999.

Lời giải:

Ta có: x(x – 1) – y(1 – x) = x(x – 1) + y(x – 1)

= (x + y)(x – 1).

Khi đó tại x = 2001 và y = 1999, giá trị của biểu thức bằng:

(2001 + 1999)(2001 – 1) = 4000. 2000 = 8 000 000.

Câu 21: Cho hàm số y = (2m – 1)x – m + 2. Tìm m để đồ thị hàm số đi qua A(1; 2):

A. y = x + 2;

B. y = x – 1;

C. y = −x + 1;

D. y = x + 1.

Lời giải:

Đáp án đúng là D

Vì đồ thị hàm số đi qua điểm A(1; 2) nên ta có:

2 = (2m – 1). 1 – m + 2 ⇔ m = 1.

Vậy hàm số thỏa mãn yêu cầu bài toán là: y = x + 1.

Câu 22: Cho hàm số y = (2 + m)x – 4.

a) Tìm m để đồ thị hàm số đi qua A(−1; 2);

b) Vẽ đồ thị hàm số với m vừa tìm được và tìm giao điểm của đường thẳng đó với đường thẳng y = 2x – 4.

Lời giải:

a) Vì đồ thị hàm số đi qua điểm A(−1; 2) nên ta có:

2 = (2 + m).(−1) – 4

⇔ − m = 8

⇔ m = −8.

Vậy hàm số thỏa mãn yêu cầu bài toán là: y = −6x – 4.

b) Đồ thị hàm số y = −6x – 4:

Nếu y = 2 thì x = −1 suy ra A (−1; 2).

Nếu x = 0 thì y = −4 suy ra B (0; −4).

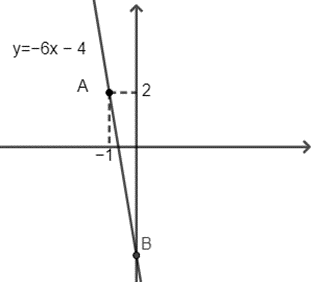
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 4)

Xét phương trình hoành độ giao điểm của hai đồ thị ta có:

−6x – 4 = 2x – 4

⇔ −8x = 0

⇔ x = 0.

Thay x = 0 vào y = 2x – 4 ta được: y = −4.

Vậy tọa độ giao điểm của hai đồ thị hàm số là (0; −4).

Câu 23: Cho tam giác ABC có $\hat{A} = 80 °$ ; $\hat{B} = 50 °$ . Chứng minh tam giác ABC cân.

Lời giải:

Trong tam giác ABC ta có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ .

Suy ra $\hat{C} = 180 ° - \hat{A} - \hat{B} = 180 ° - 80 ° - 50 ° = 50 °$ .

Khi đó ta thấy $\hat{B} = \hat{C} = 50 °$ .

Suy ra tam giác ABC cân tại A.

Câu 24: Cho hình thang cân ABCD (AB//CD). Gọi E là trung điểm cạnh AB. Gọi I, K, M lần lượt là trung điểm của BC, CD, DA.

a) Tứ giác EIKM là hình gì?

b) Tìm điều kiện của hình thang ABCD để EIKM là hình vuông.

Lời giải:

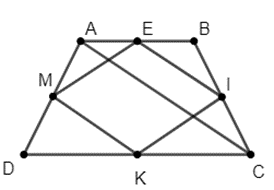
a) Xét tam giác ABC có E; I lần lượt là trung điểm của AB và BC.

Suy ra ta có EI là đường trung bình của tam giác ABC.

Do đó EI // AC, $E I = \frac{1}{2} A C$ (1)

Chứng minh tương tự ta có: MK // AC, $M K = \frac{1}{2} A C$ (2)

ME // BD, $M E = \frac{1}{2} B D$ (3)

Mặt khác AC = BD (do tứ giác ABCD là hình thang cân) (4)

Từ (3) và (4) suy ra $M E = \frac{1}{2} A C = M K$ (5)

Từ (1); (2); (5) suy ra tứ giác EIKM là hình thoi.

b) Để tứ giác EIMK là hình vuông thì EM ⊥ EI.

Mà theo câu a) ta có: EI // AC; EM // BD.

Khi đó suy ra để tứ giác EIMK là hình vuông thì AC ⊥ BD.

Câu 25: Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.

a) Tứ giác MNPQ là hình gì? Vì sao?

b) Chứng minh ABCD là hình thang cân thì MP là phân giác của góc QMN.

Lời giải:

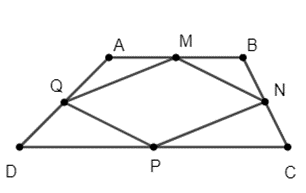
a) Xét tam giác ABC có M, N lần lượt là trung điểm của AB và BC.

Suy ra MN là đường trung bình của tam giác ABC.

Do đó MN // AC, $M N = \frac{1}{2} A C$ (1)

Chứng minh tương tự, ta có: QP//AC, $Q P = \frac{1}{2} A C$ (2)

QM // BD, $Q M = \frac{1}{2} B D$ (3)

Từ (1) và (2) suy ra tứ giác MNPQ là hình bình hành.

b) Khi ABCD là tam giác cân với AB // CD ta có AC = BD.

Từ (3) suy ra: $Q M = \frac{1}{2} B D = \frac{1}{2} A C = M N$ (4)

Theo câu a) MNPQ là hình bình hành mà mặt khác tứ giác MNPQ có QM = MN mà QM và MN là hai cạnh kề nên suy ra MNPQ là hình thoi.

Do đó MP là tia phân giác của $\hat{Q M N}$ theo tính chất của hình thoi.

Câu 26: Cho tam giác ABC nhọn (AB < AC), đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC. Tính AH, MH biết AM = 8 cm; BM = 2 cm.

Lời giải:

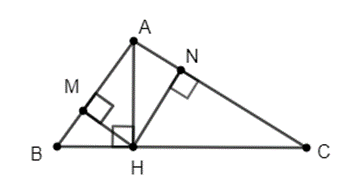
Xét ∆AHB vuông tại H có đường cao MH nên ta có: MH² = MB.MA.

Do đó $M H = \sqrt{8 . 2} = \sqrt{16} = 4$ (cm).

Áp dụng định lý Py−ta−go vào ∆AMH vuông tại M, ta có:

$A H = \sqrt{A M^{2} + M H^{2}} = \sqrt{8^{2} + 4^{2}} = 4 \sqrt{5}$ (cm).

Vậy $A H = 4 \sqrt{5}$ cm; MH = 4 cm.

Câu 27: Giá trị nhỏ nhất của hàm số y = sin²x + 2cos²x.

Lời giải:

Ta có: y = sin²x + 2cos²x

= sin²x + cos²x + cos²x

= 1 + cos²x (vì sin²x + cos²x = 1)

Ta có 1 ≤ 1 + cos²x ≤ 2 (do 1 ≤ cosx ≤ 2).

Suy ra Miny = 1 hay 1 + cos²x = 1

⇔ cos²x = 0 ⇔ cosx = 0

$\Leftrightarrow x = \frac{π}{2} + k π$ (k ∈ ℤ).

Câu 28: Cho hàm số y = kx + 3 – 2x + k.

a) Xác định k để hàm số là hàm bậc nhất đồng biến.

b) Xác định k để đồ thị là đường thẳng đi qua M(1; 2).

Lời giải:

Đặt (d): y = kx + 3 – 2x + k = (k – 2)x + k + 3.

a) Để (d) là hàm bậc nhất đồng biến thì k – 2 > 0 hay k > 2.

Vậy với k > 2 thì hàm số là hàm bậc nhất đồng biến.

b) Vì đồ thị hàm số (d) đi qua M(1; 2) vào ta có:

(k – 2). 1 + k + 3 = 2

⇔ 2k = 1

$\Leftrightarrow k = \frac{1}{2}$ .

Vậy $k = \frac{1}{2}$ thỏa mãn yêu cầu bài toán.

Câu 29: Một mảnh đất hình chữ nhật có chu vi 40 m, chiều dài hơn chiều rộng 400 cm. Tính diện tích của mảnh đất đó.

Lời giải:

Đổi: 400 cm = 4 m.

Nửa chu vi mảnh đất đó là: 40 : 2 = 20 (m)

Chiều dài của mảnh đất là: (20 + 4) : 2 = 12(m)

Chiều rộng của mảnh đất là: 20 – 12 = 8 (m)

Diện tích mảnh đất đó là: 12 . 8 = 96 (m²).

Vậy diện tích của mảnh đất đó là 96 m².

Câu 30: Một mảnh đất hình chữ nhật có chu vi bằng 40 m. Nếu tăng chiều rộng thêm 2 m giảm chiều dài đi 2 m thì diện tích tăng thêm 4 m². Tính chiều dài, chiều rộng ban đầu của hình chữ nhật.

Lời giải:

Gọi chiều rộng hình chữ nhật là x (x > 0), chiều dài hình chữ nhật là y (y > 0).

Ta có chu vi hình chữ nhật bằng 40 nên (x + y) . 2= 40

x + y = 20 ⇔ y = 20 – x

Vì tăng chiều rộng thêm 2 m giảm chiều dài đi 2 m thì diện tích tăng thêm 4 m² nên: (x + 2)(y − 2)= xy + 4

⇔ xy − 2x + 2y − 4= xy + 4

⇔ x – y + 4 = 0

⇔ x − (20 − x) + 4 = 0

⇔ 2x = 16

⇔ x = 8

Suy ra y = 12.

Vậy chiều rộng của hình chữ nhật là 8 m, chiều dài của hình chữ nhật là 12 m.

Câu 31: Cho parabol (P): y = −2x² và đường thẳng (d): y= (m + 1)x – m – 3 (m là tham số). Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt (P) tại điểm có hoành độ bằng −1.

Lời giải:

Xét phương trình hoành độ giao điểm của (P) và (d) ta có:

−2x² = (m + 1)x – m – 3

⇔ −2x² – (m + 1)x + m + 3 = 0. (*)

Để đường thẳng (d) cắt (P) tại điểm có hoành độ bằng −1 thì phương trình (*) có nghiệm là x = −1.

Khi đó ta có: −2 + (m + 1) + m + 3 = 0

⇔ 2m = 2 ⇔ m = 1.

Vậy với m = 1 thì thỏa mãn yêu cầu bài toán.

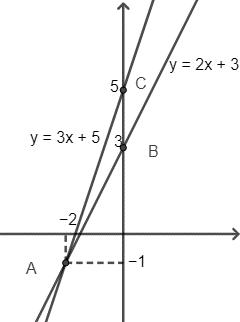
Câu 32: Vẽ đường thẳng (d₁): y = 2x + 3 và (d₂) : y = (m + 1)x + 5 khi m = 2.

Lời giải:

Với m = 2 ta có (d₂): y = 3x + 5.

Xét phương trình hoành độ giao điểm:

2x + 3 = 3x + 5

⇔ x = −2 ⇒ y = −1.

Vậy giao điểm của (d₁) và (d₂) là: A(−2; −1).

Với x = 0 ta có điểm B(0; 3) ∈ (d₁); C(0; 5) ∈ (d₂).

Vậy ta có đồ thị hàm số:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 8)

Câu 33: Cho phương trình (m + 1)x² + 2mx + m – 1 = 0 (*).

Tìm m để phương trình có hai nghiệm x₁, x₂ sao cho x₁² + x₂² = 5.

Lời giải:

Để phương trình có hai nghiệm phân biệt ta có:

$\{\begin{cases} Δ' > 0 \\ a \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} - (m + 1) (m - 1) > 0 \\ m \neq - 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} m^{2} - m^{2} + 1 > 0 \\ m \neq - 1 \end{cases} \Leftrightarrow m \neq - 1$ .

Áp dụng định lý Vi−ét ta có: $\{\begin{cases} x_{1} + x_{2} = \frac{- 2 m}{m + 1} \\ x_{1} . x_{2} = \frac{m - 1}{m + 1} \end{cases}$

Khi đó, ta có: x₁² + x₂² = 5 ⇔ (x₁ + x₂)² – 2x₁x₂ = 5

$\Leftrightarrow {(\frac{- 2 m}{m + 1})}^{2} - 2 \frac{m - 1}{m + 1} = 5$

⇔ 4m² – 2(m – 1)(m + 1) = 5(m + 1)²

⇔ 4m² – 2m² + 2 = 5m² + 10m + 5

⇔ 3m² + 10m + 3 = 0

$\Leftrightarrow [\begin{array}{l} m = - 3 \\ m = \frac{- 1}{3} \end{array}$ (thỏa mãn điều kiện).

Vậy có hai giá trị của m thỏa mãn điều kiện m = −3; $m = \frac{- 1}{3}$ .

Câu 34: Cho hình vuông ABCD cạnh a. Tính độ dài vectơ $\vec{A B} + \vec{A C}$ .

Lời giải:

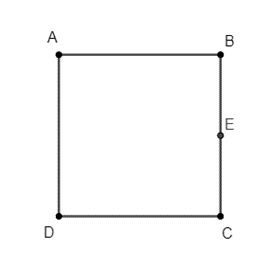
Gọi E là trung điểm của BC ta có:

$\vec{A B} + \vec{A C} = (\vec{A E} + \vec{E B}) + (\vec{A E} + \vec{E C})$

$= 2. \vec{A E} + \vec{E B} + \vec{E C} = 2 \vec{A E} + \vec{0} = 2 \vec{A E}$

Mặt khác ta có: $|\vec{A E}| = A E = \frac{\sqrt{5} a}{2}$

Do đó $2 |\vec{A E}| = a \sqrt{5}$ .

Vậy $|\vec{A B} + \vec{A C}| = a \sqrt{5}$ .

Câu 35: Viết phương trình đường thăng (d) đi qua điểm A(1; 1) và cách điểm B(−2; 2) một khoảnh bằng $\sqrt{5}$ .

Lời giải:

Giả sử đường thẳng (d) cần tìm có vectơ pháp tuyến $\vec{n} = (a; b)$ với a² + b² ≠ 0.

Khi đó (d) có phương trình: Ax + bx – a – b = 0

Do d(B; (d)) = $\sqrt{5}$ , ta có phương trình:

$\frac{|- 2 a + 2 b - a - b|}{\sqrt{a^{2} + b^{2}}} = \sqrt{5} \Leftrightarrow |b - 3 a| = \sqrt{5 a^{2} + 5 b^{2}}$

⇔ b² – 6ab + 9a² = 5a² + 5b²

⇔ 2a² – 3ab – 2b² = 0

$\Leftrightarrow \{\begin{cases} a = - 2 b \\ a = \frac{- 1}{2} b \end{cases}$ .

Với a = 2b. do a² + b² ≠ 0 nên chọn a = 2, b = 1 thu được đường thẳng

(d₁): 2x + y – 3 = 0

Với $a = \frac{- 1}{2} b$ , do a² + b² ≠ 0 nên chọn a = 1, b = −2 thu được đường thẳng

(d₂): x – 2y + 1 = 0.

Câu 36: Xác định a, b, c biết parabol y = ax² + bx + c đi qua điểm A(8; 0) và có đỉnh là I(6; −12).

Lời giải:

• Parabol y = ax² + bx + c đi qua điểm A (8; 0) nên

0 = a.8² + b.8 + c ⟺ 64a + 8b + c = 0 (1).

• Parabol y = ax² + bx + c có đỉnh là I (6; –12) suy ra:

$\frac{- b}{2 a} = 6$ ⇒ b = –12a (2).

$\frac{- Δ}{4 a} = - 12$ ⇒ Δ = 48a ⇒ b² – 4ac = 48a (3) .

Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⟺ c = 32a.

Thay b = –12a và c = 32a vào (3) ta được:

(–12a)² – 4a.32a = 48a

⟺ 144a² – 128a² = 48a

⟺ 16a² = 48a

⟺ a = 3 (vì a ≠ 0).

Từ a = 3 ⇒ b = –36 và c = 96.

Vậy a = 3; b = –36 và c = 96 thỏa mãn yêu cầu bài toán.

Câu 37: Cho hình vuông ABCD có cạnh bằng a. Khi đó giá trị $|\vec{A C} + \vec{B D}|$ bằng bao nhiêu?

A. $2 a \sqrt{2}$ ;

B. 2a;

C. a;

D. 0.

Lời giải:

Đáp án đúng là: B

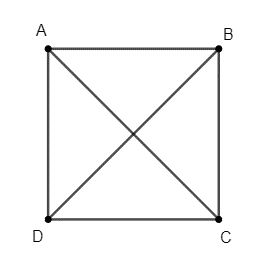
Ta có: ${|\vec{A C} + \vec{B D}|}^{2} = A C^{2} + 2. \vec{A C} . \vec{B D} + B D^{2}$ (do AC ⊥ BD)

= AC² + BD² = 2a² +2a² = 4a²

Suy ra: $|\vec{A C} + \vec{B D}| = 2 a$ .

Câu 38: Cho hình bình hành ABCD. Gọi d là đường thẳng qua A và không cắt đoạn thẳng BD. Gọi BB’, CC’, DD’ lần lượt là khoảng cách từ B, C, D đến đường thẳng d (B’, C’, D’ ∈ (d)). Chứng minh rằng BB’ + DD’ = CC’.

Lời giải:

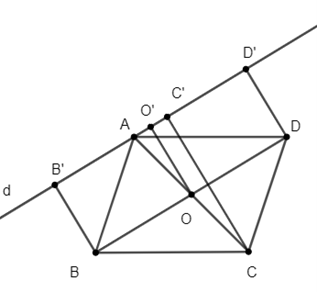
Gọi O là giao điểm của AC và BD. ABCD là hình bình hành nên O là trung điểm của AC và BD. Vẽ OO’⊥ d, O’ ∈ d.

Các đường thẳng BB’, CC’, DD’, OO’ song song với nhau (vì cùng vuông góc với đường thẳng d).

Vì B’D’DB là hình thang (vì BB’ // DD) có OB = OD, OO’ // BB’ nên OO’ là đường trung bình của hình thang B’D’DB.

Do đó $O O' = \frac{1}{2} (B B' + D D')$ .

Mặt khác ∆ACC’ có OO’ // CC’ và OA = OC.

Nên OO’ là đường trung bình của tam giác ACC’, suy ra: $O O' = \frac{1}{2} C C'$ .

Từ (1) và (2) suy ra BB’ + DD’ = CC’.

Câu 39: Cho khối chóp S.ABCD có đáy ABCD là hình thang cân với đáy AD và BC. Biết AD = 2a, AB = BC = CD = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AD thỏa mãn HD = 3HA , SD tạo với đáy một góc 45°.Tính thể tích V của khối chóp S.ABCD.

Lời giải: :

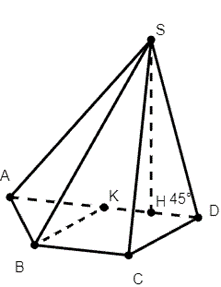
Gọi M là trung điểm của AD.

Ta có BC = AM = a và BC // AM nên tứ giác ABCM là hình bình hành.

Suy ra CM = AB = a suy ra ∆CDM đều.

Gọi K là hình chiếu của C lên AD.

Ta có: $C K = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2}$ .

Diện tích hình thang ABCD là : $S = \frac{(a + 2 a) . \frac{a \sqrt{3}}{2}}{2} = \frac{3 a^{2} \sqrt{3}}{4}$ .

Lại có: $H D = \frac{3}{2} .2 a = \frac{3 a}{2}$ .

Vậy thể tích của khối chóp S.ABCD là :

$V = \frac{1}{3} S H . S_{A B C D} = \frac{1}{3} . \frac{3 a}{2} . \frac{3 a^{2} \sqrt{3}}{4} = \frac{3 a^{3} \sqrt{3}}{8}$ (đvtt).

Vậy thể tích của khối chóp S.ABCD là $\frac{3 a^{3} \sqrt{3}}{8}$ đvtt.

Câu 40: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số a + b > 2 thì có ít nhất một số lớn hơn 1;

B. Trong một tam giác cân hai đường cao bằng nhau;

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau;

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3;

Lời giải:
Đáp án đúng là B

Khi đảo mệnh đề B ta có: Nếu một tam giác có hai đường cao ứng với hai cạnh bên bằng nhau bằng nhau thì tam giác đó là là một tam giác cân. Là một mệnh đề đúng.

Câu 41: x thuộc Ư(42) và x > 5.

Lời giải:
Ta có: 42 = 2 . 3 . 7.

Suy ra Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}.

Mà x > 5 suy ra x ∈ {6; 7; 14; 21; 42}.

Câu 42: Tìm ước của 15; 42 và ƯC(15, 42).

Lời giải:

Ta có: 15 = 3.5.

Suy ra: Ư(15) ={1; 3; 5; 15}.

42 = 2 . 3 . 7.

Suy ra Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}.

Vậy ƯC(15, 42} = {1; 3}.

Câu 43: Cho tam giác ABC M(1; 1), N(2; 3), P(0; 4) lần lượt là trung điểm các cạnh BC, CA, AB. Toạ độ các đỉnh tam giác là

A. A(1; −2), B(1; −6), C(3; 8);

B. A(1; −2), B(−1; −6), C(3; 8);

C. A(1; −2), B(−1; −6), C(−3; 8);

D. A(1; −2), B(−1; 6), C(3; 8).

Lời giải:

Đáp án đúng là: B.

Ta có PAN là hình bình hành nên:

$\vec{P A} = \vec{M N} \Rightarrow \{\begin{cases} x_{A} = 1 \\ y_{A} + 4 = 2 \end{cases} \Leftrightarrow \{\begin{cases} x_{A} = 1 \\ y_{A} = - 2 \end{cases}$

Tương tự ta có: $\{\begin{cases} x_{B} = - 1 \\ y_{B} = - 6 \end{cases}; \{\begin{cases} x_{C} = 3 \\ y_{C} = 8 \end{cases}$

Vậy tọa độ các đỉnh của tam giác là: A(1; −2), B(−1; −6), C(3; 8).

Câu 44: Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.

Chứng minh: AC + BD = CD và AC.BD không đổi.

Lời giải:

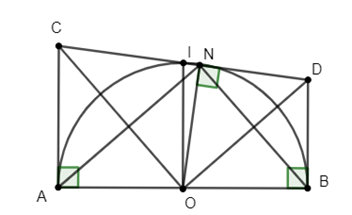
Ta có DN và DB là hai tiếp tuyến cắt nhau tại D suy ra DN = DB.

CA và CN là hai tiếp tuyến cắt nhau tại C suy ra CA = CN.

Khi đó: DB + CA = DN + CN = DC (đpcm).

Mặt khác OC và OD lần lượt là hai phân giác của hai góc $\hat{A O N}$ và $\hat{B O N}$ kề bù nên $\hat{C O D} = 90 °$ .

Trong tam giác vuông $Δ$ COD có ON là đường cao nên:

DN.CN = ON² = R².

Hay AC.BD = R² (không đổi) (đpcm).

Câu 45: Một bình chứa 16 viên bi trong đó có 7 viên bi trắng, 6 viên bi đen, 3 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Xác suất lấy được cả 3 viên bi đỏ là

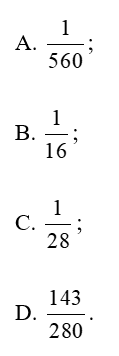
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 14)

Lời giải:

Đáp án đúng là: A

Số phần tử của không gian mẫu là: $n (Ω) = C_{16}^{3}$ .

Gọi A là biến cố: “Lấy được cả ba viên bi đỏ”.

$\Rightarrow n (A) = C_{3}^{3} \Rightarrow P_{A} = \frac{n (A)}{n (Ω)} = \frac{C_{3}^{3}}{C_{16}^{3}} = \frac{1}{560}$ .

Vậy xác suất lấy được cả 3 viên bi đỏ bằng $\frac{1}{560}$ .

Câu 46: Một bình chứa 16 viên bi trong đó có 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ. Lấy ngẫu nhiên trong bình đó 3 viên bi. Tính xác suất sao cho cả 3 viên bi được lấy ra không có viên nào màu đỏ.

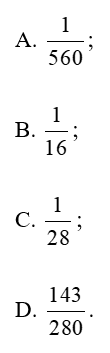
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 12) (ảnh 15)

Lời giải:

Đáp án đúng là: D.

Số phần tử của không gian mẫu là: $n (Ω) = C_{16}^{3}$ .

Gọi B là biến cố: “Lấy được 3 viên bi không phải bi đỏ”

Chọn 3 viên bi từ 13 viên bi không có viên bi đỏ: $n (B) = C_{13}^{3} = 286$ .

Suy ra xác xuất lấy được 3 viên bi không có bi đỏ là:

$P (B) = \frac{n (B)}{n (Ω)} = \frac{286}{560} = \frac{143}{280}$ .

Câu 47: Một tam giác có chiều cao bằng $\frac{3}{4}$ cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 dm². Tính diện tích của tam giác ban đầu.

A. 700 dm²;

B. 678 dm²;

C. 627 dm²;

D. 726 dm².

Lời giải:

Đáp án đúng là: D

Gọi chiều cao của tam giác là h (dm), cạnh đáy tam giác là a (dm) (a > 3, h > 0).

Diện tích tam giác ban đầu là $\frac{1}{2} a h$ (dm²).

Vì độ dài chiều cao bằng $\frac{3}{4}$ độ dài cạnh đáy nên ta có phương trình $h = \frac{3}{4} a$ .

Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 3 dm thì diện tích của nó tăng thêm 12 dm²nên ta có phương trình:

$\frac{1}{2} (h + 3) (a - 3) - \frac{1}{2} a h = 12$ .

Ta có hệ phương trình : $\{\begin{cases} h = \frac{3}{4} a \\ \frac{1}{2} (h + 3) (a - 3) - \frac{1}{2} a h = 12 \end{cases} \Rightarrow \{\begin{cases} a = 44 \\ h = 33 \end{cases}$ .

Vậy chiều cao của tam giác bằng 44 dm, cạnh đáy tam giác bằng 33 dm.

Suy ra diện tích tam giác ban đầu là $\frac{1}{2} . 44 . 33 = 726$ (dm²).

Câu 48: Chọn A(3; 4), B(2; 5). Tìm m để điểm C(−7; m) thuộc đường thẳng AB.

Lời giải:

Ta có: $\vec{A B} = (- 1; 1)$ ; $\vec{A C} = (- 10; m - 4)$ .

Để C thuộc đường thẳng AB thì: $\frac{- 1}{10} = \frac{1}{m - 4} \Leftrightarrow m = 14$ .

Vậy C(−7; 14).

Câu 49: Cho biểu thức A = (x – 3)³ – (x + 1)³ + 12x(x – 1).

a) Rút gọn biểu thức.

b) Tính giá trị của biểu thức của A tại x = 1.

Lời giải:

a) A = (x – 3)² – (x + 1)³ + 12x(x – 1)

= x³ – 9x² + 27x – 27 – x³ – 3x² – 3x – 1 + 12x² – 12x

= 12x – 28.

b) Thay x = 1 vào biểu thức A, ta được:

A = 12. 1 – 28 = −16.

Câu 50: Tìm x, biết:

5x(4x² – 2x + 1) – 2x(10x² – 5x + 2) = −36.

Lời giải:

5x(4x² – 2x + 1) – 2x(10x² – 5x + 2) = −36.

⇔ 20x³ – 10x + 5x – 20x³ + 10x – 4x + 36 = 0

⇔ x = −36.

Vậy x = −36.

Câu 51: Cho ba điểm A(1; 1), B(3; 2), C(m + 4; 2m + 1). Tìm m để 3 điểm A, B, C thẳng hàng.

Lời giải:

Ta có: $\vec{A B} = (1; 1)$ ; $\vec{A C} = (m + 3; 2 m)$

Để ba điểm A, B, C thẳng hàng thì $\vec{A B} = k \vec{A C}$

$\Leftrightarrow$ (2; 1) = k (m + 3; 2m)

$\Leftrightarrow$ $\frac{m + 3}{2} = \frac{2 m}{1}$

$\Leftrightarrow$ m + 3 = 4m

$\Leftrightarrow$ m = 1

Vậy với m =1 thì ba điểm A, B, C thẳng hàng.

Câu 52: Chứng minh rằng nếu (a² + b² + c²)(x² + y² + z²) = (ax + by + cz)² với x, y, z khác 0 thì $\frac{a}{x} = \frac{b}{y} = \frac{c}{z}$ .

Lời giải:

Ta có: (a² + b² + c²)(x² + y² + z²) = (ax + by + cz)²

⇔ a²x² + a²y² + a²z² + b²y² + b²z² + c²x² + c²y² + c²z² = a²x² + b²y² + c²z² + 2axby + 2axcz + 2bycz

⇔ a²y² + a²z² + b²x² + b²z² + c²x²+ c²y² – 2axby – 2axcz – 2bycz = 0

⇔ (a²y² – 2axby + b²x²) + (a²z² – 2axcz + c²x²) + (b²z² – 2bycz + c²y²) = 0

⇔ (ay – by)² + (az – cx)² + (bz – cy)² = 0

Vì (ay – bx)² ≥ 0; (az – cx)² ≥ 0; (bz – cy)² ≥ 0 nên

(ay – by)² + (az – cx)² + (bz – cy)² ≥ 0

Vậy dấu “=” xảy ra khi:

$\{\begin{cases} a y = b x \\ a z = c x \\ b z = c y \end{cases} \Rightarrow \{\begin{cases} \frac{a}{x} = \frac{b}{y} \\ \frac{a}{x} = \frac{c}{z} \\ \frac{b}{y} = \frac{c}{z} \end{cases}$