Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 103) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 103)
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm giao điểm I của AM và (SBD).
b) Tìm giao điểm P của SD và (ABM). Chứng minh rằng P là trung điểm của SD.
c) Gọi N là điểm tùy ý trên cạnh AB. Tìm giao điểm K của MN và (SBD).
Lời giải:
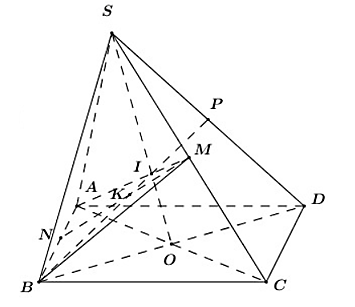
a) Trong (ABCD) gọi O = AC ∩ BD. Suy ra SO ⊂ (SAC), SO ⊂ (SBD)
Trong (SAC) gọi I = AM ∩ SO ta có:
I ∈ AM, I ∈ SO ⊂ (SBD)
Nên I ∈ (SBD)
Suy ra: I = AM ∩ (SBD)
b) Trong (SBD) gọi P = BI ∩ SD ta có:
P ∈ SD
P ∈ BI ⊂ (ABM) nên P ∈ (ABM)
Suy ra: P = SD ∩ (ABM)
Ta có: I là trọng tâm tam giác SAC nên SISO=23
Xét tam giác SBD có SO là trung tuyến ứng với cạnh BD, SISO=23
Nên I là trọng tâm tam giác SBD
Suy ra: BI là trung tuyến của tam giác SBD ứng với cạnh SD
Mà BI ∩ SD = P nên P là trung điểm của SD.
c) Trong (SBD) gọi K = MN ∩ BP ta có:
K ∈ MN
K ∈ BP ⊂ (SBD) nên K ∈ (SBD)
Vậy K = MN ∩ (SBD).
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K, J lần lượt là trọng tâm tam giác ABC và tam giác SBC. Xác định thiết diện hình chóp cắt bởi mặt phẳng chứa KI và song song AD.
Lời giải:
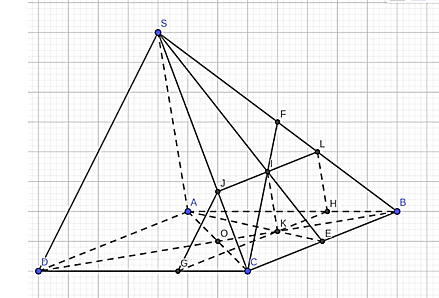
Ta dựng hình như hình vẽ.
Gọi GH // AD, G ∈ CD, H ∈ AB
JL // BC, I ∈ JL
Suy ra: GJLH là thiết diện cắt bởi mặt phẳng chứa KI và song song AD.
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ^BAD=120° , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.
Lời giải:
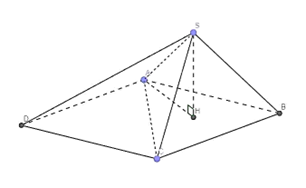
Ta có: ^BAD=120°⇒^ABC=60°
Suy ra: tam giác ABC đều
Gọi H là hình chiếu vuông góc của S lên (ABC)
Do SA = SB = SC nên HA = HB = HC
Suy ra: H trùng tâm đường tròn ngoại tiếp ABC
⇒ H là trọng tâm tam giác ABC (do tam giác đều)
⇒ AH=23.a√32=a√33
SH ⊥ (ABC) nên là góc giữa SA và đáy
Tức: ^SAH=60°
⇒ SH = AH.tan60°
VS.ABCD=13.SH.SABCD=13.a.2SABC=13.a.2.a2√34=a3√36.
Câu 4: Cho hình chóp S.ABCD có đáy là hình thang (AB//CD và AB = 3CD). Gọi H là điểm thuộc cạnh SC sao cho SH = 3HC. Gọi K là giao điểm của SB và (ADH). Tính tỉ số SKSB .
Lời giải:
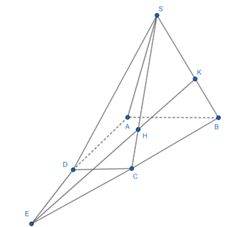
Chọn (SBC) ⊃ SB
Trong (ABCD), AD cắt BC tại E.
Từ đó ta có được (ADH) ∩ (SBC) = EH
Trong (SBC), EH ∩ SB = K
⇒ K = SB ∩ (ADH)
Áp dụng định lý Menelaus với ba điểm E, H, K thẳng hàng:
ECEB.BKKS.HSHC=1
Mà ECEB=DCAB=13;HSHC=3
Suy ra: BKKS=1⇒SKSB=12 .
Câu 5: Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại C, BC= a, ^BSC=60° cạnh SA vuông góc với đáy, mặt phẳng (SBC) tạo với (SAB) góc 30 độ. Thể tích khối chóp đã cho.
Lời giải:
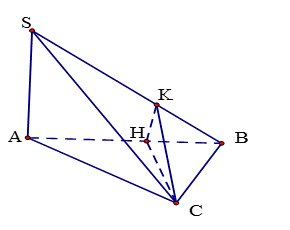
Từ C kẻ CH⊥AB tại H. Từ H kẻ HK⊥SB tại K.
+ Giao tuyến của hai mặt phẳng (SBC) và (SAB) là SB.
{HK∈(SAB)HK⊥SB
{CH⊥SBHK⊥SB⇒SB⊥CK
mà CK ∈ (SBC)
Do đó góc giữa hai mặt phẳng (SBC) và (SAB) là ^CKH=30°
{BC⊥ACBC⊥SA⇒BC⊥SC
Tam giác SBC vuông tại C có góc ^BSC=60° nên: SC=a√3;SB=2a√33
+ Tam giác SBC vuông tại C có CK là đường cao nên
1CK2=1CS2+1CB2=1a2+3a2=4a2
Suy ra: CK=a2
+ Tam giác CKH vuông tại H (vì CH⊥(SAB)) và ^CKH=30° nên: CH=CK.sin30°=a4
+ Tam giác ABC vuông tại C và có CH là đường cao nên 1CH2=1CA2+1CB2⇒1CA2=1CH2−1CB2=16a2−1a2=15a2
Suy ra: AC=a√15
+ Tam giác ABC vuông tại C nên AB=√AC2+BC2=4a√15
+ Tam giác SAB vuông tại nên SA=√SB2−AB2=√4a23−16a215=2a√15
Thể tích khối chóp là V=13.SA.SABC=16.SA.AC.BC=16.2a√15.a√15.a=a345.
Câu 6: Cho hình chóp S. ABC. Gọi M, N lần lượt là trung điểm của AC, BC, H, K lần lượt là trọng tâm của tam giác SAC, SBC.
a, Chứng mình AB// (SMK), HK// (SAB).
b, Tìm giao tuyến của hai mặt phẳng (CHK) và (ABC).
c, Tìm thiết diện của hình chóp với (P) đi qua MN và (P) // SC. Thiết diện là hình gì?
Lời giải:
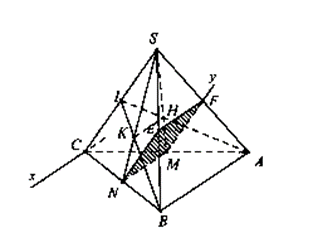
a) Ta có: AB // MN ⊂ (SMN)
AB ∉ (SMN)
Nên AB // (SMN)
Gọi I là trung điểm SC
Ta có: IHIA=13=IKIB
Mà HK, AB ⊂ (IAB) nên HK // AB ⊂ (SAB)
Và HK ∉ (SAB) nên HK // (SAB)
b) Ta có: C ∈ (CHK) ∩ (ABC) và (CHK) ⊃ HK // AB ⊂ (ABC) nên (CHK) ∩ (ABC) = Cx // AB // HK.
c) M ∈ (P) ∩ (SAC)
(P) // SC ⊂ (SAC)
Nên: (P) ∩ (SAC) = My // SC, gọi F = My ∩ SA
N ∈ (P) ∩ (SBC)
(P) // SC ⊂ (SBC)
Nên: (P) ∩ (SAC) = Nz // SC, gọi E = Nz ∩ SB
Khi đó ta được:
(P) ∩ (ABC) = MN; (P) ∩ (SBC) = NE; (P) ∩ (SAB) = EF; (P) ∩ (SAC) = FM
Vậy thiết diện cần tìm là tứ giác MNEF
Ta có: NE // MF mặt khác (P) ∩ (ABC) = MN; (P) ∩ (SAB) = EF, (ABC) ∩ (SAB) = AB
Mà AB // MN nên AB // MN // EF
Vậy thiết diện MNEF là hình bình hành.
Câu 7: Cho hình chóp S.ABCD với ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên SA. Tìm giao điểm của đường thẳng và MC và (SBD).
Lời giải:
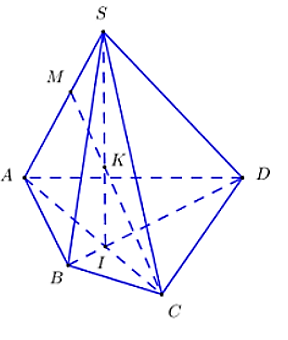
Trong (ABCD) gọi I = AC ∩ BD
Ta có: I ∈ AC ⊂ (SAC)
S ∈ (SAC)
Suy ra: SI ⊂ (SAC)
Trong (SAC) gọi K = SI ∩ MC ta có:
K ∈ MC
S ∈ SI ⊂ (SAC)
Suy ra: K = MC ∩ (SAC).
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.
a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).
b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.
Lời giải:
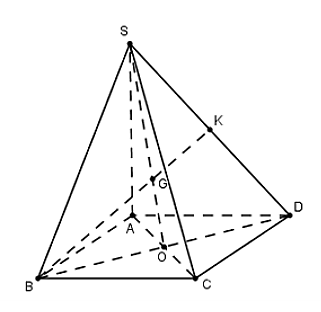
a) Gọi O = AC ∩ BD
⇒ O ∈ (SAC) ∩ (SBD) (1)
Mà S ∈ (SAC) ∩ (SBD) (2)
Từ (1) và (2) ⇒ (SAC) ∩ (SBD) = SO
b) Trong mặt phẳng (SBD) gọi G = BK∩SO
⇒ G ∈ SO ⊂ (SAC)
⇒ G = BK ∩ (SAC)
Ta có G = BK ∩ SO mà BK và SO là các đường trung tuyến của tam giác SBD
⇒ G là trọng tâm tam giác SBD.
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a; AD=a√3 . Hình chiếu S lên đáy là trung điểm H cạnh AB, góc tạo bởi SD và đáy là 60°. Tính thể tích V khối chóp S.ABCD.
Lời giải:
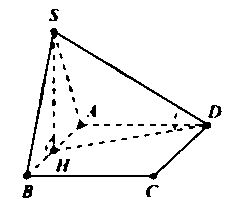
Vì HD là hình chiếu của SD lên mp(ABCD) nên (SD;(ABCD))=(SD,HD)=^SDH=60°
Tam giác AHD vuông tại A có: HD=√AH2+AD2=a√132
Tam giác SHD vuông tại H có: tan^SDH=SHHD⇒SH=HD.tan60°=a√392
VS.ABCD=13.SH.SABCD=13.a√392.a2√3=a3√132.
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA = a, SB=a√3 . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính khoảng cách từ điểm C đến mặt phẳng (SAD).
Lời giải:
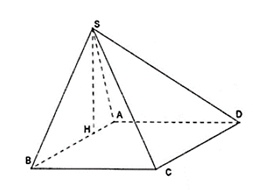
Gọi H là hình chiếu của S lên mp(ABCD)
Do (SAB) ⊥ (ABCD) nên SH là đường cao khối chóp
Ta có: OA = a, SB=a√3
Nên: SH=a√32;AH=a2
Ta có: d(C,(SAD))=3VS.ACDSSAD
VSACD=13.SH.SACD=a3√33; SSAD = a2
Suy ra: d(C,(SAD))=3VS.ACDSSAD=3.a3√33a2=a√3 .
Câu 10: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của cạnh SD, N thuộc cạnh SA sao cho NS = 2NA. Gọi I là giao điểm của mp (OMN) và cạnh CD. Tính ICID .
Lời giải:
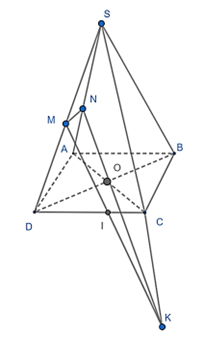
Chọn CD ⊂ (SCD)
Ta có M ∈ (OMN) ∩ (SCD)
Trong (SAC), kẻ ON cắt Sc tại K
Suy ra K ∈ SC ⊂ (SCD)
⇒ K ∈ (SCD) ∩ (OMN)
Ta được: MK = (OMN) ∩ (SCD)
Trong (SCD), MK ∩ CD = I
⇒ I = (OMN) ∩ CD
Áp dụng định lý Menelaus đối với △SCD cho 3 điểm K, M, I thẳng hàng ta được: ICID.DMMS.SKKC=1⇔ICID.1.SKKC=1⇔ICID=SKKC
Tiếp tục áp dụng định lý Menelaus cho △SAC với K, N, O thẳng hàng ta được: KSKC.COOA.NANS=1⇔KSKC.1.12=1⇔KSKC=ICID=12
(CO = AO do O là tâm hình bình hành ABCD).
Câu 11: Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của cạnh SC.
a) Chứng minh đường thẳng SA song song với nặt phẳng (MDB).
b) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB).
Lời giải:
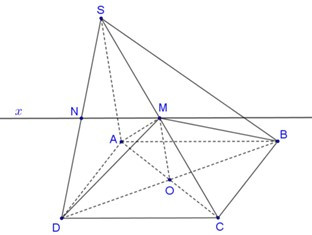
Xét ΔSAC, ta có:
M là trung điểm của SC
O là trung điểm của AC
Nên MO là đường trung bình của ΔSAC
Do đó SA // MO
Mà MO ⊂ (MDB)
Vậy SA // (MDB)
b) Tìm N = SD ∩ (MAB)
Chọn SD ⊂ (SCD)
{M ∈ SC, SC ⊂ (SCD); M ∈ (MAB)
⇒ M ∈ (SCD) ∩ (MAB)
{M ∈ (SCD) ∩ (MAB); CD // AB
⇒ (SCD) ∩ (MAB) = Mx // AB // CD
Gọi N = SD ∩ Mx
⇒ N = SD ∩ (MAB).
Câu 12: Cho hình chóp S.ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD; F là giao điểm của IK và SE; M là giao điểm của JK và BD. Tìm giao điểm của (IJK) và SD.
Lời giải:
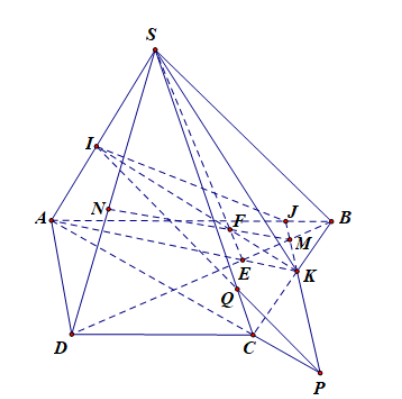
Chọn mp(SBD) chứa SD. Tìm giao tuyến của (SBD) và (IJK)
Có F = IK ∩ SE
Suy ra: {F∈IK⊂(IJK)F∈SE⊂(SBD)
Suy ra: F ∈ (IJK) ∩ (SBD) (1)
Trong mp(ABCD) gọi: M = JK ∩ BD
Suy ra: {M∈JK⊂(IJK)M∈BD⊂(SBD)
Suy ra: M ∈ (IJK) ∩ (SBD) (2)
Từ (1) và (2): MF là giao tuyến của (IJK) và (SBD)
Trong mp(SBD) gọi N = SD ∩ MF
⇒ {N∈SDN∈MF⊂(IJK)
⇒ N ∈ (IJK) ∩ SD
Vậy giao điểm của SD và (IJK) là giao điểm của SD và MF.
Câu 13: Cho hình chóp SABCD có đáy là hình thang với AD là đáy lớn, P thuộc SD. Gọi M, N là lần lượt trung điểm của AB, BC. Tìm thiết diện của hình chóp cắt bởi mặt phẳng MNP tứ diện này là hình gì?
Lời giải:
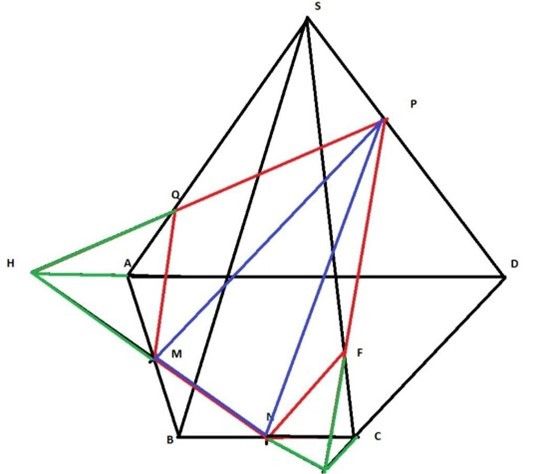
Gọi E là giao của MN và CD
H là giao của MN và AD
F là giao của PE và SC
Q là giao của PH và SA
Hình chóp cắt bới MNP tứ diện là hình ngũ giác QPFNM.
Câu 14: Cho chóp S.ABCD đáy là hình thang đáy lớn AD. Gọi I là trung điểm SA, J ∈ AD sao cho JD=14AD ; K ∈ SB : SK = 2BK. Tìm giao tuyến:
a) (IJK) và (ABCD).
b) (IJK) và (SBD).
c) (IJK) và (SBC).
Lời giải:
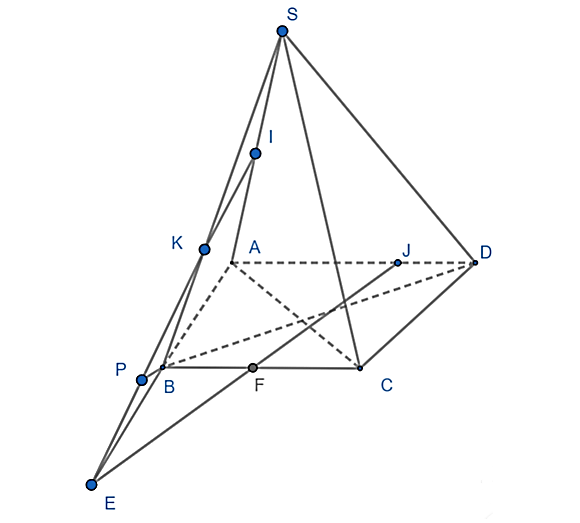
a) Trong (SAB) gọi E = IK ∩ AB
Ta thấy J thuộc AD, nên J ∈ (ABCD)
E ∈ AB nên E ∈ (ABCD)
Khi đó (IJK) ∩ (ABCD) = JE
b) Trong (ABCD) gọi P = IE ∩ BD
Khi đó P và K là 2 điểm chung của (IJK) và (SBD)
Suy ra: (IJK) ∩ (SBD) = KP
c) Gọi F = JE ∩ BC
Khi đó K và F là 2 điểm chung của (IJK) và (SBC)
Suy ra: (IJK) ∩ (SBC) = KF.
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Chứng minh đường thẳng OI song song với mặt phẳng (SAB) và mặt phẳng (SAD).
Lời giải:
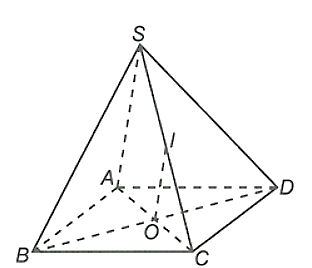
Ta có IO là đường trung bình của tam giác SAC suy ra IO // SA
Do SA ⊂ (SAB) và SA ⊂ (SAD)
Suy ra: IO // (SAB) và IO // (SAD).
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN / BS, NP // CD, MQ // CD. Hỏi PQ song song với mặt phẳng nào?
Lời giải:
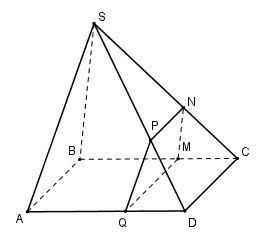
Vì MN // BS nên: CNCS=CMCB
Vì MQ // CD // AB nên: DQDA=CMCB
Vì NP // CD nên: CNCS=DPDS
Từ (1), (2), (3) suy ra:
Suy ra: PQ // SA
Mà SA ⊂ (SAB) và SA ⊂ (SAD)
Và PQ ⊂ (SAD)
Suy ra: PQ // (SAB).
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
Lời giải:
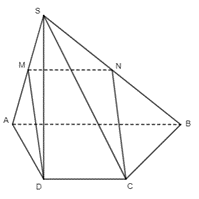
Trong mặt phẳng (SAB), có: M, N lần lượt là trung điểm của SA và SB
Do đó MN là đường trung bình của tam giác
Suy ra MN // AB và MN = 12AB
Lại có AB // CD (do ABCD là hình thang) và AB = 2CD hay CD = 12AB
Do đó MN // CD và MN = CD.
Suy ra MNCD là hình bình hành.
Vì vậy MD // NC.
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).
Lời giải:
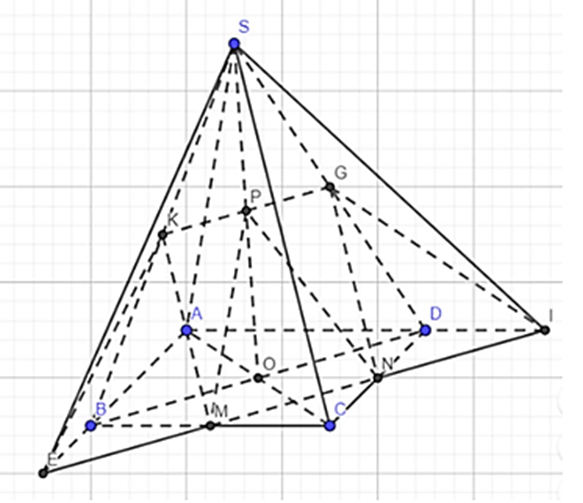
Gọi I, E lần lượt là giao điểm của MN với AD, AB
Qua P kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại K, G
Ta có:
M, N lần lượt là trung điểm của BC, CD ⇒ MN là đường trung bình của ∆BCD
⇒ MN // BD
Mà KG // BD ⇒ MN // KG ⇒ K, G ∈ (MNP)
Ta có:
{E=AB∩MN⇒E∈(SAB)∩(MNP)K∈SB,K∈(MNP)⇒K∈(SAB)∩(MNP)
{I=AD∩MN⇒I∈(SAD)∩(MNP)G∈SD,G∈(MNP)⇒G∈(SAD)∩(MNP)
{M,K∈(MNP)M,K∈(SBC)⇒(SBC)∩(MNP)=MK
{N,G∈(MNP)N,G∈(SCD)⇒(SCD)∩(MNP)=NG
Vậy (SAB) ∩ (MNP) = KE; (SAD) ∩ (MNP) = IG; (SBC) ∩ (MNP) = MK; (SCD) ∩ (MNP) = NG.
Câu 19: Cho hình chữ nhật ABCD có cạnh AD = a, M là trung điểm của cạnh AB. Biết rằng sin^MDB=13 . Tính độ dài của đoạn thẳng AB theo a.
Lời giải:
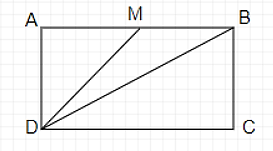
Ta có: sin^MDB=13⇒cos^MDB=√1−19=2√23(vì ^MDB<90° )
Lại có: SABD = SAMD + SBMD
⇔ 14a.AB+16.MD.DB=12.a.AB(1)
Xét tam giác MDB có: MB2 = MD2 + DB2 – 2.MD.DB.cos^MDB
⇔ AB24=MD2+DB2−2.MD.DB.2√23
⇔ MD.DB=(2a2+AB2).34√2(2)
Thế (2) vào (1) ta được: 4√2(2a2+AB2)=16.a.AB
⇔ AB2−2√2.a.AB+2a2=0
⇔ (AB−√2a)2=0
Suy ra: AB=a√2 .
Câu 20: Cho hình chữ nhật ABCD, kẻ BH vuông góc với AC. Trên AC, CD ta lấy các điểm M, N sao cho AMAH=DNDC . Chứng minh bốn điểm M, B, C, N nằm trên một đường tròn.
Lời giải:
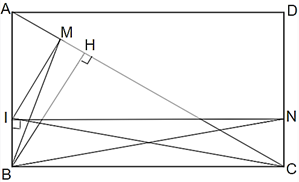
Kẻ NI // BC
Ta có: DNDC=AIAB=AMAH
Suy ra: MI // BH
⇒ ^IMB=^MBH(1)
Tứ giác IBCN có: ^IBC=^BIN=^BCN
⇒ Tứ giác IBCN là hình chữ nhật
⇒ ^NBC=^BCI(2)
Xét tứ giác IMCB có
^IMC=90°(vì IM // BH và BH vuông góc AC)
^IBC=90°
⇒ Tứ giác IMCB là tứ giác nội tiếp đường tròn
⇒ ^IMB=^ICB(3) (cùng chắn cung IB)
Từ (1), (2), (3) ⇒ ^MBH=^NBC
⇒ ^BMC=90°−^MBH=90°−^NBC=^CNB
⇒Tứ giác MBCN nội tiếp đường tròn
Hay M, B, C, N cùng nằm trên một đường tròn.
Câu 21: Cho hình chữ nhật ABCD. Điểm E nằm ngoài hình chữ nhật sao cho ^AEC=90°.Chứng minh rằng ^BED=90°.
Lời giải:
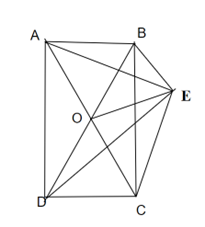
Gọi O là giao điểm của hai đường chéo AC và BD
Nên O là trung điểm của AC và BD
Tam giác ABC vuông tại A có AH là đường trung tuyến ứng với cạnh huyền AC
⇒ EO=12AC=12BD (vì AC = BD)
Xét tam giác BED có trung tuyến EO=12BD
⇒ Tam giác BED vuông tại E
⇒ ^BED=90°.
Câu 22: Cho hình chữ nhật ABCD. H là hình chiếu của B trên AC. M; K theo thứ tự là trung điểm của AH và CD. I và O lần lượt là trung điểm của AB và IC. Chứng minh:
a) MO=12IC .
b) ^BMK=90° .
Lời giải:
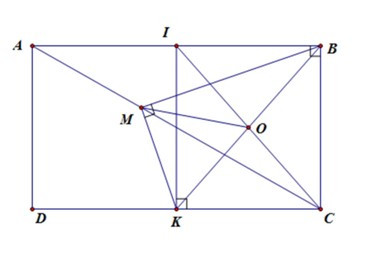
a) Trong tam giác AHB có MI đường trung bình (vì I và M là trung điểm AB và AH)
nên MI // HB
vậy IM vuông góc AC suy ra tam giác IMC vuông tại M.
Trong tam giác vuông IMC có MO trung tuyến ứng cạnh huyền IC nên MO=12IC
b) Ta có IBCK là hình chữ nhật (vì có IB = CK và IB // CK và có ˆB=ˆC=90° )
Nên IC = BK và O là trung điểm BK vì là giao điểm hai đường chéo của hình chữ nhật)
Mà MO=12IC nên MO=12BK .
Xét trong tam giác MKB có MO trung tuyến và MO=12BK
Nên tam giác MKB vuông tại M suy ra ^BMK=90° .
Câu 23: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, BC = 2, AA' = 2. Khoảng cách giữa hai đường thẳng AD' và DC' bằng? (tham khảo hình)
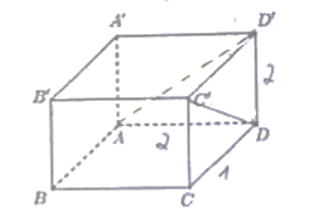
Lời giải:
AD' // (BC'D)
⇒ d(AD',C'D) = d(AD',(BC'D)) = d(A,(BC'D)) = d(C,(BC'D))
Kẻ CH ⊥ BD ⇒ BD⊥(C'CH)
Kẻ CK ⊥ C'H ⇒CK⊥(BC'D)
⇒ d(C,(BC'D)) = CK
Ta có: 1CH2=1BC2+1CD2⇒CH=2√55
1CK2=1CH2+1C'.
Câu 24: Cho hình hộp đứng ABCD.A'B'C'D', AB = AD = a, . Gọi M, N lần lượt là trung điểm của các cạnh A'D' và A'B'. Tính thể tích khối chóp A.BDMN.
Lời giải:
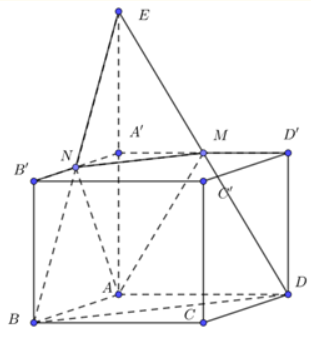
Vì AD = 2A’M nên BD = 2AM (theo định lý Ta-lét)
Nên hai tam giác EMN và EBD đồng dạng với nhau theo tỉ số 0,5 nên:
Ta có:
Câu 25: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45°. Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
Lời giải:
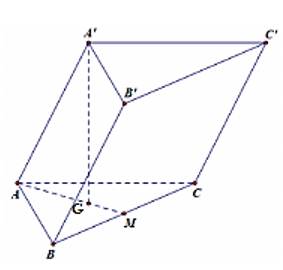
Gọi G là trọng tâm tam giác BAC
Do tam giác ABC đều cạnh a nên:
Do A’ cách đều ba đỉnh A, B, C nên A’G vuông góc (ABC)
Suy ra: A’G là đường cao của khối lăng trụ
Theo giả thiết ta có:
Suy ra: tam giác A’GA vuông cân
Từ đó suy ra:
Vậy thể tích khối lăng trụ là: .
Câu 26: Cho hình lăng trụ đứng tam giác ABC.A'B'C' có cạnh A B' = 3 cm, BC = 5 cm, AC' = 6 cm, AA' = 7 cm. Độ dài cạnh BC bằng
A. 3 cm.
B. 5 cm.
C. 6 cm.
D. 7 cm.
Lời giải:
Chọn B
Để tính độ dài cạnh BC của hình lăng trụ đứng tam giác ABC.A'B'C', ta sử dụng định lý Pythagore trong tam giác vuông ABB'.
Áp dụng định lí Pythagore vào ΔABC vuông tại B, ta có:
BC² = AB² + AC²
BC² = 3² + 4²
BC² = 9 + 16
BC² = 25
⇒ BC = 5 (cm).
Câu 27: Cho hình thang ABCD (AB // CD) có , AB = 4cm, AD = 6cm.
a) Tính đường cao AH của hình thang.
b) Tính BC.
c) Tính chu vi hinh thang ABCD.
Lời giải:
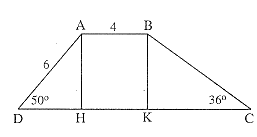
a) Vẽ AH vuông góc CD, BK vuông góc CD
Ta có: AHKB là hình chữ nhật vì
Suy ra: AH = BK, HK = AB = 4cm
Xét tam giác ADH vuông tại H, ta có: DH = AD.cosD = 6.cos50° = 3,9 (cm)
AH = AD.sinD = 6.sin50° = 4,6 (cm)
b) Xét tam giác BKC vuông tại K ta có: KC = BK.cotC = 4,6.cot36° = 6,3 (cm)
c) DC = DH + HK + KC = 3,9 + 4 + 6,3 = 14,2 (cm)
Do đó chu vi hình thang là: 4 + 7,8 + 14,2 + 6 = 32 (cm).
Câu 28: Hình thang ABCD (AB // CD) có AD = 15 cm; AC = 12 cm và CD = 13cm. Biết diện tích hình thang là 45 cm2. Tính chiều cao hình thang.
Lời giải:
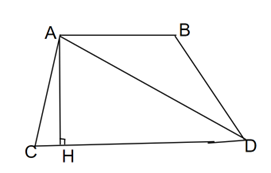
Kẻ đường cao AH
Đặt DH = x, CH = 13 – x
Theo định lý Pytago ta có:
152 – x2 = AH2 = 122 – (13 – x)2
⇔ 225 – x2 = 144 – 169 + 26x – x2
⇔ 250 = 26x
⇔
Suy ra: .
Câu 29: Hình thang ABCD (AB // CD) có . Tính các góc của hình thang.
Lời giải:
Vì ABCD là hình thang nên tổng 2 góc kề bằng 180 độ
Suy ra:
Suy ra:
Lại có:
Mà nên
Suy ra: .
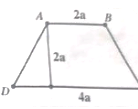
Câu 30: Cho hình thang ABCD như hình bên. Tìm a biết diện tích hình thang là 150cm2.
Lời giải:
Ta có: (2a + 4a).2a : 2 = 150
⇔ 6a.2a = 150.2
⇔ 12a2 = 300
⇔ a2 = 25
⇔ a = 5
Vậy a = 5cm.
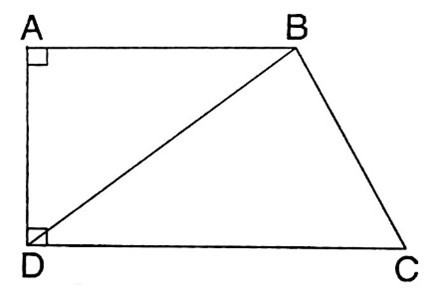
Câu 31: Cho hình thang vuông có đáy AB = a, CD = 2a đường cao AD = a. Xác định .
Lời giải:
Câu 32: Cho hình thang cân ABCD có CD = 2AB = 12cm, chu vi tam giác ACD là 25cm. Chu vi tam giác ABC là ...cm.
Lời giải:
Ta có: 2AB = 12 ⇒ AB = 6
ABCD là hình thang cân ⇒ BC = AD
PACD = 25 ⇒ AC + CD + DA = 25 ⇒ AC + AD = 25 – CD = 25 – 12 = 13
Suy ra: AC + BC = 13.
⇒ PABC = AB + BC + CA = 6 + 13 = 19.
Câu 33: Cho hình thang cân ABCD với cạnh đáy là AB và CD. Biết BD = 6cm, BC = 4cm. Tính AC, AD.
Lời giải:
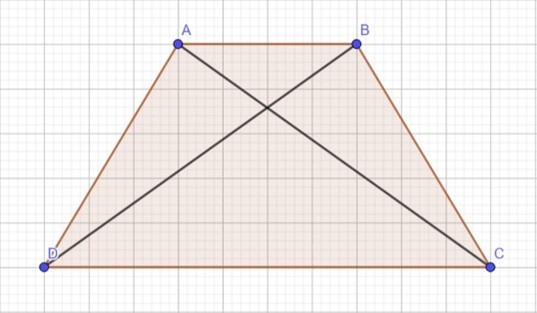
Vì ABCD là hình thang cân nên BD = AC = 6cm
BC = AD = 4cm.
Câu 34: Cho hình thang cân ABCD (AB // CD, AB < CD), BC = 15cm, đường cao BH = 12cm, DH = 16cm. Chứng minh BD vuông góc với BC.
Lời giải:
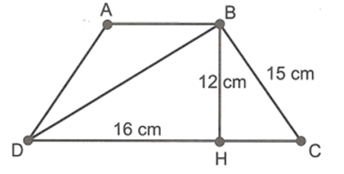
Áp dụng định lý Pitago cho tam giác BHD ta có:
BD2 = DH2 + BH2 = 162 + 122 ⇒ BD = 20.
Áp dụng định lý Pitago cho tam giác vuông BHC ta có:
HC2 = BC2− BH2 = 152 − 122 ⇒ HC = 9.
Tam giác BDC có BD2 + BC2 = 202 + 152 = 625;
DC2 = (16 + 9)2 = 625.
Suy ra BD2 + BC2 = DC2.
Từ đó theo định lý Pitago đảo, tam giác DBC vuông tại B, hay DB ⊥ BC.
Câu 35: Cho hình thang MNPQ (MN // PQ), có MP = NQ. Qua N kẻ đường thắng song song với MP, cắt đường thẳng PQ tại K. Chứng minh:
a) MNPQ là hình thang cân.
b) ∆MPQ = ∆NQP.
c) Tam giác NKQ cân.
Lời giải:
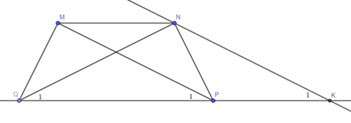
a) Hình thang MNPQ có MP = NQ (gt)
⇒ Hình thang MNPQ là hình thang cân (do hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân)
b) Hình thang MNPQ là hình thang cân
⇒ MQ = NP (do trong hình thang cân thì hai cạnh bên bằng nhau.)
Xét ΔMPQ và ΔNQP có
MQ = NP (cmt)
MP = NQ (gt)
PQ: chung
⇒ ΔMPQ = ΔNQP (c.c.c)
c) Ta có: ΔMPQ = ΔNQP (cmt)
⇒ (1) ( 2 góc tương ứng)
Mà NK // MP
⇒ ( 2 góc đồng vị) (2)
Từ (1) và (2) ⇒
⇒ ΔNQK cân tại N.
Câu 36: Cho hình thang vuông ABCD () cạnh , gọi H là hình chiếu của D lên AC. M, N là trung điểm của HC và HD.
a) Tứ giác ABMN là hình gì?
b) Chứng minh: = 90°.
Lời giải:
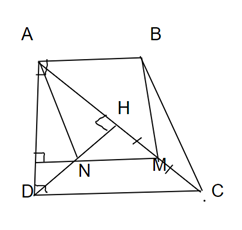
a) Tứ giác ABMN là hình bình hành vì:
+) MN // AB // DC do MN là đường trung bình của tam giác HDC nên MN // DC mà DC // AB
+) Và
Mà nên MN = AB.
b) Để chứng minh , ta sẽ sử dụng tính chất của hình thang vuông và hình chiếu.
Xét tam giác ADM có: DH vuông góc AM (giả thiết)
MN // DC và DC ⊥ AD nên MN ⊥ AD
Xét trong tam giác ADM có: MN ⊥ AD và DH ⊥ AM
Nên N là trực tâm của tam giác ADM
Suy ra: AN ⊥ DM
Gọi E là hình chiếu của B lên AC. Ta có:
Tam giác ABC vuông tại B, ta có BE là đường cao, do đó AE = EC.
Tam giác ACD vuông tại D, ta có DH là đường cao, do đó AH = HC.
Vì CD = 2AB và AE = EC, ta có:
AC = AE + EC = 2AB + AB = 3AB.
Lại có: AH = HC
Vậy, ta có AM = MN = ND = DH = AB.
Vậy, ta có AM = MN = ND = DH = AB.
Ta có tứ giác ABMN là tứ giác cân, với AM = MN và BM = ND.
Vì AM = MN = ND = DH = AB, nên ABMN là hình vuông.
Vậy .
Câu 37: Cho hình thoi ABCD có BC = 5cm. Chu vi hình thoi ABCD là:
A. 25 cm.
B. 20 cm.
C. 10 cm.
D. 25 cm.
Lời giải:
Chọn B.
Vì hình thoi có 4 cạnh bằng nhau nên BC = AD = AB = CD = 5cm.
Chu vi hình thoi = AB + BC + CD + DA = 5.4 = 20 (cm).
Câu 38: Cho hình thoi ABCD có cạnh bằng a, . Tính .
Lời giải:
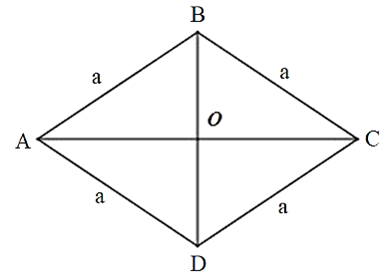
Gọi O là giao điểm 2 đường chéo AC và BD
Tam giác ABD có AB = AD và nên tam giác ABD đều
Suy ra: BD = a; OD =
Xét tam giác OCD vuông tại O
OC2 = CD2 – OD2 = .
Câu 39: Cho hình thoi ABCD có cạnh bằng a, O là tâm hình thoi, . Tính .
Lời giải:
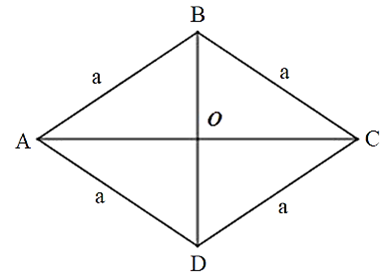
(vì AD = BC)
Lại có: Tam giác ABD cân tại A vì AB = AD nên AO là đường phân giác
Suy ra:
Xét tam giác AOB vuông tại O có:
Vậy .
Câu 40: Cho hình thoi ABCD có cạnh bằng a, . Tính diện tích hình thoi ABCD.
Lời giải:
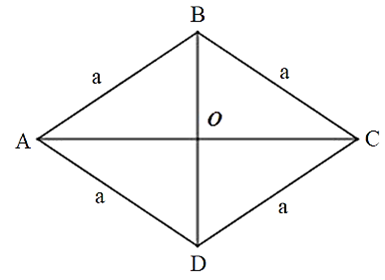
Ta có: .
Câu 41: Cho hình thoi ABCD, O là giao điểm hai đường chéo. Vẽ đường thẳng qua B song song AC, vẽ đường thẳng qua C song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì? Vì sao?
b) Chứng minh: AB = OK.
c) Tìm điều kiện của tứ giác ABCD để tứ giác OBKC là hình vuông.
Lời giải:
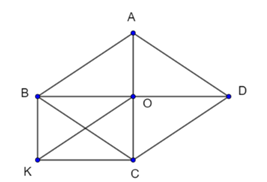
a) Xét hình thoi ABCD có AC và BD là hai đường chéo
Suy ra: AC vuông góc BD tại O ⇒
Ta có:
Tứ giác BOCK có:
Nên ONKC là hình chữ nhật.
b) Vì OBKC là hình chữ nhật (chứng minh câu a)
Nên BC = OK
Mà BC = AB (vì ABCD là hình thoi)
Suy ra AB = OK
Vậy AB = OK
c) OBKC là hình chữ nhật, do đó để OBKC là hình vuông thì OB = OC.
ABCD là hình thoi nên O là trung điểm của AC và BD.
⇒
Mà OB = OC nên AC = BD.
Do đó ABCD là hình vuông.
Vậy ABCD là hình vuông thì tứ giác OBKC là hình vuông.
Câu 42: Cho hình thoi ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh MNPQ là hình chữ nhật.
Lời giải:
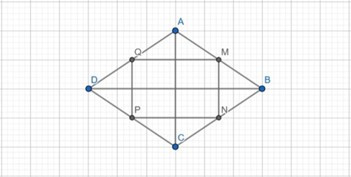
Xét △ABC:
M là trung điểm của AB (gt)
N là trung điểm của BC (gt)
⇒ MN là đường trung bình của △ABC
⇒ MN // AC,
Chứng minh tương tự
⇒ PQ // AC,
Xét tứ giác MNPQ:
MN // PQ (//AC)
MN = PQ
⇒ Tứ giác MNPQ là hình bình hành (2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Ta có: Tứ giác ABCD là hình thoi (gt)
⇒ AC ⊥ BD
Mà PQ // AC, NP // BD (cmt)
⇒ NP ⊥ PQ
⇒ Tứ giác MNPQ là hình chữ nhật.
Câu 43: Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm giao tuyến của (GMN) và (ACD).
Lời giải:
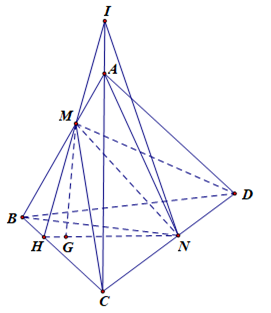
Có N ∈ CD ⊂ (ACD)
N ∈ (GMN)
Suy ra: N ∈ (ACD) ∩ (GMN) (1)
Trong mp(BCD) gọi H là giao điểm của NG và BC
Trong mp(ABC) gọi I là giao điểm AC và HM
Suy ra: I ∈ CA ⊂ (ACD)
I ∈ HM ⊂ (GMN)
Suy ra: I ∈ (ACD) ∩ (GMN) (2)
Từ (1) và (2) suy ra giao tuyến của (CAD) và (GMN) là NI.
Câu 44: Cho hình vẽ sau:
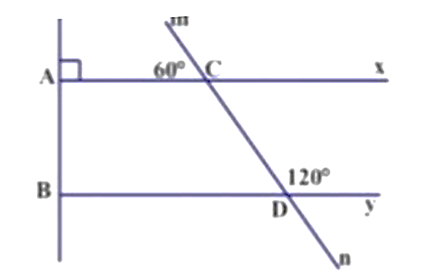
a) Tính số đo .
b) Chứng tỏ hai tia Ax và By song song.
c) Chứng tỏ By vuông góc với AB.
Lời giải:
a) Ta có: (2 góc đối đỉnh)
b) Ta có:
Mà 2 góc này ở vị trí trong cùng phía
Nên Ax // By
c) Vì Ax ⊥ AB, Ax // By nên By ⊥ AB.
Câu 45: Cho hình vẽ:
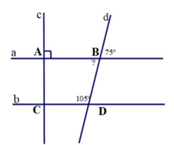
a) Tính số đo .
b) Chứng minh a // b.
c) Chứng minh c ⊥ b.
Lời giải:
a) (đối đỉnh với góc 75°)
b) Ta có: (2 góc trong cùng phía bù nhau)
Nên: a // b
c) Vì a // b và a ⊥ c nên c ⊥ b (quan hệ giữa tính vuông góc và song song).
Câu 46: Cho hình vẽ. Biết AB // CD, CD // EG. . Tính .
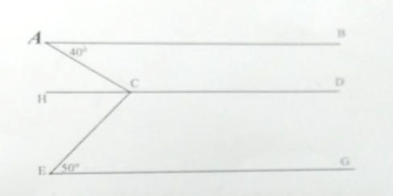
Lời giải:
Vì AB // CD nên: (trong cùng phía)
Nên:
AB // CD nên: (so le trong)
GE // CD nên: (so le trong)
Ta có: .
Câu 47: Cho tam giác ABC. Gọi M là trung điểm BC và I là trung điểm AM. Chứng minh rằng .
Lời giải:
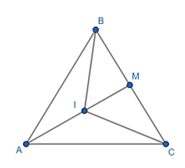
Vì I là trung điểm MA nên:
M là trung điểm của BC nên:
Vậy .
Câu 48: Cho hình vuông ABCD có AB = 4, gọi E là trung điểm của cạnh CD và F là điểm thuộc cạnh AC sao cho CF= 3AF. Tính độ dài cạnh EF.
Lời giải:
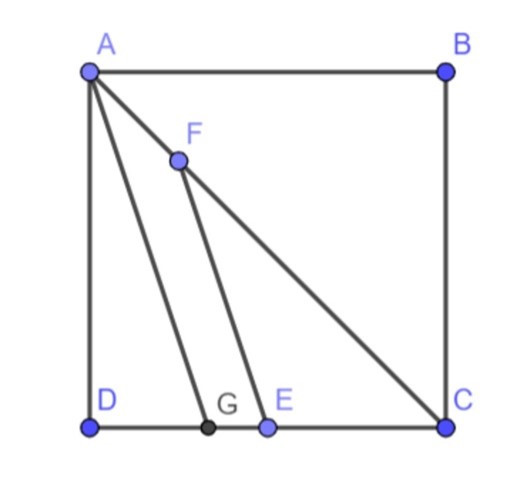
Kẻ AG // EF (G ∈ DC)
ABCD là hình vuông ⇒ AB = AC = BC = CD = 4
ΔCAG, FE // AG nên
⇒
DG = CD – DG =
ΔADG vuông tại D (do ABCD là hình vuông)
Nên:
.
Câu 49: Cho hình vuông ABCD cạnh a có O là giao điểm của 2 đường chéo. Tính .
Lời giải:
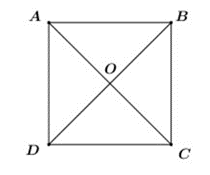
.
Câu 50: Cho hình vuông ABCD có cạnh là a. Trên cạnh BC lấy điểm E, đường thẳng AE cắt đường thẳng CD tại điểm M. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh .
Lời giải:
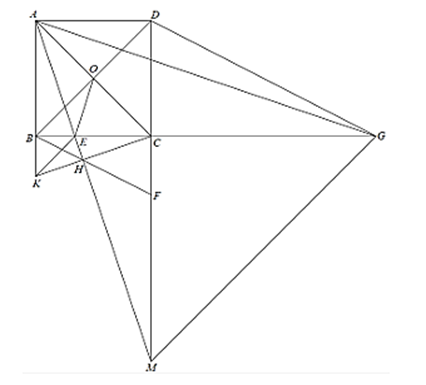
Xét tam giác AEB và tam giác MAD có:
(so le trong)
Vậy nên ΔAEB ∽ ΔMAD(g.g)
⇒
⇒ AE.DA = AM.BE
⇒ AE2.a2 = MA2.BE2
⇒ AE2.a2 = MA2(AE2 – AB2) = MA2.AE2 – MA2.AB2
⇒ AE2.a2 + MA2.AB2 = MA2.AE2
a2(AE2 + MA2) = MA2.AE2
⇒ .
Câu 51: Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND tính .
Lời giải:
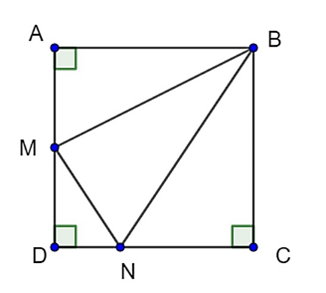
Giả sử cạnh của hình vuông ABCD là a
Suy ra: AB = BC = CD = DA = a
M là trung điểm AD ⇒ AM = MD =
NC = 2ND; NC + ND = CD = a
Suy ra:
Tam giác ABM vuông tại A có:
Tam giác DMN vuông tại D có:
Lại có:
Suy ra: .
Câu 52: Cho hình vuông ABCD và CDIS không thuộc mặt phẳng và cạnh bằng 4. biết tam giác SAC cân tại S, SB = 8. Thiết diện của mp ACI và hình chóp ABCD có diện tích bao nhiêu?
Lời giải:
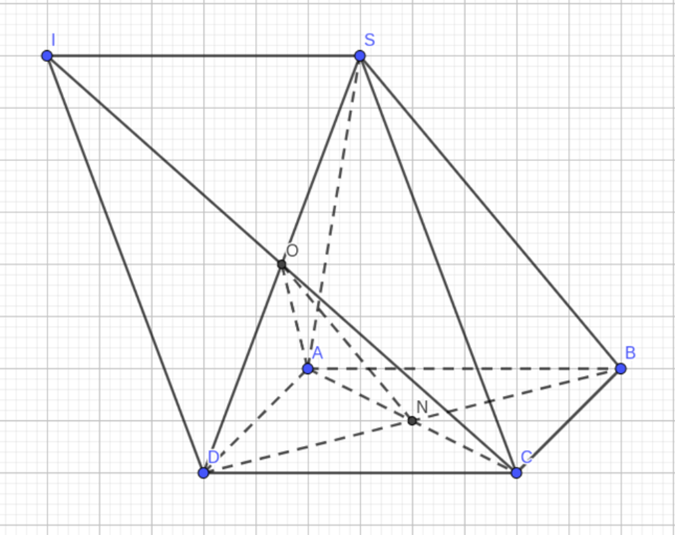
Gọi SD ∩ CI = O, AC ∩ BD = N
Suy ra: O, N là trung điểm SD, DB
ON =
(ACI) ∩ (S.ABCD) = (OCA)
Vì tam giác SAC cân tại S nên SC = SA
Xét tam giác SDC và tam giác SDA có:
Chung SD
SC = SA
DC = DA
Nên: ΔSDC = ΔSDA (c.c.c) ⇒ OA = OC
Suy ra: Tam giác OCA cân tại O
⇒
Câu 53: Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho ; N là trung điểm của đoạn thẳng DC. Chứng minh tam giác BMN vuông cân.
Lời giải:
Đặt
Do AB và AD vuông góc với nhau và AB = AD nên
Khi đó:
Ta có:
Mặt khác:
Vậy tam giác BMN vuông cân tại đỉnh M.
Câu 54: Cho hàm số y = (m – 3)x.
a) Với giá trị nào của m thì hàm số đồng biến.
b) Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1; 2).
Lời giải:
Điều kiện: m – 3 ≠ 0 ⇔ m ≠ 3
a) Để hàm số đồng biến thì m – 3 > 0 hay m > 3.
b) Đồ thị của hàm số y = (m – 3)x đi qua điểm A(1; 2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2 = (m – 3).1 ⇔ 2 = m – 3 ⇔ m = 5
Giá trị m = 5 thỏa mãn điều kiện bài toán.
Vậy với m = 5 thì đồ thị hàm sô y = (m – 3)x đi qua điểm A(1; 2).
Câu 55: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, SA = SB = SC = AC = a, SB tạo với mặt phẳng (SAC) một góc 30°. Tính thể tích khối chóp.
Lời giải:
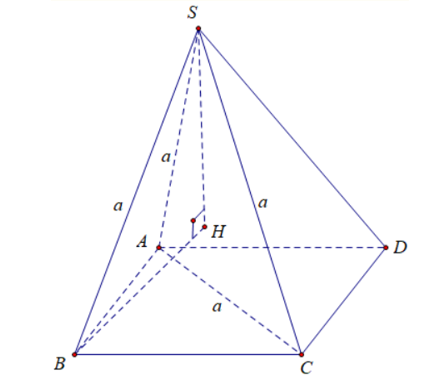
Vẽ BH vuông góc (SAC) tại H
(SB, (SAC)) = (SB, BH) =
Từ đó ta có: VS.ABCD = 2.VS.ABC = 2.VB.SAC
Xét tam giác SHB vuông tại H ta có:
Ta có:
Suy ra: .
Câu 56: Cho log615 = a; log1218 = b. Biểu diễn log2524 theo a và b.
Lời giải:
Từ (2) suy ra: b(2 + log23) = 1 + 2log23
⇔ (b – 2)log23 = 1 – b
⇔
Từ (1): log25 = a(a + log23) – log23 = (a – 1)log23 + a =
Suy ra: log2524 = .
Câu 57: Cho lục giác đều ABCDEF tâm O, xác định các vectơ
.
Lời giải:
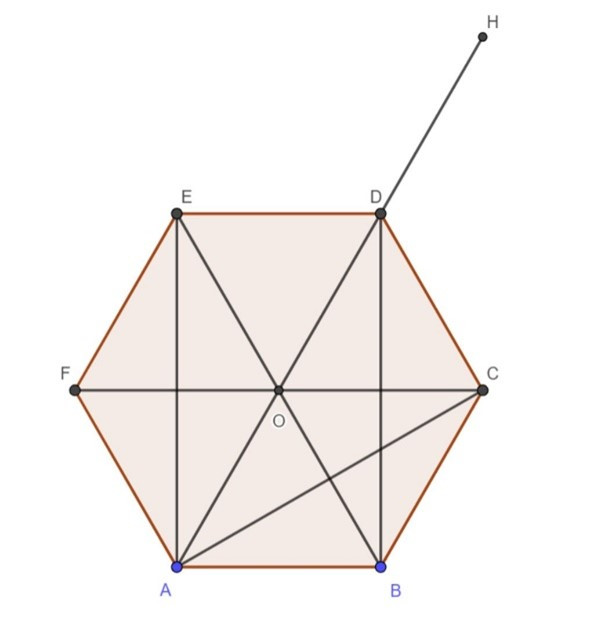
(với , cùng chiều ).
Câu 58: Cho P là 1 điểm bên trong hình chữ nhật ABCD sao cho PA = 3cm, PD = 4cm, PC = 5cm. Hãy tính độ dài đoạn thẳng PB?
Lời giải:
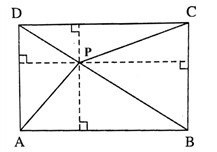
ABCD là hình chữ nhật ⇒ AD // BC
⇒
⇒
⇒
⇒ PB = 4 . 5 : 3 = 6,7 (cm).
Câu 59: Một phép chia có thương là 7 và số dư là 112. Biết tổng của số bị chia, số chia, thương và số dư là 1375. Tìm phép chia đó.
Lời giải:
Gọi số bị chia là a, số chia là b
Ta có: a = 7b + 112
Lại có: a + b + 7 = 1375
⇒ 7b + 112 + b = 1375 – 7 = 1368
⇒ b = (1368 - 112) : 8 = 157
⇒ a =7b + 112 = 7.157 + 112 = 1211
Suy ra phép chia cần tìm là 1211 : 157 = 7 dư 112.
Câu 60: Cho phương trình cos5x = 3m - 5. Đoạn [a; b] là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Tính 3a + b.
Lời giải:
Ta có: −1 ≤ cos5x ≤ 1 với mọi x
Để phương trình có nghiệm thì −1 ≤ 3m – 5 ≤ 1
⇔
Vậy
Suy ra: 3a + b = 6.
Câu 61: Tìm số nghiệm nguyên không âm, số nghiệm dương của phương trình x + y + z = 100.
Lời giải:
* Xét phương trình x + y + z = n (*)
Số nghiệm nguyên không âm của (*) tương đương với số nghiệm nguyên dương của x' + y' + z' = n + 3 là (bài toán chia kẹo Euler)
Ở đây n = 100 nên số nghiệm nguyên không âm là
* Xét bài toán chia kẹo Euler, ta có: Số nghiệm nguyên dương cần tìm của phương trình x1 + x2 + ⋯+ xt = k là số cách chia k chiếc kẹo cho t đứa trẻ sao cho ai cũng có kẹo.
Xếp k chiếc kẹo thành 1 hàng ngang
⇒ giữa chúng có k-1 chỗ trống. Số cách chia kẹo thỏa mãn điều kiện đề bài chính là số cách đặt t - 1 “vách ngăn” vào t - 1 chỗ trống trong số k - 1 chỗ trống nói trên.
⇒ có cách chia.
Với bài toán trên, ta có k = 100 và t = 3 nên số nghiệm nguyên dương là .
Câu 62: Cho phương trình x2 + 4x + 4a – a2 = 0. Tìm a để phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn x1 = x22 – 6.
Lời giải:
Δ′ = a2 − 4a + 4 = (a − 2)2
Để phương trình có 2 nghiệm phân biệt thì a ≠ 2.
Theo định lý Vi-ét và kết hợp đề bài ta có: .
⇔
⇔
Lại có: x1x2 = 4a – a2
Khi đó: –a2 + 4a – 5 = 0
⇔ .
Câu 63: Cho phương trình: x2 – 3x + 3m – 1 = 0. Tìm m để phương trình có nghiệm.
Lời giải:
Phương trình: x2 – 3x + 3m – 1 = 0
Δ = (-3)2 – 4.1(3m – 1) = 9 – 12m + 4 = 13 – 12m
Phương trình có nghiệm khi và chỉ khi Δ ≥ 0
⇔ 13 − 12m ≥ 0
⇔ .
Câu 64: Cho phương trình (3x + 2k – 5)(x – 3k + 1) = 0, trong đó k là một số. Tìm các giá trị của k sao cho một trong các nghiệm của phương trình là x = 1.
Lời giải:
Thay x = 1 vào phương trình (3x + 2k – 5)(x – 3k + 1) = 0, ta có:
(3.1 + 2k – 5)(1 – 3k + 1) = 0
⇔ (2k – 2)(2 – 3k) = 0
⇔ 2k – 2 = 0 hoặc 2 – 3k = 0
Nếu 2k – 2 = 0 ⇔ k = 1
Nếu 2 – 3k = 0 ⇔ k =
Vậy với k = 1 hoặc k = thì phương trình đã cho có nghiệm x = 1.
Câu 65: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K. Tính tỉ số .
Lời giải:
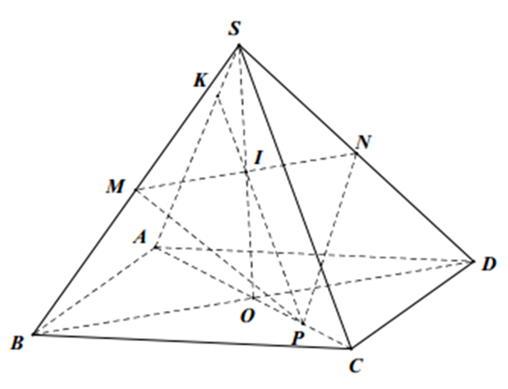
Trong mặt phẳng (SBD), gọi I là giao điêm của MN và SO
Ta có SA ⊂ (SAC); (MNP) ∩ (SAC) = PI
SA ⊂ (SAC); (MNP) ∩ (SAC) = PI
Trong mặt phẳng (SAC), PI cắt SA tại K ⇒ K là giao điểm của SA và (MNP)
Mặt khác: MN là đường trung bình của tam giác SBD nên MN cắt SO tại trung điểm I
⇒ PI là đường trung bình của tam giác ⇒ PI // SC hay PK // SC.
⇒ .
Câu 66: Cho sin α = và 90° < α < 180°. Tính giá trị của biểu thức .
Lời giải:
Ta luôn có: sin2 α + cos2 α = 1 nên cos2α = 1 - sin2 α =
Suy ra:
Vì 90° < α < 180° nên
.
Câu 67: Cho . Tính giá trị của sin2x.
Lời giải:
Vì sin2x + cos2x = 1 mà nên
Mà nên cosx > 0 do đó:
.
Câu 68: Cho và a, b là các góc nhọn. Tính A = sin(a – b).
Lời giải:
A = sin(a – b) = sina.cosb – sinb.cosa = .
Câu 69: Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện logax > logbx > logcx. So sánh a, b, c?
Lời giải:
logax > logbx > logcx
⇔ .
Câu 70: Cho tam giác ABC vuông tại A có . Tính tỉ số lượng giác góc .
Lời giải:
Vì tam giác BAC vuông tại A nên
Suy ra:
.
Câu 71: Cho tam giác ABC vuông tại A, các trung tuyến AD và BE vuông góc với nhau tại G. Biết cm, tính BC.
Lời giải:
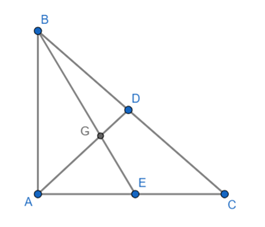
Xét tam giác BGA vuông tại G có:
BG2 + GA2 = AB
⇔
Lại có trong tam giác ABE thì AB2 + AE2 = BE2
⇔
Từ (1) và (2) ta có: BC2 + AC2 = 30 mà BC2 – AC2 = AB2 = 6
Nên BC2 = 18
Suy ra: .
Câu 72: Cho tam giác ABC biết AB = 50, BC = 70, . Tính gần đúng diện tích tam giác ABC.
Lời giải:
.
Câu 73: Cho tam giác ABC cân tại A; góc A = 120 độ và AB = AC = a. Tính .
Lời giải:
.
Câu 74: Cho tam giác ABC cân tại A đường trung trực của AB cắt BC tại K. Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp tam giác ACK.
Lời giải:
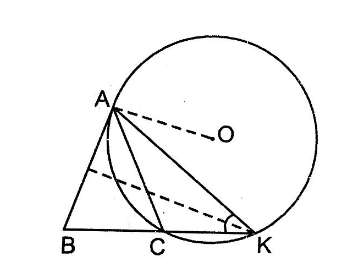
Các tam giác cân ABC, KBA có chung góc ở đáy B nên .
tức
Ta có
Suy ra:
Từ đó AB là tiếp tuyến của đường tròn (O).
Câu 75: Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC = 5a, BC = 6a. Tính khoảng cách từ điểm O đến dây BC theo a.
Lời giải:
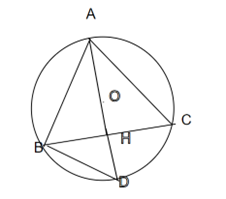
Kẻ đường kính AD sao cho A, O, D, H thẳng hàng
Vì ABC cân tại A nên AB = AC = 5a.
HB = HC = BC : 2 = 6a : 2 = 3a
Tam giác AHC vuông tại H, ta có:
Tam giác ABD nội tiếp đường tròn tâm O đường kính AD nên:
Suy ra: Tam giác ABD vuông tại B
Theo hệ thức lượng, ta có: AB2 = AH.AD
Suy ra: AD = 25a2 : 4a =
OA = OD =
Khoảng cách từ O đến BC = OH = AH – OA = .
Câu 76: Cho tam giác ABC cân tại A sao cho và . Ở phía ngoài tam giác ABC, dựng tam giác cân ADC sao cho . Tính .
Lời giải:
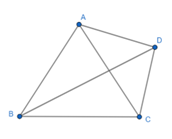
Vì tam giác ABC cân tại A nên:
Xét tam giác ADC có:
Suy ra:
⇒
Lại có:
Xét tứ giác ABCD có:
Suy ra tứ giác ABCD nội tiếp đường tròn
⇒ (góc nội tiếp cùng chắn cung ).
Câu 77: Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N.
a) Chứng minh rằng: DM = EN.
b) MN cắt BC tại I. Chứng minh I là trung điểm của MN.
Lời giải:
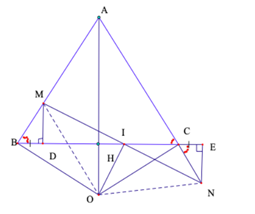
a) Xét ∆BDM và ∆CEN có:
BD = CE
Suy ra: ∆BDM = ∆CEN (g.c.g)
⇒ DM = EN
b) Xét ∆MDI và ∆NEI có:
DM = EN
(so le trong vì MD // NE)
Suy ra: ∆MDI = ∆NEI (g.c.g)
⇒ IM = IN
Vậy I là trung điểm MN.
Câu 78: Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, ta vẽ đường thẳng vuông góc với BC, cắt các cạnh AB, AC lần lượt tại E, F. Vẽ các hình chữ nhật BDEH, CDFK. Chứng minh rằng A là trung tâm điểm của HK.
Lời giải:
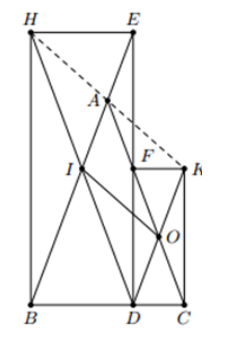
Gọi I, O lần lượt là tâm của BDEH, CDFK
Ta có:
Mà (do tam giác ABC cân tại A)
Nên:
Do đó: BE // DK, DH // CA
Suy ra: AIDO là hình bình hành
Nên: AO = ID
Mà HI = ID nên AO = HI
Lại có AO // HI và AIHO là hình bình hành nên AH // IO và AH = IO (1)
Chứng minh tương tự: AIOK là hình bình hành nên AK // io, AK = IO (2)
Từ (1) và (1): Suy ra: A, H, K thằng hàng và AH = AK.
Vậy A là trung điểm của HK.
Câu 79: Cho tam giác ABC, điểm M thuộc cạnh AB sao cho 3AM = AB và N là trung điểm của AC. Tính theo .
Lời giải:
Vì N là trung điểm AC nên:
⇔
Suy ra: .
Câu 80: Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Dựng đường tròn (K) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm F, E. Gọi H là giao điểm của BE và CF.
a) Chứng minh rằng AF.AB = AE.AC và AH vuông góc BC.
b) Chứng minh OA vuông góc EF.
Lời giải:
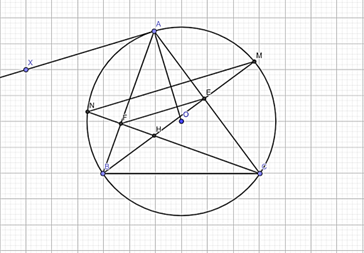
a) Ta có: (góc nội tiếp chắn nửa đường tròn (O))
Suy ra: BE, CF là hai đường cao của tam giác ABC
⇒ H là trực tâm của tam giác ABC
AH là đường cao của ABC nên AH ⊥ BC tại S
b) Vẽ tiếp tuyến Ax của (O)
Có: (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)
(vì cùng bù )
⇒ mà hai góc ở vị trí so le trong nên Ax // EF
Ta lại có OA ⊥ Ax (Ax là tiếp tuyến của (O)) ⇒ OA ⊥ EF.
Câu 81: Cho tam giác ABC có: . Chứng minh BC2 = BC.AC + AB2.
Lời giải:
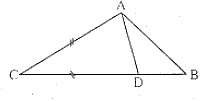
Theo giả thiết: nên
Nên góc A lớn nhất, cạnh BC lớn nhất trong tam giác ABC
Trên cạnh BC lấy điểm D sao cho CD = AC
Thay vào (1) ta có:
Suy ra: ∆CBA ∽ ∆ABD (g.g)
⇒
⇒ BC2 – BC.AC = AB2
⇒ BC2 = BC.AC + AB2.
Câu 82: Cho tam giác ABC có ; AB = 10cm.
a) Tính đường cao BH và cạnh BC.
b) Tính diện tích tam giác ABC.
Lời giải:
a)
AH =
Suy ra:
b) SABC = .
Câu 83: Cho tam giác ABC, AB = AC = a, góc A = 120°, lấy điểm M trên cạnh BC sao cho 5BM = 2BC. Tính độ dài đoạn AM?
Lời giải:
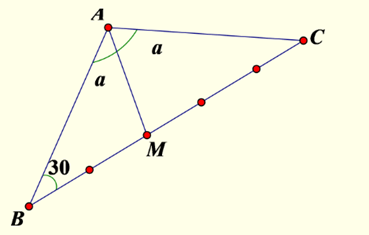
Suy ra:
Câu 84: Cho tam giác ABC có A(1;3), B(-1;-5), C(-4;-1). Viết phương trình đường cao AH của tam giác ABC.
Lời giải:
Gọi H(x; y)
Ta có:
Mà AH ⊥ BC nên:
Suy ra: (-3)(x – 1) + 4(y – 3) = 0
⇔ -3x + 4y – 9 = 0
Vậy phương trình AH là: -3x + 4y – 9 = 0.
Câu 85: Cho tam giác ABC có độ dài 3 cạnh: AB = 20 cm, AC = 34cm, BC = 42 cm. Diện tích của tam giác đó là bao nhiêu?
Lời giải:
Áp dụng công thức Hê-rông: với p là nửa chu vi.
Nửa chu vi tam giác ABC là: (20 + 34 + 42) : 2 = 48 (cm)
Diện tích tam giác ABC là: .
Câu 86: Cho tam giác ABC có AB = 3, BC = 5, AC = 6. Trên cạnh AB lấy điểm M sao cho BM = 2AM, trên cạnh BC lấy điểm K sao cho 3KB = 2KC. Tính MK.
Lời giải:
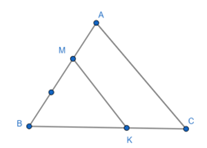
AB = 3; BM = 2AM nên
AM = 3 – 2 = 1
BC = 5;
Ta có:
Lại có: MK2 = BM2 + BK2 – 2BM.BK.cosB = 22 + 22 – 2.2.2.
Suy ra: .
Câu 87: cho tam giác ABC có AB = 12cm, AC=15cm. Trên cạn AB lấy M sao cho AM = 8cm, trên AC lấy N sao cho AN = 10cm. lấy D là điểm bất kì trên BC. AD cắt MN tại E. Tính tỉ số .
Lời giải:
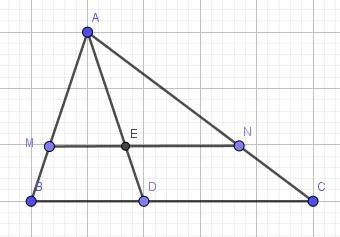
Ta có:
Xét trong tam giác ABC có:
Theo ta-lét đảo ta có: MN // BC
Lại có: ME // BC nên:
Vậy .
Câu 88: Cho ∆ABC có AB = 2, AC = 3, . Tính độ dài phân giác .
Lời giải:
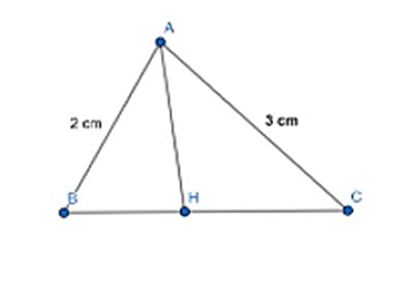
Áp dụng định lí hàm số côsin cho ∆ABC ta có:
BC2 = AB2 + AC2 - 2AB.AC.cos60
Suy ra: BC =
Gọi AH là đường phân giác góc A.
Áp dụng tính chất đường phân giác cho ∆ABC:
Xét tam giác ABH có: AH2 = AB2 + BH2 – 2.AB.BH.
Suy ra: .
Câu 89: Cho tam giác ABC có . Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC). Tính .
Lời giải:
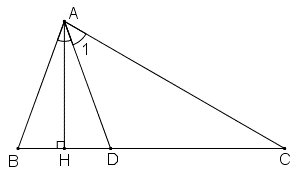
Vì nên
Ta có:
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có là góc ngoài tại đỉnh D
Do đó: (tính chất góc ngoài của tam giác).
Câu 90: Cho ΔABC có BC = 6, AB = 5, và . Tính độ dài trung tuyến BM và cosin của góc nhọn tạo bởi BM và đường cao AH.
Lời giải:
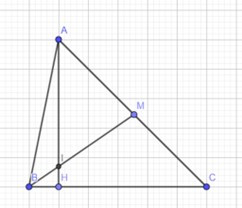
Áp dụng định lý cosin ta có:
Xét tam giác ABC có BM là trung tuyến
Suy ra:
Do nên nên ta có hình vẽ như trên
Gọi I là giao điểm của AH và BM
Suy ra:
Xét tam giác IBH có:
Suy ra:
Suy ra: .
Câu 91: Cho ΔABC cố định, các điểm D và E di động trên các cạnh tương ứng là AB và AC sao cho . Chứng minh rằng: Trung điểm M của đoạn thẳng DE nằm trên 1 đoạn thẳng cố định.
Lời giải:
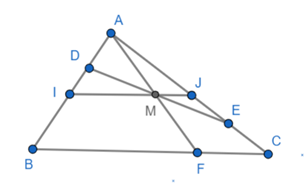
Ta có:
Từ E kẻ đường thẳng song song với AB cắt BC tại F (EF // BC)
Theo định lý ta-lét ta có:
Suy ra:
Lại có: EF // AB nên EF // AD
Suy ra: ADFE là hình bình hành
Mà ADFE là hình bình hành có M là trung điểm của đường chéo DE nên M cũng là trung điểm của AF
Gọi I, J lần lượt là trung điểm AB, AC
Suy ra: IJ là đường trung bình của tam giác ABC
⇒ IJ // BC (1)
Tam giác ABF có I là trung điểm AB, M là trung điểm AF nên IM là đường trung bình của tam giác ABF
⇒ IM // BC (2)
Từ (1) và (2): I, M, J thẳng hàng
Vậy M nằm trên IJ
Mà tam giác ABC cố định, nên IJ cố định, vậy M cố định.
Câu 92: Cho tam giác ABC có đường phân giác trong AD = 6, nó chia cạnh BC thành hai đoạn BD = 2, CD = 3. Tính AB, AC.
Lời giải:
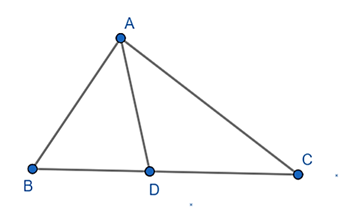
Áp dụng tính chất đường phân giác ta có: , suy ra: (*)
(vì AD là phân giác)
⇔
⇔
⇔ (**)
Thay (*) vào (**) ta được:
⇔
⇔
⇔
⇔
Suy ra: .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.