Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66)

Ngọc Nguyễn Ngày: 29-08-2023 Tổng hợp kiến thức

312

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) hay nhất được biên soạn và chọn lọc giúp bạn ôn luyện và đạt kết quả cao trong bài thi môn Toán.

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66)

Câu 1: Cho đa thức P(x) = x²+ bx + c, trong đó b và c là các số nguyên. Biết đa thức x⁴ + 6x² + 25 và đa thức 3x⁴ + 4x² + 28x + 5 đều chia hết cho P(x). Tính P(1).

Lời giải:

Theo bài ra, ta có: (x⁴ + 6x² + 25) ⋮ P(x) ⇔ 3(x⁴ + 6x² + 25) ⋮ P(x)

Lại có: (3x⁴ + 4x² + 28x + 5) ⋮ P(x)

Suy ra: [3(x⁴ + 6x² + 25) − (3x⁴ + 4x² + 28x + 5)] ⋮ P(x)

⇔ (3x⁴ + 18x² + 75 − 3x⁴ − 4x² − 28x – 5) ⋮ P(x)

⇔ (14x² − 28x + 70) ⋮ P(x)

⇔ 14(x² − 2x + 5) ⋮ P(x)

⇔ (x² − 2x + 5) ⋮ P(x)

Hay (x⁴ − 2x + 5) ⋮ (x² + bx + c)

Mà b, c là các số nguyên nên để (x⁴ − 2x + 5) ⋮ (x² + bx + c) thì: b = ‒2, c = 5.

Khi đó, P(1) = 12 − 2.1 + 5 = 1 − 2 + 5 = 4.

Vậy P(1) = 4.

Câu 2: So sánh 4³⁰ và 3.24¹⁰.

Lời giải:

Ta có:

4³⁰ = 2³⁰.2³⁰ = 2³⁰.(2²)¹⁵ = 2³⁰.4¹⁵ = 2³⁰.4¹¹.4⁴

3.24¹⁰ = 3.(3.2³)¹⁰ = 3.3¹⁰.2³⁰ = 3¹¹.2³⁰

Mà 4¹¹.4⁴ > 3¹¹ ⇒ 4³⁰ > 3.24¹⁰

Câu 3: Tìm số tự nhiên n để: n²⁰²¹ + n²⁰²⁰ + 1 là số nguyên tố.

Lời giải:

Ta có:

n²⁰²¹ + n²⁰²⁰ + 1

= n²⁰²¹ ‒ n² + n²⁰²⁰ ‒ n + n² + n +1

= n²(n²⁰¹⁹ ‒ 1) + n(n²⁰¹⁹ ‒ 1) + (n² + n +1)

= (n² + n)(n²⁰¹⁹ ‒ 1) + (n² + n +1)

= n(n + 1)(n²⁰¹⁹ ‒ 1) + (n² + n +1) (1)

Để ý rằng, 2019 chia hết cho 3 và 2019 = 3.673

Nên nếu đặt A = n³ thì n²⁰¹⁹ = A⁶⁷³

Mặt khác áp dụng hằng đẳng thức sau:

a^k ‒ b^k = (a ‒ b)(a^k‒1 + a^k‒2b¹ + a^k‒3b² +...+ a¹b^k‒2 + b^k‒1)

Ta có: n²⁰¹⁹ ‒ 1 = A⁶⁷³ ‒ 1 = A⁶⁷³ ‒ 1⁶⁷³ = (A ‒ 1)(A⁶⁷² + A⁶⁷¹ + ... + A¹ + 1)

⇒ n²⁰¹⁹ ‒ 1 ⋮ (A ‒ 1) hay n²⁰¹⁹ ‒ 1 ⋮ (n³ ‒ 1)

Mà n³ ‒ 1 = (n ‒ 1)(n² + n +1) ⇒ n²⁰¹⁹ ‒ 1 ⋮ (n² + n +1) (2)

Từ (1) và (2) ⇒ n²⁰²¹ + n²⁰²⁰ + 1 ⋮ (n² + n +1)

Như vậy để n²⁰²¹ + n²⁰²⁰ + 1 là một số nguyên tố thì có hai trường hợp:

1. n² + n +1 = 1, trường hợp này không xảy ra do n > 0 (giả thiết)

2. n²⁰²¹ + n²⁰²⁰ + 1 = n² + n +1 hay n²⁰²⁰(n + 1) = n(n + 1) ⇒ n(n + 1)(n²⁰¹⁹ ‒ 1) = 0

Do n > 0 nên n²⁰¹⁹ ‒ 1 = 0 ⇒ n = 1

Thử lại ta có: n²⁰²¹ + n²⁰²⁰ + 1 = 1²⁰²¹ + 1²⁰²⁰ + 1 = 3 là số nguyên tố.

Vậy n = 1 là đáp án cần tìm.

Câu 4: Tìm số nguyên tố p sao cho p + 8 và p + 16 đều là các số nguyên tố.

Lời giải:

Xét p = 2 ⇒ p + 8 = 2 + 8 = 10 (loại)

Xét p = 3 ⇒ p + 8 = 3 + 8 = 11 (tm)

p + 16 = 3 + 16 = 19 (tm)

Xét p là số nguyên tố và p > 3 ⇒ p = 3k + 1 hoặc p = 3k + 2

Với p = 3k + 1 ⇒ p + 8 = 3k + 1 + 8 = 3k + 9 = 3(k + 3) (loại)

Với p = 3k + 2 ⇒ p + 16 = 3k + 2 + 16 = 3k + 18 = 3(k + 6) (loại)

Vậy p = 3.

Câu 5: Tìm tất các giá trị thực của tham số m để phương trình (m – 2)x + m² – 3m +2 = 0 có tập nghiệm là ℝ.

Lời giải:

(m – 2)x + m² – 3m +2 = 0

⇔ (m – 2)x = −m² + 3m ‒ 2

Đề để phương trình (m – 2)x + m² – 3m + 2 = 0 có tập nghiệm là ℝ.

$\Leftrightarrow \{\begin{cases} m - 2 = 0 \\ m^{2} - 3 m + 2 = 0 \end{cases} \Leftrightarrow \{\begin{cases} m = 2 \\ [\begin{array}{l} m = 1 \\ m = 2 \end{array} \end{cases} \Leftrightarrow m = 2$

Vậy m = 2 phương trình (m – 2)x + m² – 3m +2 = 0 có tập nghiệm là ℝ.

Câu 6: Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9, hỏi lập được bao nhiêu số tự nhiên mỗi số có 4 chữ số khác nhau, và trong đó có bao nhiêu số mà chữ số đứng sau lớn hơn chữ số đứng trước.

Lời giải:

Vì chữ số cần lập có chữ số đứng sau lớn hơn chữ số đằng trước nên không có chữ số 0.

Chọn 4 chữ số khác nhau từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 có $C_{9}^{4} = 126$ cách chọn.

Ứng với mỗi cách chọn đó chỉ có duy nhất 1 cách xếp mà chữ số đứng sau lớn hơn chữ số đằng trước.

Vậy có $C_{9}^{4} = 126$ số tự nhiên thỏa mãn yêu cầu.

Câu 7: Từ các chữ số của tập hợp {0; 1; 2; 3; 4; 5}, có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau mà trong đó nhất thiết phải có mặt chữ số 0?

Lời giải:

Số cách đặt chữ số 0 là 4.

Số cách chọn số vào 4 vị trí còn lại là: $A_{5}^{4} = 120$ .

⇒ Số số lập thành là: 4.120 = 480 (số).

Câu 8: Từ các chữ số 1, 2, 3, 4, 5, 6. Có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau và nhất thiết phải có chữ số 1 và 5

Lời giải:

Số lập được nhất thiết phải có số 1 và số 5.

⇒ Để chọn 3 số còn lại có: $C_{3}^{4}$ cách chọn

Mỗi số lập được là 1 hoán vị của 5 số.

⇒ Số các số lập được là: $C_{3}^{4} .5 = 480$ số

Câu 9: Chứng minh rằng x⁵ ‒ x + 2 không là số chính phương với mọi x thuộc ℤ.

Lời giải:

Ta có:

x⁵ ‒ x + 2

= x(x⁴ ‒ 1) +2

= x(x⁴ ‒ x² + x² ‒ 1) + 2

= x(x² ‒ 1)(x² + 1) + 2

= x(x² ‒ x + x ‒ 1)(x² + 1) + 2

= x(x ‒ 1)(x + 1)(x² + 1) + 2

Nhận thấy x(x ‒ 1)(x + 1) là tích 3 số nguyên liên tiếp nên chia hết cho 3

⇒ x(x ‒ 1)(x + 1)(x² + 1) + 2 chia 3 dư 2, không là số chính phương

Vậy x⁵ ‒ x + 2 không là số chính phương với mọi x thuộc ℤ

Câu 10: Xác định tham số m để hàm số y = f(x) = 3msin4x + cos2x là hàm số chẵn.

Lời giải:

TXĐ: D = ℝ

⇒ ∀ x ∈ D ⇒ ‒x ∈ D

Ta có:

$f (- x) = 3 m \sin (- 4 x) + \cos (- 2 x) = - 3 m \sin (4 x) + \cos (2 x)$

Để hàm số đã cho là hàm số chẵn thì:

f(‒x), = f(x), ∀ x ∈ D

⇔ 3msin4x + cos2x = ‒3m sin4x + cos2x, ∀ x ∈ D

⇔ 6msin4x = 0, ∀ x ∈ D

⇔ m = 0.

Câu 11: 5 phút bằng một phần mấy của giờ?

Lời giải:

1 giờ = 60 phút

⇒ 5 phút = $\frac{5}{60}$ giờ $= \frac{1}{12}$ giờ

Câu 12: Cho tam giác ABC có E là trung điểm của AC. Qua E kẻ ED // AB (D thuộc BC), EF // BC (F thuộc AB) cho tam giác ABC có E là trung điểm của AC. Chứng minh rằng tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.

Lời giải:

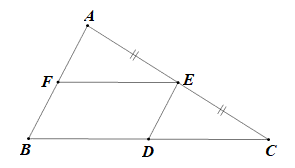
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 1)

Xét ΔABC có: E là trung điểm của AC và ED // AB

Do đó: D là trung điểm của BC.

Xét ΔABC có: E là trung điểm của AC và EF // BC

Do đó: F là trung điểm của AB.

Xét ΔABC có: F, E lần lượt là trung điểm của AB, AC

Do đó: FE là đường trung bình của ΔBAC.

⇒ FE // BD và FE = BD

Suy ra FEDB là hình bình hành.

Câu 13: Cho tam giác ABC vuông ở A và hình vuông BCDE. Chứng minh rằng:

AB + AC ≤ CE.

Lời giải:

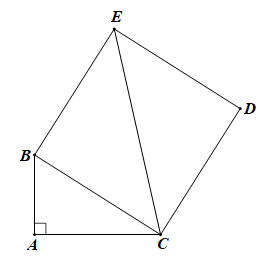
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 2)

Áp dụng định lí Pythagore cho tam giác vuông ABC ta có: AB² + AC² = BC².

Khi đó (AB + AC)² = AB² + AC² + 2.AB.AC = BC² + 2.AB.AC

Áp dụng bất đẳng thức Cosi ta có:

2.AB.AC ≤ AB² + AC² = BC²

⇒ (AB + AC)² ≤ BC² + BC²

Mà BC = BE (do BCDE là hình vuông) và BC² + BE² = CE² (định lí Pythagore cho tam giác vuông BCE)

⇒ (AB + AC)² ≤ BC² + BE² = CE²

⇒ AB + AC ≤ CE

Dấu “=” xảy ra khi AB = AC ⇔ ∆ABC vuông cân ở A.

Câu 14: Chứng minh 5²ⁿ⁻¹.2ⁿ⁺¹ + 3ⁿ⁺¹.2²ⁿ⁻¹ chia hết cho 38.

Lời giải:

Đặt A = 5²ⁿ⁻¹.2ⁿ⁺¹ + 3ⁿ⁺¹.2²ⁿ⁻¹

Với n = 1, ta có B = 5.4 + 9.2 = 38 chia hết cho 38 hay B ⁝ 38.

Giả sử B ⁝ 38 khi n = k, ta cần chứng minh B ⁝ 38 khi n = k + 1.

Đặt a = 5²ⁿ⁻¹.2ⁿ⁺¹; b = 3ⁿ⁺¹.2²ⁿ⁻¹

Ta có: a + b = 38c, c nguyên

Với n = k + 1 thì B = 50a + 12b = 38a + 12(a + b)

Mà 38a ⁝ 38 và a + b ⁝ 38

Suy ra 12(a + b) ⁝ 38

⇒ B ⁝ 38 (đpcm).

Câu 15: Chứng minh nếu n² chia hết cho 9 thì n chia hết cho 3 (với n là số tự nhiên).

Lời giải:

Vì n² chia hết cho 9, ta giả sử n² = 9k (k ∈ ℕ)

Khi đó 9k là số chính phương.

Mà 9 = 3² nên k là số chính phương, do đó tồn tại số m sao cho k = m² (m ∈ ℕ)

Từ n² = 9k ta có $n = 3 \sqrt{k} = 3 m$ nên n chia hết cho 3.

Câu 16: Tìm số thích hợp để điền vào dãy số sau: 3; 17; 59; 185; 563; …

Lời giải:

Đáp án: 1697

Giải thích:

Xét: Hiệu giữa 3 và 17 là 14

Hiệu giữa 17 và 59 là 42 = 14.3

Hiệu giữa 59 và 185 là 126 = 42.3

Hiệu giữa 185và 563 là 378 = 126.3

⇒ Ta có quy luật hiệu của hai số sau sẽ gấp 33 lần hiệu của hai số trước (có lặp lại số ở giữa 22 số kia)

⇒ Số cần điền là: 378.3 + 563 = 1697.

Câu 17: Một khu đô thị hình chữ nhật được vẽ trên bản đồ 1: 30000. Trên bản đồ chiều dài của khu đô thị là 3cm, chiều rộng là 2cm. Tính diện tích thực tế của khu đô thị.

Lời giải:

Diện mảnh đất là:

3 × 2 = 6 (cm²)

Diện tích thật của mảnh đất là:

6 × 30000 = 180 000 (cm²).

Đáp số: 180 000 (cm²).

Câu 18: Thống kê điểm kiểm tra môn Toán của một lớp 10 có 22 học sinh nữ và 20 học sinh nam được cho ở bảng sau:

Điểm thi	0	1	2	3	4	5	6	7	8	9	10
Tần số	3	2	1	1	3	7	4	8	9	3	1

Cho biết đơn vị điều tra và kích thước của mẫu số liệu trên?

A. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 42;

B. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 22;

C. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 20;

D. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 42.

Lời giải:

Đáp án đúng là: D

Đơn vị điều tra: một hsinh lớp 10.

Do lớp học có 22 nữ và 20 nam nên lớp có tất cả 42 học sinh . Do đó; kích thước của mẫu số liệu: 42.

Vậy ta chọn phương án D.

Câu 19: Một đội sản xuất chuẩn bị gạo đủ cho 120 công nhân ăn trong 30 ngày. Nhưng phải nhận thêm công nhân nên số gạo dự trữ chỉ đủ ăn trong 15 ngày. Hỏi sau khi nhận thêm công nhân, đội sản xuất có tất cả bao nhiêu người?

Lời giải:

1 người ăn hết số gạo đó trong số ngày là:

120 × 30 = 3600 (ngày)

Sau khi nhận thêm công nhân, đội sản xuất có tất cả số người là:

3600 : 15 = 240 (người)

Đáp số: 240 người.

Câu 20: Giải phương trình sau: (2x + 3) (x + 2)² (2x + 5) = 315

Lời giải:

(2x + 3) (x + 2)² (2x + 5) = 315

⇔ (4x² +16x + 15)(x² + 4x + 4)= 315

⇔ (4x² + 16x + 15)(4x² + 16x + 16) = 1260

Đặt t = 4x² + 16x + 15 (t ≥ 0). Phương trình đã cho trở thành:

(t − 1)t = 1260

⇔ (t − 36)(t + 35) = 0

⇔ t = 36

⇔ 4x² + 16x + 16 = 36

⇔ (x + 2)² = 3

$\Leftrightarrow [\begin{array}{l} x + 2 = 3 \\ x + 2 = - 3 \end{array}$

Câu 21: Cho a + b + c + d = 0. Chứng minh rằng: a³ + b³ + c³ + d³ = 3.(ab ‒ cd).(c + d).

Lời giải:

Ta có:

a + b + c + d = 0

⇒ a + b = ‒(c + d)

⇒ (a + b)³ = ‒(c + d) ³

⇒ a³ + b³ + 3ab(a + b) = ‒c³ ‒ d³ ‒ 3cd(c + d)

⇒ a³ + b³ + c³+ d³ = ‒3ab(a + b) ‒ 3cd(c + d)

⇒ a³ + b³ + c³ + d³ = 3ab(c + d) ‒ 3cd(c + d) (vì a + b = ‒ (c + d))

⇒ a³ + b³ + c³ + d³ = 3(c + d)(ab ‒ cd) (đpcm).

Câu 22: Cho tam giác ABC có M ∈ BC. Kẻ MN song song với AB (N ∈ AC) và MP // AC (P ∈ AB). Gọi I là trumg điểm của NP. Chứng minh A, I, M thẳng hàng.

Lời giải:

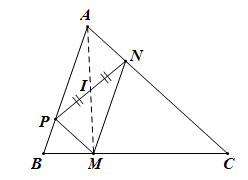
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 3)

Ta có:

NM // AB ⇒ MN // AP

MP // AC ⇒ MP // AN

⇒ Tứ giác APMN là hình bình hành có 2 đường chéo AM và PN.

Mà I là trung điểm của NP

⇒ I cũng là trung điểm của AM hay A, I, M thẳng hàng.

Câu 23: Tìm m để đa thức x³ + y³ + z³ + mxyz chia hết cho đa thức x+ y + z.

Lời giải:

Ta có:

x³ + y³ + z³ + mxyz

= (x + y + z)³ − 3(x + y)(y + z)(x + z) + mxyz

= (x + y + z)³ − 3[xy(x + y) + yz( y+ z) + xz(x + z) + 2xyz] + mxyz

= (x + y + z)³ − 3[xy(x + y + z) + yz(x + y + z) + xz(x + y + z) − xyz] + mxyz

= (x + y + z)³ − 3(x + y + z)(xy + yz + xz) + 3xyz + mxyz

= (x + y + z)(x² + y² + z² − xy − yz − xz) + (m + 3).xyz

Như vậy, để x³ + y³ + z³ + mxyz chia hết cho đa thức x+ y + z ∀x, y, z thì (m + 3)xyz ⋮ (x + y + z), ∀x, y, z

⇒ m + 3 = 0 ⇒ m = −3.

Câu 24: Lớp 10A có 45 học sinh, trong đó 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào trong 3 môn trên và 5 em thích cả 3 môn. Hỏi có bao nhiêu em thích 1 môn trong 3 môn trên?

Lời giải:

Gọi a, b, c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;

x là số học sịnh chỉ thích hai môn là Văn và Toán;

y là số học sịnh chỉ thích hai môn là Sử và Toán;

z là số học sịnh chỉ thích hai môn là Văn và Sử.

Ta có số em thích ít nhất một môn là 45 − 6 = 39

Ta có hệ phương trình:

$\{\begin{cases} a + x + z + 5 = 25 (1) \\ b + y + z + 5 = 18 (2) \\ c + x + y + 5 = 20 (3) \\ x + y + z + a + b + c + 5 = 39 (4) \end{cases}$

Cộng vế với vế (1), (2), (3) ta có:

a + b + c + 2(x + y + z) + 15 = 63 (5)

Từ (4) và (5) ta có:

a + b + c + 2(39 − 5 − a − b − c) + 15 = 63

⇔ a + b + c = 20.

Vậy chỉ có 2020 em thích chỉ một môn trong ba môn trên.

Câu 25: Tìm x, biết: 3x(x ‒ 1) + x ‒ 1 = 0.

Lời giải:

3x(x ‒ 1) + x ‒ 1 = 0

⇒ 3x(x ‒ 1) + (x ‒ 1) = 0

⇒ (3x + 1)(x ‒ 1) = 0

$\Rightarrow [\begin{array}{l} 3 x + 1 = 0 \\ x - 1 = 0 \end{array} \Rightarrow [\begin{array}{l} x = \frac{- 1}{3} \\ x = 1 \end{array}$

Câu 26: Nêu mệnh đề phủ định và xét tính đúng sai của mệnh đề sau:

A: “Với mọi n ∈ ℕ*, (1 + 2 + .... + n) không chia hết cho 11”.

Lời giải:

Mệnh đề sai.

Mệnh đề phủ định là: Với mọi n ∈ ℕ*, (1 + 2 + .... + n) chia hết cho 11.

$P = 1 + 2 + ... + n = \frac{n (n + 1)}{2}$ , n = 11

⇒ P chia hết cho 11.

Vậy tồn tại số tự nhiên n để P chia hết cho 11.

Câu 27: Tính: 1,4 × 10.

Lời giải:

Ta có : 1,4 × 10 = 14.

Câu 28: Cho hàm số (c) có y = f(x) = x² ‒ 2x + 3. Viết phương trình tiếp tuyến với (c) tại điểm thuộc (c) có hoành độ x₀ = 1.

Lời giải:

f′(x) = 2x − 2

Do phương trình tiếp tuyến với (c) tại điểm thuộc (c) có hoành độ x₀ = 1 nên thay x = 1 vào f’(c) ta có: f(1) = 2

Phương trình tiếp tuyến: y = 2.

Câu 29: Có bao nhiêu số tự nhiên có 10 chữ số đôi một khác nhau, trong đó các chữ số 1, 2, 3, 4, 5 được xếp theo thứ tự tăng dần từ trái qua phải và chữ số 6 luôn đứng trước chữ số 5.

Lời giải:

Gỉa sử số cần tìm có 10 chữ số khác nhau tương ứng với 10 vị trí.

Vì chữ số 0 không đứng vị trí đầu tiên nên có 9 cách xếp vị trí cho chữ số 0 .

Có $A_{9}^{3}$ cách xếp các chữ số 7; 8 ;9 vào 9 vị trí còn lại .

Vì chữ số 6 đứng trước chữ số 5 nên có 5 cách xếp vị trí cho chữ số 6 và 1 cách xếp cho các chữ số 1; 2; 3; 4; 5 theo thứ tự tăng dần. Theo quy tắc nhân $9.5. A_{9}^{3} = 22680$ số thoả mãn.

Câu 30: Một đội công nhân 9 người trong một ngày đắp được 60 mét đường. Người ta bổ sung thêm 18 người nữa cùng đắp thì trong một ngày đắp được bao nhiêu mét đường đó (mức đắp mỗi người như nhau)?

Lời giải:

Số người công nhân hiện có là:

9 + 18 = 27 (người)

27 người đắp được số đoạn đường là:

$\frac{27}{9} \times 60 = 180$

Đáp số: 180m.

Câu 31: Một cửa hàng có 480 thùng hàng, mỗi thùng nặng 65kg. Cửa hàng đã bán được 300 thùng hàng. Số thùng hàng còn lại nặng bao nhiêu ki - lô -gam ?

Lời giải:

Số thùng hàng còn lại là:

480 ‒ 300 = 180 (thùng)

Số ki - lô - gam 180 thùng nặng là:

180 × 65 = 11700 (kg)

Đáp số: 11700 kg.

Câu 32: Nhân dịp lễ 20/10, shop thời trang Gumac giảm giá 40% cho các mặt hàng. Lan mua cái đầm hết 297 000 đồng. Tính giá tiền cái đầm trước khi giảm.

Lời giải:

297 000 đồng ứng với số phần trăm giá ban đầu của bộ quần áo là: 100% ‒ 40% = 60%

Giá ban đầu của bộ quần áo là: 297 000 : 60% = 495 000 (đồng)

Đáp số: 495 000 đồng.

Câu 33: Với giá trị nào của x thì đa thức dư trong mỗi phép chia sau có giá trị bằng: (x⁵ + 2x⁴ + 3x⁴ + x ‒ 3) : (x² + 1)

Lời giải:

(x⁵ + 2x⁴ + 3x⁴ + x ‒ 3) : (x² + 1)

$= \frac{x^{5} + x^{3} + 2 x^{4} + 2 x^{2} + 2 x^{3} + 2 x - 2 x {}_{2}- 2 - x - 1}{x^{2} + 1} = x^{3} + 2 x^{2} + 2 x - 2 + \frac{- x - 1}{x^{2} + 1}$

Để số dư là 0 thì ‒x ‒ 1 = 0 ⇔ x = ‒1.

Câu 34: Cho tứ giác ABCD có hai góc đối ở đỉnh B và D cùng bằng 90°. Gọi O là trung điểm của AC. Chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn đường kính AC.

Lời giải:

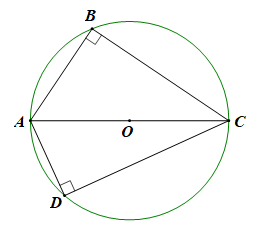
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 4)

Xét ∆ABC có: $\hat{A B C} = 90^{o}$ (gt)

Suy ra AC là cạnh huyền.

Lại có: AO = OC (gt)

⇒ BO là đường trung tuyến ∆ABC

⇒ BO = AO = OC (đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền) (1)

Tương tự ta chứng minh được: DO = AO = OC (2)

Từ (1) và (2) ta có: BO = AO = OC = DO

Suy ra 4 điểm A, B, C, D cùng thuộc đường trong đường kính AC.

Câu 35: Tứ giác có hai góc đối bằng 90° có phải là hình chữ nhật không?

Lời giải:

Tứ giác có 2 góc đối bằng 90° không có nghĩa tứ giác đấy là hình chữ nhật, vì tứ giác có 3 góc bằng 90° mới là hình chữ nhật.

Câu 36: Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số có 5 chữ số khác nhau mà số đó nhất thiết có mặt các chữ số 1, 2, 5?

Lời giải:

Số có 5 chữ số khác nhau mà có 1, 2, 5 thì 2 chữ số còn lại lấy từ 4 chữ số 0, 3, 4, 6.

Lấy 2 số trong 4 số có $C_{2}^{4}$ cách, trong đó có 3 trường hợp gồm 0; 3, 0; 4, 0; 6 .

Ba trường hợp trên giống nhau và có 3.4.4.3.2.1 = 288 số.

Ba trường hợp còn lại giống nhau và có 3.5! = 360 số.

Vậy có tất cả 288 + 360 = 648 số cần tìm.

Câu 37: Từ các số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số có 3 chữ số khác nhau chia hết cho 3.

Lời giải:

Số chia hết cho 3 thì tổng các chữ số của số đó phải chia hết cho 3.

Ta có các bộ ba có tổng chia hết cho 3 là: (1; 2; 3), (1; 2; 6), (1; 3; 5), (1; 5; 6), (2; 3; 4), (2; 4; 6), (3; 4; 5), (4; 5; 6).

Mỗi bộ ba có 3! cách sắp xếp để được một số chia hết cho 3.

Vậy số các số có 3 chữ số khác nhau được lập từ các chữ số: 1; 2; 3; 4; 5; 6 chia hết cho 3 là: 8.3! = 48 (số).

Câu 38: Cho định lí “Cho số tự nhiên n, nếu n⁵ chia hết cho 5 thì n chia hết cho 5”.

Định lí này được viết dưới dạng P ⇒ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.

Lời giải:

– Định lý đảo: Cho số tự nhiên n, nếu n chia hết cho 5 thì n⁵ chia hết cho 5.

– Cho số tự nhiên n, n⁵ chia hết cho 5 là điều kiện cần và đủ để n chia hết cho 5.

Câu 39: Viết các số (0,25)⁸ và (0,125)⁴ dưới dạng các lũy thừa với cơ số 0,5.

Lời giải:

Ta có:

(0,25)⁸ = [(0,5)²]⁸ = (0,5)^2.8 = (0,5)¹⁶

(0,125)⁴ = [(0,5)³]⁴ = (0,5)^3.4 = (0,5)¹²

Câu 40: Tính hợp lý: (10²+ 11²+ 12²) : (13²+ 14²).

Lời giải:

(10²+ 11²+ 12²) : (13²+ 14²)

= (10 × 10 + 11 × 11 + 12 × 12) : (13²+ 14²)

= [(12 + 1)² + (12 + 2)²] : (13²+ 14²)

= (13²+ 14²) : (13²+ 14²)

= 1

Câu 41: Tìm nghiệm nguyên của phương trình: y² = x(x + 1)(x + 7)(x + 8).

Lời giải:

y² = x(x + 1)(x + 7)(x + 8) ⟺ y² = (x² + 8x)( x² + 8x + 7)

Đặt t = x² + 8x, ta có: y² = t(t + 7) = t²+ 7t

⟺ 4y² = 4t² + 28t + 49 – 49

⟺ (2t + 7)² – 4y² = 49

⟺ (2t + 7 – 2y)(2t + 7 + 2y) = 49 = 7.7

$\Leftrightarrow [\begin{array}{l} 2 t + 7 - 2 y = 7 \\ 2 t + 7 + 2 y = 7 \end{array} \Leftrightarrow [\begin{array}{l} 2 x^{2} + 16 x + 7 - 2 y = 7 \\ 2 x^{2} + 16 x + 7 + 2 y = 7 \end{array} \Leftrightarrow [\begin{array}{l} 2 x^{2} + 16 x - 2 y = 0 \\ 2 x^{2} + 16 x + 2 y = 0 \end{array}$

Vậy nghiệm của phương trình là: (–8; 0), (0; 0).

Câu 42: Đố bạn chỉ với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau) mà xếp được thành 6 tam giác đều.

Lời giải:

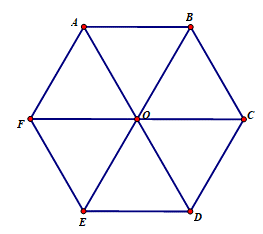
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 5)

Với 12 que diêm (hay 12 chiếc que có độ dài bằng nhau), ta có thể xếp chúng thành hình lục giác đều với các đường chéo chính cắt nhau như hình trên, ta được 6 hình tam giác đều.

Câu 43: Cho n là số tự nhiên. Chứng minh: 5²ⁿ⁺¹ + 2ⁿ⁺⁴ +2ⁿ⁺¹ chia hết cho 23.

Lời giải:

Ta có:

5²ⁿ⁺¹ + 2ⁿ⁺⁴ +2ⁿ⁺¹

= 5.5²ⁿ + 2⁴.2ⁿ + 2.2ⁿ

= 5.25ⁿ+ 18.2ⁿ

= 5.25ⁿ+ 23.2ⁿ – 5.2ⁿ

= 23.2ⁿ + 5(25ⁿ – 2ⁿ)

Ta có 25ⁿ – 2ⁿ ⋮ (25 – 2)

⇒ 25ⁿ – 2ⁿ ⋮ 23

⇒ 5(25ⁿ – 2ⁿ) ⋮ 23

Vì 23 ⋮ 23 ⇒ 23. 2ⁿ ⋮ 23

Vậy 23. 2ⁿ + 5(25ⁿ – 2ⁿ) ⋮ 23 ⇒ 5²ⁿ⁺¹ + 2ⁿ⁺⁴ +2^n:1⋮ 23.

Câu 44: Cho nửa hình tròn H như hình vẽ, đường kính hình tròn là 12cm.

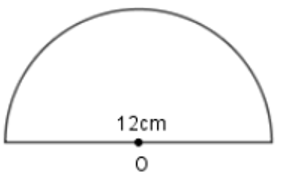
Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 6)

Chu vi hình H là:

A. 18,84 cm;

B. 30,84 cm;

C. 37,68 cm;

D. 49,68 cm.

Lời giải:

Đáp án đúng là: B

Chu vi hình tròn tâm O là: 12 × 3,14 = 37,68 (cm)

Nửa chu vi của hình tròn tâm O là: 37,68 : 2 = 18,84 (cm)

Chu vi hình H là: 18,84 + 12 = 30,84 (cm)

Đáp số: 30,84 cm.

Vậy đáp án đúng là: B

Câu 45: Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?

A. 1470;

B. 750;

C. 2940;

D. 1500.

Lời giải:

Đáp án đúng là: D

Sắp xếp cụm số 3,4,5 có 2 cách sắp xếp là 345 và 543

TH1: Cụm 2 số 3,4,5 đứng đầu có: 2.7.6.5 = 240 số thỏa mãn

TH2: Cụm 3 số 3,4,5 không đứng đầu có 3 cách sắp xếp là: x345xx; xx345x; xxx345

3 chữ số còn lại có: 6.6.5 = 180 cách chọn và sắp xếp

Do đó có 2.3.180 = 1080 số thỏa mãn

Theo quy tắc cộng có:

420 + 1080 = 1500 số thỏa mãn yêu cầu bài toán

Vậy đáp án đúng là đáp án D.

Câu 46: Một kho gạo có 60 tấn gạo tẻ và gạo nếp trong đó số gạo nếp bằng $\frac{3}{7}$ số gạo tẻ. Tính số gạo nếp, gạo tẻ có trong kho?

Lời giải:

Tổng số phần bằng nhau là : 3 + 7 =10 (phần)

Giá trị 1 phần là : 60 : 10 = 6 (tấn)

Số gạo tẻ có trong kho là : 6 × 7 = 42 (tấn)

Số gạo nếp có trong kho là: 6 × 3 = 18 (tấn)

Đáp số: 42 tấn gạo tẻ, 18 tấn gạo nếp

Câu 47: Một cỗ bài có 52 quân, mỗi chất cơ, rô, nhép, bích đều có 13 quân. Có bao nhiêu cách lấy ra 5 quân sao cho có đủ cả 4 chất: cơ, rô, nhép, bích?

Lời giải:

Để lấy 5 quân mà được 4 chất khác nhau thì có số cách lấy là: $C_{5}^{1} C_{13}^{1} . C_{4}^{1} . C_{13}^{1} . C_{3}^{1} . C_{13}^{1} . C_{2}^{1} . C_{13}^{1} . C_{1}^{1} . C_{12}^{1}$

Câu 48: Tháng 2 năm nào đó có 5 ngày thứ Năm. Hỏi ngày 1 tháng đó là thứ mấy? Chủ nhật tháng đó vào những ngày nào?

Lời giải:

Vì tháng 2 chỉ có 28 ngày hoặc 29 ngày mà lại có đến 5 ngày là thứ năm nên có 4 tuần kể từ thứ năm đầu đến thứ năm cuối.

Suy ra từ thứ năm đầu tiên đến thứ năm cuối cùng có số ngày là: 4 × 7 + 1 = 29 (ngày)

Như vậy 29 ngày kể từ thứ năm đầu tiên đến thứ năm cuối cùng phải trùng hoàn toàn với 29 ngày trong tháng nên ngày thứ năm đầu tiên của tháng đó là mùng 1 và ngày 29 tháng đó cũng là thứ năm.

Do đó ngày chủ nhật đầu tiên của tháng đó là ngày mùng 4. Các ngày chủ nhật của tháng đó là: 04 ; 11 ; 18 ; 25.

Câu 49: Cho 3 điểm A, B, C bất kì và một điểm O khác điểm A, B, C. Có bao nhiêu tia gốc O và đi qua một trong 3 điểm A, B, C.

Lời giải:

Các tia có gốc là O và đi qua một trong 3 điểm A, B, C là: OA, OB, OC.

Vậy có 3 tia thỏa mãn yêu cầu.

Câu 50: Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 9 cm, CH = 16 cm. Tính độ dài các cạnh AB, AC và chiều dài AH.

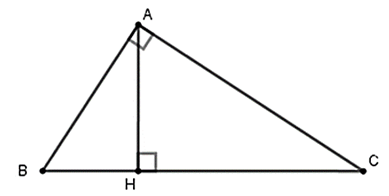Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 66) (ảnh 7) Lời giải: